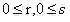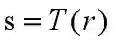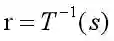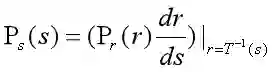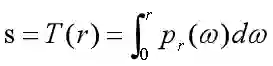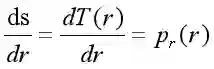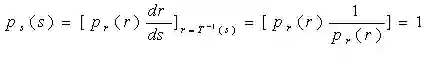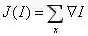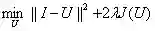实战 | 用Python做图像处理（三）

2018 年 5 月 29 日 七月在线实验室

图像的缩放、均匀操作、直方图均衡化及降噪

▌图像的缩放

Numpy的数组对象是我们处理图像和数据的主要工具。想要对图像进行缩放处理没有现成的简单的方法。因此我们使用如下代码实现图像的缩放：

from PIL import Image
from numpy import *
from pylab import *


def imresize(im, sz):
    pil_im = Image.fromarray(uint8(im))
    return array(pil_im.resize(sz))

im = Image.open("test.jpg")
im1 = imresize(im, (128, 128))

figure()
gray()

subplot(1, 2, 1)
imshow(im)

subplot(1, 2, 2)
imshow(im1)
title("Zoom picture")

show()

输出的结果如下图所示：

这其中，我们定义了一个imresize()函数，使用PIL对象重新定义图像数组的大小，其中，fromarray()方法进行反相操作,uint8:将其他数据类型转换为uint8

▌图像均匀

图像均匀操作是减少图像噪声的一种简单方式，通常用于艺术特效，我们可以简单的从图像列表中计算出一幅平均图像，假设所有的图像具有相同的大小，我们可以将这些图像简单的相加，然后除以图像的数目，来计算平均图像，下面的函数可以用来计算平均图像：

def compute_average(imlist):
    averageim = array(Image.open(imlist[0]), 'f')
    for imname in imlist[1:]:
        try:
            averageim += array(Image.open(imname))
        except:
            print(imname + '...skipped')
    averageim /= len(imlist)
return array(averageim, 'unit8')

这个函数中包含了一些基本的异常处理技巧，可以自动跳过不能打开的图像，我们还可以使用mean()函数计算平均图像。mean()函数需要将所有的图像堆积到一个数组中；也就是说，如果有很多幅图像，该处理方式会占用大量内存。

完整的代码为：

from PIL import Image
import numpy as np
from pylab import *
import matplotlib.pyplot as plt
import os
def compute_average(imlist):
    """计算图像列表的平均像素"""
    # 打开第一幅图像，将其存储在浮点型数组中
    averageim = array(Image.open(imlist[0]), 'f')
    for imname in imlist[1:]:
        try:
            averageim += array(Image.open(imname))
        except:
            print
            imname + "...skipped"
        averageim /= len(imlist)
    return array(averageim, 'uint8')
if __name__ == "__main__":
    dirs = os.listdir("/home/xuna/桌面/image")
    imlist = []
    for name in dirs:
        name = "/home/xuna/桌面/image/" + name
        imlist.append(name)
    print
    imlist
    im = compute_average(imlist)
    imshow(im)
    show()

▌直方图均衡化

图像灰度变换中有一个非常有用的例子就是直方图均衡化。由之前的灰度图像的直方图可以看出，一般情况下，图像上某些灰度值较多，有些灰度值较少，直方图均衡化为的是使灰度值较为均衡。那么为什么要进行图像均衡化呢？是因为均衡化的图像能够提高对比度和灰度色调的变化，使图像更加清晰。均衡化的图像意味着它的像素占有很多的灰度级而且分布均匀，它往往有高对比度和多变的灰度色调。

从图片本身的角度看，直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同，把给定图像的直方图分布改变成“均匀”分布直方图分布。

那么如何进行图像均衡化呢？对于任意一副灰度分布不均匀的图像，为了使图像直方图信息自动达到均匀分布，我们需要引入一个变换函数。这个变换函数的基本思想是对图像中像素个数多的灰度级进行展宽，而对图像中像素个数少的灰度进行压缩，即将一幅图像的灰度直方图变平，使变换后的图像中每个灰度值的分布概率都相同从而扩展像元取值的动态范围。

这个变换函数通常是图像中像素值的累积分布函数(cumulativate distribution function，简写为cdf，将像素值的范围映射到目标范围的归一化操作)，累积函数和概率论中的累积分布函数类似。例如对于还有5个数的序列[1,2,3,4,5],其累积函数含有5个数，第一个数是1，第二个是1+2=3，……，第五个数是1+2+3+4+5=15，所以其累积函数是[1,3,6,10,15]。需要注意的是，不论像素无论怎么映射，一定要保证原来的大小关系不变，较亮的区域，依旧是较亮的，较暗依旧暗，只是对比度增大，绝对不能明暗颠倒。

直方图变换其实是一种灰度变换，灰度变换的变换函数决定了输入随机变量与输出随机变量之间的关系，也就是两个随机变量的关系；一副图像是二维离散的数据，不利于使用数学的工具进行处理，在数字图像处理中，我们通常是采用连续的变量进行推导，最后在推广到离散的情况。

在对图像做进一步处理之前，直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法，并且可以增强图像的对比度。

我们用r和s分别表示原图像灰度级和经直方图均衡化之后的图像灰度级，为了方便我们讨论，我们首先要做的事便是对s和r的归一化处理，使得：

对于一幅给定的图像，归一化之后灰度级分布在范围内。对[0,1]区间内任一个r至进行如下变换：

我们令从s到r的反变换为：

r的概率密度为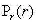，s的概率密度为：

我们令变换函数为:

该函数就称为r的累积分布函数，对式中r求导有：

把结果带入前式：

由此可见，变换后变量s在其定义域内的概率密度是均匀分布的，用r的累积分布函数做变换函数，可以产生一幅灰度级分布具有均匀概率密度的图像，这个结果扩展了像素取值的动态范围。

我们把直方图均衡化的过程封装在一个函数里面，函数名字叫做histeq，输入原图像矩阵和直方图分块数，输出均衡化后的图像矩阵和累积函数。

具体的代码如下：

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib.cm as cm

def histeq(image_array, image_bins=256):
    # 将图像矩阵转化成直方图数据，返回元组(频数，直方图区间坐标)
    image_array2, bins = np.histogram(image_array.flatten(), image_bins)
    # 计算直方图的累积函数
    cdf = image_array2.cumsum()
    # 将累积函数转化到区间[0,255]
    cdf = (255.0 / cdf[-1]) * cdf
    # 原图像矩阵利用累积函数进行转化，插值过程
    image2_array = np.interp(image_array.flatten(), bins[:-1], cdf)
    # 返回均衡化后的图像矩阵和累积函数
    return image2_array.reshape(image_array.shape), cdf
image = Image.open("test.jpg").convert("L")
image_array = np.array(image)

fig = plt.figure(figsize=(15, 15))
ax = fig.add_subplot(2, 2, 1)
ax.hist(image_array.flatten(), 256)
plt.subplot(2, 2, 2)
plt.imshow(image_array, cmap=cm.gray)
plt.axis("off")

a = histeq(image_array)  # 利用刚定义的直方图均衡化函数对图像进行均衡化处理
plt.subplot(2, 2, 3)
plt.hist(a[0].flatten(), 256)
plt.subplot(2, 2, 4)
plt.imshow(Image.fromarray(a[0]), cmap=cm.gray)
plt.axis("off")

plt.show()

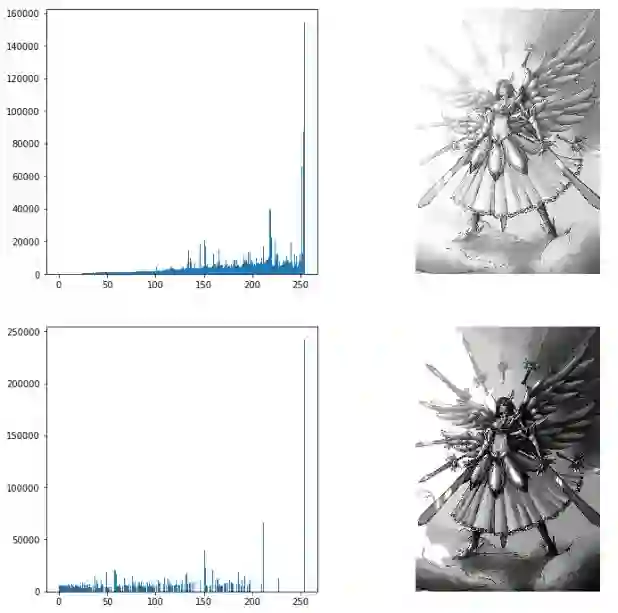
输出结果为：

比较上面输出的均衡化之前和均衡化之后的两幅直方图，我们可以清晰的看出直方图均衡化后的图像对比度增强了，原先图像灰色区域的细节变得更加清晰。

▌图像降噪

图像去噪是给定一幅受损图像，在去除图像噪声的同时，尽可能地保留图像细节和结构的处理技术。图像去噪对于很多应用来说都非常重要；这些应用范围很广，小到让你的照片看起来更漂亮，大到提高卫星图像的质量。我们这里使用ROF去噪模型，ROF模型具有很好的性质；使处理后的图像更加平滑，同时保留图像边缘和结构信息。

ROF模型的数学基础和处理技巧非常高深，有兴趣的读者可以自学深入了解，本文只是做一个简单介绍。

▌ROF模型

一副图像I的全变差（Total Variation,TV）定义为梯度范数之和。

在连续表示的情况下，全变差表示为：

在离散表示的情况下，全变差表示为：

其中，上面的式子是在所有图像坐标x=[x,y]上取和。

在ROF模型里，目标函数是为了寻找降噪后的图像U，使下式最小：

其中范数||I-U||是去噪后图像U和原始图像I差异的度量。也就是说，本质上该模型使去噪后的图像像素值“平坦变化”，但是在图像区域的边缘上，允许图像像素值“跳跃变化”。

代码如下：

from numpy import *
from numpy import linalg as LA
from numpy import random
from scipy.ndimage import filters
from scipy.misc import imsave
from PIL import Image


def denoise(im, U_init, tolerance=0.1, tau=0.125, tv_weight=100):
    m, n = im.shape  # 噪声图像的大小
    U = U_init
    Px = im  # 对偶域的x 分量
    Py = im  # 对偶域的y 分量
    error = 1

    while (error > tolerance):
        Uold = U

        # 原始变量的梯度
        GradUx = roll(U, -1, axis=1) - U  # 变量U 梯度的x 分量
        GradUy = roll(U, -1, axis=0) - U  # 变量U 梯度的y 分量

        # 更新对偶变量  
        PxNew = Px + (tau / tv_weight) * GradUx
        PyNew = Py + (tau / tv_weight) * GradUy
        NormNew = maximum(1, sqrt(PxNew ** 2 + PyNew ** 2))

        Px = PxNew / NormNew  # 更新x 分量（对偶）
        Py = PyNew / NormNew  # 更新y 分量（对偶）

        # 更新原始变量
        RxPx = roll(Px, 1, axis=1)
        RyPy = roll(Py, 1, axis=0)

        DivP = (Px - RxPx) + (Py - RyPy)  # 对偶域的散度
        U = im + tv_weight * DivP  # 更新原始变量

        # 更新误差
        error = linalg.norm(U - Uold) / sqrt(n * m)
    return U, im - U


im = zeros((500, 500))
im[100:400, 100:400] = 128
im[200:300, 200:300] = 255
im = im + 30 * random.standard_normal((500, 500))

U, T = denoise(im, im)
G = filters.gaussian_filter(im, 10)

from scipy.misc import imsave

imsave('test1.pdf', U)
imsave('test2.pdf', G)

输出结果如下：

（a）

（b）

图中（a）为经过高斯模糊的图像，（b）为经过ROF模型去噪后的图像

在上面代码中，输入为含有噪声的灰度图像、U 的初始值、TV 正则项权值、步长、停业条件；输出：去噪和去除纹理后的图像、纹理残留。im.shape表示噪声图像的大小；Px和Py分别表示对偶域的x分量和对偶域的y分量；GtandUx和GrandUy分别表示变量U梯度的x分量和y分量； RxPx = roll(Px,1,axis=1)和 RyPy = roll(Py,1,axis=0)分别表示对x 分量进行向右x 轴平移和对y 分量进行向右y 轴平移；denoise方法最终返回去早后的图像和纹理残余。

在这个例子中，我们使用了roll() 函数。顾名思义，在一个坐标轴上，它循环“滚动”数组中的元素值。该函数可以非常方便地计算邻域元素的差异，比如这里的导数。我们还使用了linalg.norm() 函数，该函数可以衡量两个数组间（这个例子中是指图像矩阵U 和Uold）的差异。

下面，我们使用Erza Scarlet的图像进行去噪的实战练习

代码如下：

from numpy import *
from numpy import linalg as LA
from numpy import random
from scipy.ndimage import filters
from scipy.misc import imsave
from PIL import Image
import matplotlib.pyplot as plt


def denoise(im, U_init, tolerance=0.1, tau=0.125, tv_weight=100):
    m, n = im.shape  # 噪声图像的大小
    U = U_init
    Px = im  # 对偶域的x 分量
    Py = im  # 对偶域的y 分量
    error = 1

    while (error > tolerance):
        Uold = U

        GradUx = roll(U, -1, axis=1) - U  # 变量U 梯度的x 分量
        GradUy = roll(U, -1, axis=0) - U  # 变量U 梯度的y 分量

        PxNew = Px + (tau / tv_weight) * GradUx
        PyNew = Py + (tau / tv_weight) * GradUy
        NormNew = maximum(1, sqrt(PxNew ** 2 + PyNew ** 2))

        Px = PxNew / NormNew  # 更新x 分量（对偶）
        Py = PyNew / NormNew  # 更新y 分量（对偶）

        RxPx = roll(Px, 1, axis=1)  # 对x 分量进行向右x 轴平移
        RyPy = roll(Py, 1, axis=0)  # 对y 分量进行向右y 轴平移

        DivP = (Px - RxPx) + (Py - RyPy)  # 对偶域的散度
        U = im + tv_weight * DivP  # 更新原始变量

        # 更新误差
        error = linalg.norm(U - Uold) / sqrt(n * m)
    return U, im - U


fig = plt.figure(figsize=(15, 15))
im = array(Image.open('test.jpg').convert('L'))
U, T = denoise(im, im)
plt.imshow(U, plt.cm.gray)
plt.axis('equal')
plt.axis("off")
plt.show()

输出如下：

参考：《python计算机视觉编程》http://yongyuan.name/pcvwithpython/

《机器学习第九期》从零到机器学习实战项目，提供GPU&CPU双云平台，作业考试1V1批改（优秀学员内推BAT等）；点击文末“阅读原文”了解详情

登录查看更多

相关内容

关注 0

IM：IFIP/IEEE International Symposium on Integrated Network Management。 Explanation：综合网络管理国际研讨会。 Publisher：IFIP/IEEE SIT： http://dblp.uni-trier.de/db/conf/im/index.html

【2020新书】实战R语言4，323页pdf

专知会员服务

100+阅读 · 2020年7月1日

【实用书】Python技术手册，第三版767页pdf

专知会员服务

234+阅读 · 2020年5月21日