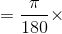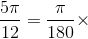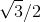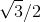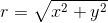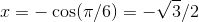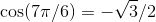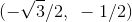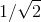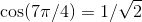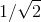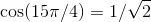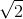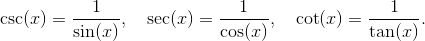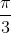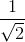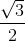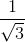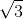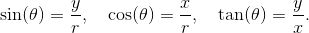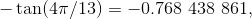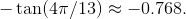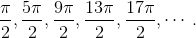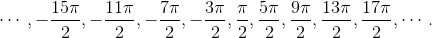三角学回顾01 - 普林斯顿微积分读本

会员服务 ·

三角学回顾01 - 普林斯顿微积分读本

2018 年 9 月 14 日 遇见数学

微积分是一门研究变化的学问

本书不仅让学生们能有效地学习微积分，更重要的是提供了战胜微积分的可靠工具。

下文节选自《普林斯顿微积分读本》, 已获出版社授权许可, [遇见数学] 特此表示感谢!

学习微积分必须要了解三角学. 说实话, 我们一开始不会碰到很多有关三角学的内容, 但当它们出现的时候, 会让我们感觉不容易. 因此, 我们不妨针对三角学最重要的一些方面进行一次全面的回顾：

用弧度度量的角与三角函数的基本知识;
实轴上的三角函数 (不只是介于 0° 和 90° 的角);
三角函数的图像;
三角恒等式.

准备开始回忆吧 ……

2.1　基本知识

首先要回忆的是弧度的概念. 旋转一周, 我们说成 2π 弧度而不是 360°. 这似乎有点古怪, 但这里也有一个理由, 那就是半径为 1 个单位的圆的周长是 2π 个单位. 事实上, 这个圆的一个扇形的弧长就是这个扇形的圆心角的弧度, 如图 2-1 所示.

图　2-1

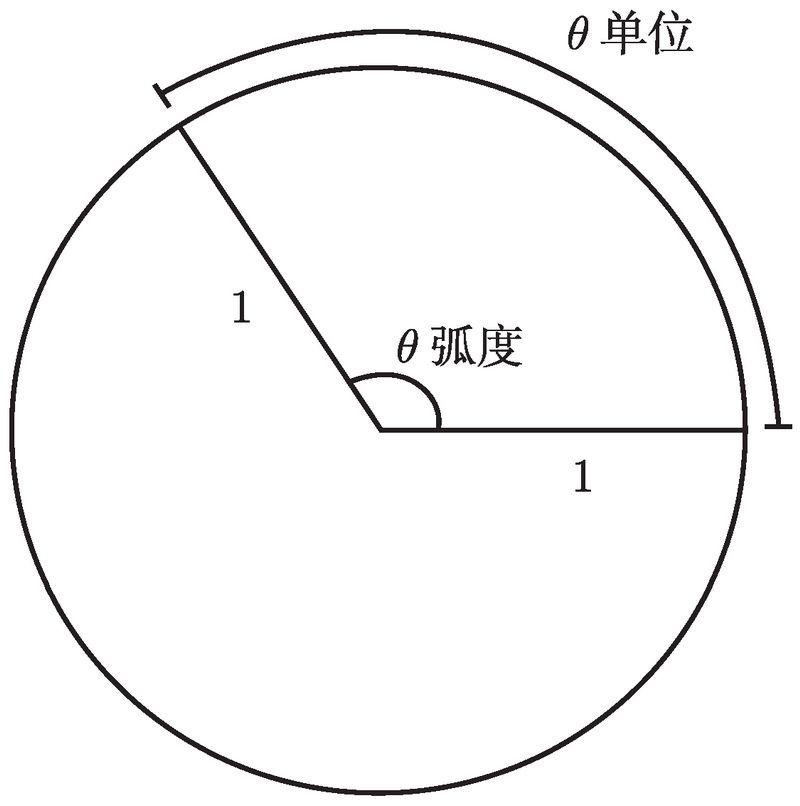
上图表示了一般情况, 但要紧的还是一些常用角的度和弧度表达. 首先, 你应该确实掌握, 90° 和 π/2 弧度是一样的. 类似地, 180° 和 π 弧度是一样的, 270° 和 3π/2 弧度是一样的. 一旦掌握了这几个角, 就试着将图 2-2 中所有的角在度与弧度之间来回转换吧.

图　2-2

更一般地, 如果需要的话, 也可以使用公式

用弧度度量的角用度度量的角.

　例如, 要想知道 5π/12 弧度是多少度, 可求解

用度计量的角,

你会发现 5π/12 弧度就是 (180/π) × (5π/12) = 75°. 事实上, 可以将弧度和度的转换看成是一种单位的转换, 如英里和公里的转换一样. 转换因数就是 π 弧度等于 180°.

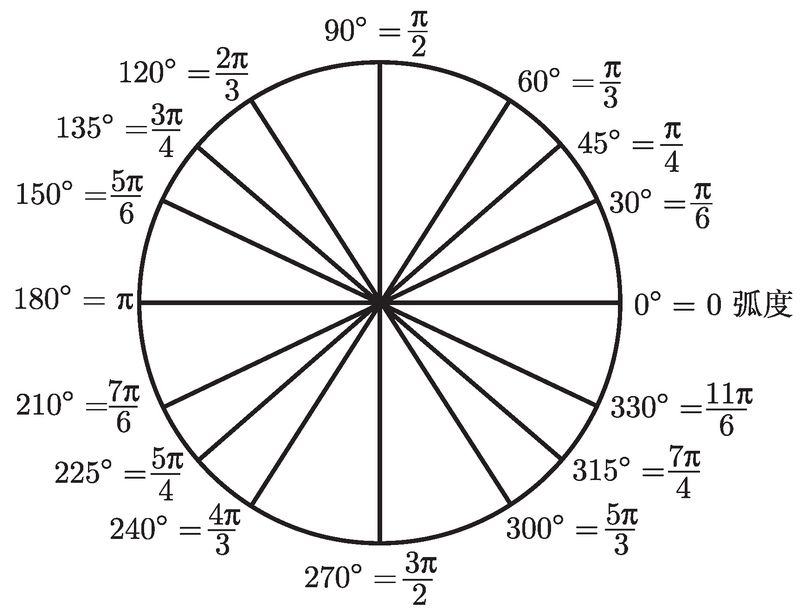
到目前为止, 我们仅仅研究了角, 现在来看看三角函数吧. 显然, 你必须知道如何由三角形来定义三角函数. 假设我们有一个直角三角形, 除直角外的一角被记为 θ, 如图 2-3 所示. 那么, 基本公式为

sin (θ) = ,　cos (θ) = ,　tan (θ) = .

图　2-3

当然, 如果变换了角 θ, 那么也必须变换其对边和邻边, 如图 2-4 所示. 毫不奇怪, 对边就是对着角 θ 的边, 而邻边则是挨着角 θ 的边. 不过, 斜边始终保持不变：它是最长的那条边, 并始终对着直角.

图　2-4

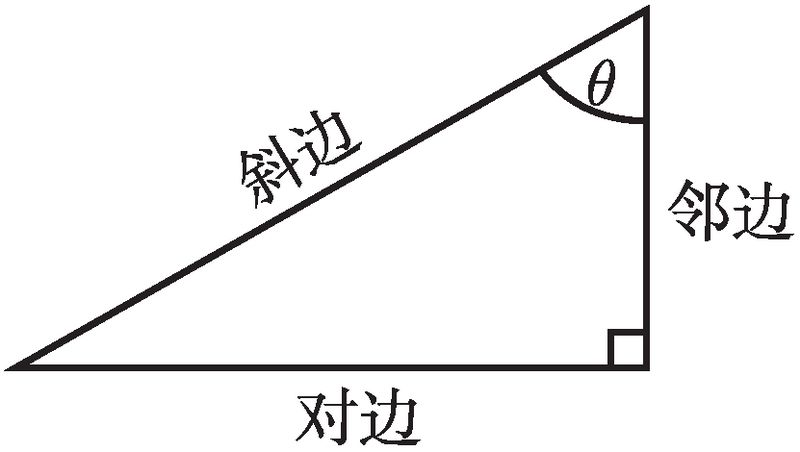
我们也会用到余割、正割和余切这些倒数函数, 它们的定义分别为

　如果你有计划要参加一次微积分的考试 (或者即便你没有), 我的一点建议是：请熟记常用角 0, π/6, π/4, π/3, π/2 的三角函数值. 例如, 你能不假思索化简 sin (π/3) 吗？tan (π/4) 呢？如果你不能, 那么最好的情况下, 你通过画三角形来寻找答案, 从而白白浪费时间; 而最坏的情况下, 由于总是没有化简你的回答, 你白白丢掉分数。解决的方法就是要熟记下表.

	0
sin	0		1
cos	1		0
tan	0	1	★

表中的星号表示 tan (π/2) 无定义. 事实上, 正切函数在 π/2 处有一条垂直渐近线 (从图像上看会很清楚, 我们将在 2.3 节对此进行研究). 无论如何, 你必须能够熟练地说出该表中的任意一项, 而且来回都要掌握! 这意味着你必须能够回答两类问题. 这两类问题的例子是：

(1) sin (π/3) 是什么？(使用该表, 答案是 . )

(2) 介于 0 到 π/2, 其正弦值为的角是什么？(显然, 答案是 π/3. )

当然, 你必须能够回答该表中的每一项所对应的这两类问题. 就算我求大家了, 请背熟这张表! 数学不是死记硬背, 但有些内容是值得记忆的, 而这张表一定位列其中. 因此, 无论是制作记忆卡片, 让你的朋友来测验你, 还是每天抽一分钟记忆, 不管用什么办法, 请背熟这张表.

向上滑动阅览简介及目录

作者者：阿德里安·班纳
译者者：杨爽 , 赵晓婷 , 高璞
出版社：人邮出版社图灵数学

二维码或点击【阅读原文】
跳转遇见微店购买, 然后可领取50-15非图书类优惠券

本书阐述了求解微积分的技巧，详细讲解了微积分基础、极限、连续、微分、导数的应用、积分、无穷级数、泰勒级数与幂级数等内容，旨在教会读者如何思考问题从而找到解题所需的知识点，着重训练大家自己解答问题的能力。

本书适用于大学低年级学生、高中高年级学生、想学习微积分的数学爱好者以及广大数学教师。本书既可作为教材、习题集，也可作为学习指南，同时还有利于教师备课。

第1章函数、图像和直线
1.1 函数
1.1.1 区间表示法
1.1.2 求定义域
1.1.3 利用图像求值域
1.1.4 垂线检验
1.2 反函数
1.2.1 水平线检验
1.2.2 求反函数
1.2.3 限制定义域
1.2.4 反函数的反函数
1.3 函数的复合
1.4 奇函数和偶函数
1.5 线性函数的图像
1.6 常见函数及其图像
第2 章三角学回顾
2.1 基本知识
2.2 扩展三角函数定义域
2.2.1 ASTC方法
2.2.2 （0，2π）以外的三角函数
2.3 三角函数的图像
2.4 三角恒等式
第3 章极限导论
3.1 极限：基本思想
3.2 左极限与右极限
3.3 何时不存在极限
3.4 在∞和—∞处的极限
3.5 关于渐近线的两个常见误解
3.6 三明治定理
3.7 极限的基本类型小结
第4 章求解多项式的极限问题
4.1 x→a时的有理函数的极限
4.2 x→a时的平方根的极限
4.3 x→∞时的有理函数的极限
4.4 x→∞时的多项式型函数的极限
4.5 x→—∞时的有理函数的极限
4.6 包含绝对值的函数的极限
第5 章连续性和可导性
5.1 连续性
5.1.1 在一点处连续
5.1.2 在一个区间上连续
5.1.3 连续函数的一些例子
5.1.4 介值定理
5.1.5 一个更难的介值定理
例子
5.1.6 连续函数的最大值和
最小值
5.2 可导性
5.2.1 平均速率
5.2.2 位移和速度
5.2.3 瞬时速度
5.2.4 速度的图像阐释
5.2.5 切线
5.2.6 导函数
5.2.7 作为极限比的导数
5.2.8 线性函数的导数
5.2.9 二阶导数和更高阶导数
5.2.10 何时导数不存在
5.2.11 可导性和连续性
第6 章求解微分问题
6.1 使用定义求导
6.2 用更好的办法求导
6.2.1 函数的常数倍
6.2.2 函数和与函数差
6.2.3 通过乘积法则求积函数的导数
6.2.4 通过商法则求商函数的导数
6.2.5 通过链式求导法则求复合函数的导数
6.2.6 那个难以处理的例子
6.2.7 乘积法则和链式求导法则的理由
6.3 求切线方程
6.4 速度和加速度
6.5 导数伪装的极限
6.6 分段函数的导数
6.7 直接画出导函数的图像
第7 章三角函数的极限和导数
7.1 三角函数的极限
7.1.1 小数的情况
7.1.2 问题的求解——小数的情况
7.1.3 大数的情况
7.1.4 其他的"情况
7.1.5 一个重要极限的证明
7.2 三角函数的导数
7.2.1 求三角函数导数的例子
7.2.2 简谐运动
7.2.3 一个有趣的函数
第8 章隐函数求导和相关变化率
8.1 隐函数求导
8.1.1 技巧和例子
8.1.2 隐函数求二阶导
8.2 相关变化率
8.2.1 一个简单的例子
8.2.2 一个稍难的例子
8.2.3 一个更难的例子
8.2.4 一个非常难的例子
第9 章指数函数和对数函数
9.1 基础知识
9.1.1 指数函数的回顾
9.1.2 对数函数的回顾
9.1.3 对数函数、指数函数及反函数
9.1.4 对数法则
9.2 e的定义
9.2.1 一个有关复利的问题
9.2.2 问题的答案
9.2.3 更多关于e和对数函数的内容
9.3 对数函数和指数函数求导
9.4 求解指数函数或对数函数的极限
9.4.1 涉及e的定义的极限
9.4.2 指数函数在0附近的行为
9.4.3 对数函数在1附近的行为
9.4.4 指数函数在∞或—∞附近的行为
9.4.5 对数函数在∞附近的行为
9.4.6 对数函数在0附近的行为
9.5 取对数求导法
9.6 指数增长和指数衰变
9.6.1 指数增长
9.6.2 指数衰变
9.7 双曲函数
第10 章反函数和反三角函数
10.1 导数和反函数
10.1.1 使用导数证明反函数存在
10.1.2 导数和反函数：可能出现的问题
10.1.3 求反函数的导数
10.1.4 一个综合性例子
10.2 反三角函数
10.2.1 反正弦函数
10.2.2 反余弦函数
10.2.3 反正切函数
10.2.4 反正割函数
10.2.5 反余割函数和反余切函数
10.2.6 计算反三角函数
10.3 反双曲函数
第11 章导数和图像
11.1 函数的极值
11.1.1 全局极值和局部极值
11.1.2 极值定理
11.1.3 求全局最大值和最小值
11.2 罗尔定理
11.3 中值定理
11.4 二阶导数和图像
11.5 对导数为零点的分类
11.5.1 使用一次导数
11.5.2 使用二阶导数
第12 章绘制函数图像
12.1 建立符号表格
12.1.1 建立一阶导数的符号表格
12.1.2 建立二阶导数的符号表格
12.2 绘制函数图像的全面方法
12.3 例题
12.3.1 一个不使用导数的例子
12.3.2 完整的方法：例一
12.3.3 完整的方法：例二
12.3.4 完整的方法：例三
12.3.5 完整的方法：例四
第13 章最优化和线性化
13.1 最优化
13.1.1 一个简单的最优化例子
13.1.2 最优化问题：一般方法
13.1.3 一个最优化的例子
13.1.4 另一个最优化的例子
13.1.5 在最优化问题中使用隐函数求导
13.1.6 一个较难的最优化例子
13.2 线性化
13.2.1 线性化问题：一般方法
13.2.2 微分
13.2.3 线性化的总结和例子
13.2.4 近似中的误差
13.3 牛顿法
第14 章洛必达法则及极限问题总结
14.1 洛必达法则
14.1.1 类型A：0／0
14.1.2 类型A：±∞／±∞
14.1.3 类型B1：（∞—∞）
14.1.4 类型B2：（0x±∞）
14.1.5 类型C：1±∞，00或∞0
14.1.6 洛必达法则类型的总结
14.2 关于极限的总结
第15 章积分
15.1 求和符号
15.1.1 一个有用的求和
15.1.2 伸缩求和法
15.2 位移和面积
15.2.1 三个简单的例子
15.2.2 一段更常规的旅行
15.2.3 有向面积
15.2.4 连续的速度
15.2.5 两个特别的估算
第16 章定积分
16.1 基本思想
16.2 定积分的定义
16.3 定积分的性质
16.4 求面积
16.4.1 求通常的面积
16.4.2 求解两条曲线之间的面积
16.4.3 求曲线与y轴所围成的面积
16.5 估算积分
16.6 积分的平均值和中值定理
16.7 不可积的函数
第17 章微积分基本定理
17.1 用其他函数的积分来表示的函数
17.2 微积分的第一基本定理
17.3 微积分的第二基本定理
17.4 不定积分
17.5 怎样解决问题：微积分的第一基本定理
17.5.1 变形1：变量是积分下限
17.5.2 变形2：积分上限是一个函数
17.5.3 变形3：积分上下限都为函数
17.5.4 变形4：极限伪装成导数
17.6 怎样解决问题：微积分的第二基本定理
17.6.1 计算不定积分
17.6.2 计算定积分
17.6.3 面积和绝对值
17.7 技术要点
17.8 微积分第一基本定理的证明
第18 章积分的方法I
18.1 换元法
18.1.1 换元法和定积分
18.1.2 如何换元
18.1.3 换元法的理论解释
18.2 分部积分法
18.3 部分分式
18.3.1 部分分式的代数运算
18.3.2 对每一部分积分
18.3.3 方法和一个完整的例子
第19 章积分的方法II
19.1 应用三角恒等式的积分
19.2 关于三角函数的幂的积分
19.2.1 sin或cos的幂
19.2.2 tan的幂
19.2.3 sec的幂
19.2.4 cot的幂
19.2.5 csc的幂
19.2.6 约化公式
19.3 关于三角换元法的积分
19.3.1 类型1：pa2？x2
19.3.2 类型2：px2+a2
19.3.3 类型3：px2？a2
19.3.4 配方和三角换元法
19.3.5 关于三角换元法的总结
19.3.6 平方根的方法和三角换元法
19.4 积分技巧总结
第20 章反常积分：基本概念
20.1 收敛和发散
20.1.1 反常积分的一些例子
20.1.2 其他破裂点
20.2 关于无穷区间上的积分
20.3 比较判别法（理论）
20.4 极限比较判别法（理论）
20.4.1 函数互为渐近线
20.4.2 关于判别法的陈述
20.5 p判别法（理论）
20.6 绝对收敛判别法
第21 章反常积分：如何解题
21.1 如何开始
21.1.1 拆分积分
21.1.2 如何处理负函数值
21.2 积分判别法总结
21.3 常见函数在∞和—∞附近的表现
21.3.1 多项式和多项式型函数在∞和—∞附近的表现
21.3.2 三角函数在∞和—∞附近的表现
21.3.3 指数在∞和—∞附近的表现
21.3.4 对数在∞附近的表现
21.4 常见函数在0附近的表现
21.4.1 多项式和多项式型函数在0附近的表现
21.4.2 三角函数在0附近的表现
21.4.3 指数函数在0附近的表现
21.4.4 对数函数在0附近的表现
21.4.5 更一般的函数在0附近的表现
21.5 如何应对不在0或1处的瑕点
第22 章数列和级数：基本概念
22.1 数列的收敛和发散
22.1.1 数列和函数的联系
22.1.2 两个重要数列
22.2 级数的收敛与发散
22.3 第n项判别法（理论）
22.4 无穷级数和反常积分的性质
22.4.1 比较判别法（理论）
22.4.2 极限比较判别法（理论）
22.4.3 p判别法（理论）
22.4.4 绝对收敛判别法
22.5 级数的新判别法
22.5.1 比式判别法（理论）
22.5.2 根式判别法（理论）
22.5.3 积分判别法（理论）
22.5.4 交错级数判别法（理论）
第23 章求解级数问题
23.1 求几何级数的值
23.2 应用第n项判别法
23.3 应用比式判别法
23.4 应用根式判别法
23.5 应用积分判别法
23.6 应用比较判别法、极限比较判别法和p判别法
23.7 应对含负项的级数
第24 章泰勒多项式、泰勒级数和幂级数导论
24.1 近似值和泰勒多项式
24.1.1 重访线性化
24.1.2 二次近似
24.1.3 高阶近似
24.1.4 泰勒定理
24.2 幂级数和泰勒级数
24.2.1 一般幂级数
24.2.2 泰勒级数和麦克劳林级数
24.2.3 泰勒级数的收敛性
24.3 一个有用的极限
第25 章求解估算问题
25.1 泰勒多项式与泰勒级数总结
25.2 求泰勒多项式与泰勒级数
25.3 用误差项估算问题
25.3.1 第一个例子
25.3.2 第二个例子
25.3.3 第三个例子
25.3.4 第四个例子
25.3.5 第五个例子
25.3.6 误差项估算的一般方法
25.4 误差估算的另一种方法
第26 章泰勒级数和幂级数：如何解题
26.1 幂级数的收敛性
26.1.1 收敛半径
26.1.2 求收敛半径和收敛区域
26.2 合成新的泰勒级数
26.2.1 代换和泰勒级数
26.2.2 泰勒级数求导
26.2.3 泰勒级数求积分
26.2.4 泰勒级数相加和相减
26.2.5 泰勒级数相乘
26.2.6 泰勒级数相除
26.3 利用幂级数和泰勒级数求导
26.4 利用麦克劳林级数求极限
第27 章参数方程和极坐标
27.1 参数方程
27.2 极坐标
27.2.1 极坐标与笛卡儿坐标互换
27.2.2 极坐标系中画曲线
27.2.3 求极坐标曲线的切线
27.2.4 求极坐标曲线围成的面积
第28 章复数
28.1 基础
28.2 复平面
28.3 复数的高次幂
28.4 解zn=w
28.5 解ez=w
28.6 一些三角级数
28.7 欧拉恒等式和幂级数
第29 章体积、弧长和表面积
29.1 旋转体的体积
29.1.1 圆盘法
29.1.2 壳法
29.1.3 总结和变式
29.1.4 变式1：区域在曲线和y轴之间
29.1.5 变式2：两曲线间的区域
29.1.6 变式3：绕平行于坐标轴的轴旋转
29.2 一般立体体积
29.3 弧长
29.4 旋转体的表面积
第30 章微分方程
30.1 微分方程导论
30.2 可分离变量的一阶微分方程
30.3 一阶线性方程
30.4 常系数微分方程
30.4.1 解一阶齐次方程
30.4.2 解二阶齐次方程
30.4.3 为什么特征二次方程适用
30.4.4 非齐次方程和特解
30.4.5 求特解
30.4.6 求特解的例子
30.4.7 解决yP和yH间的冲突
30.4.8 IVP
30.5 微分方程建模
附录A 极限及其证明
A.1 极限的正式定义
A.2 由原极限产生新极限
A.3 极限的其他情形
A.4 连续与极限
A.5 再谈指数函数和对数函数
A.6 微分与极限
A.7 泰勒近似定理的证明
附录B 估算积分
B.1 使用条纹估算积分
B.2 梯形法则
B.3 辛普森法则
B.4 近似的误差
符号列表
索引

2.2　扩展三角函数定义域

上表 (你背熟了吗？) 仅仅包括介于 0 到 π/2 的一些角. 但事实上, 我们可以取任意角的正弦或者余弦, 哪怕这个角是负的. 对于正切函数, 我们则不得不小心些. 例如, 上面我们看到的 tan (π/2) 是无定义的. 尽管如此, 我们还是能够对几乎每一个角取正切.

让我们首先来看看介于 0 到 2π (记住, 2π 就是 360°) 的角吧. 假设你想要计算 sin (θ) (或 cos (θ) 或 tan (θ)), 其中 θ 是介于 0 到 π/2 的角. 为了看得更清楚, 我们先来画一个带有一点古怪标记的坐标平面, 如图 2-5 所示.

图　2-5

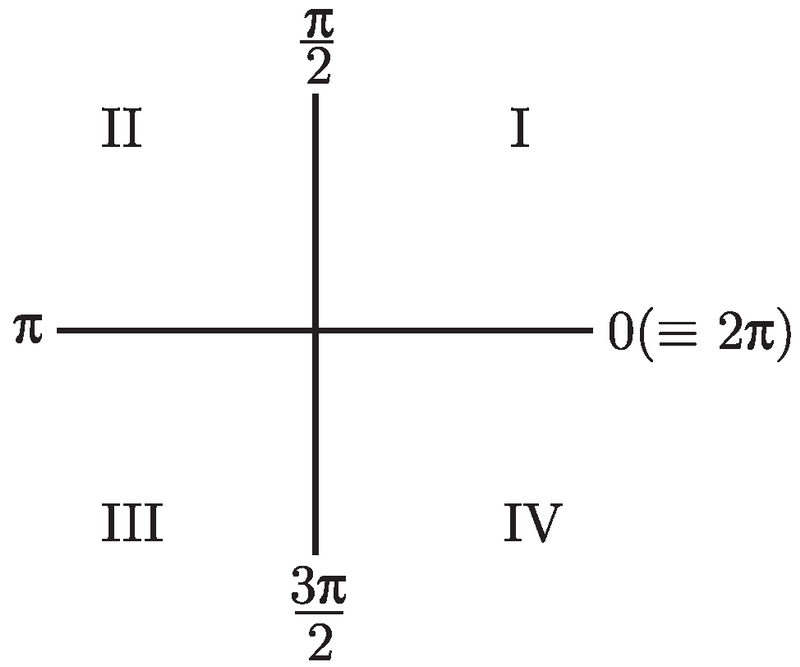
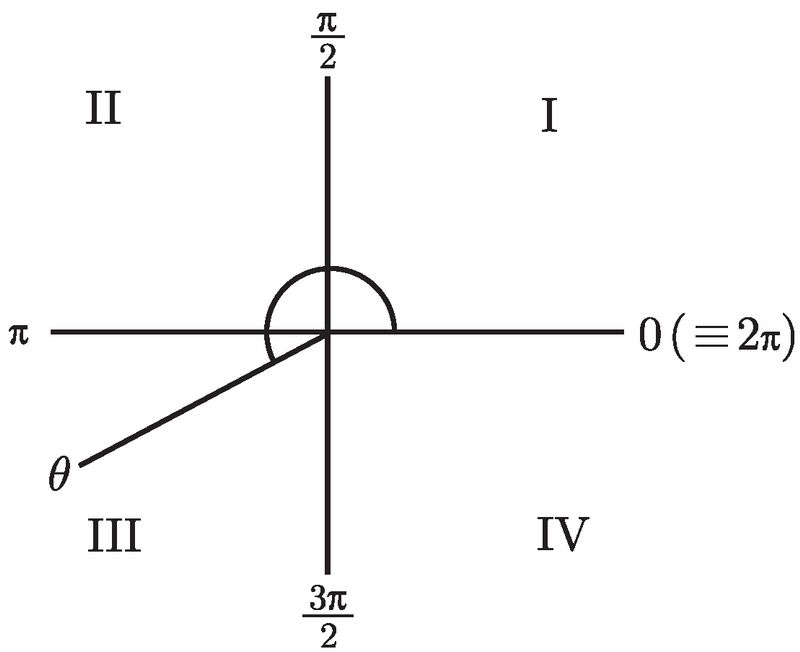
注意到坐标轴将平面分成了四个象限, 标记为Ⅰ到Ⅳ, 且标记的走向为逆时针方向. 这些象限分别被称为第一象限、第二象限、第三象限和第四象限. 下一步是要画一条始于原点的射线 (就是半直线). 那么究竟是哪一条射线呢？这取决于角 θ. 来想象一下, 你自己站在原点上, 面向 x 轴的正半轴. 现在沿着逆时针方向转动角 θ, 然后你沿着一条直线向前走. 你的足迹就是你要找的那条射线了.

现在, 图 2-5 (以及图 2-2) 中的其他标记就说得通了. 事实上, 如果你转动了角 π/2, 你将正面向上并且你的足迹将是 y 轴的正半轴. 如果你转动了角 π, 你将得到 x 轴的负半轴. 如果你转动了角 3π/2, 你将得到 y 轴的负半轴. 最后, 如果你转动了角 2π, 那么就又会回到了你起始的那个位置, 即面向 x 轴的正半轴. 这就好像你根本没转动过! 这就是为什么图中会有 0 ≡ 2π. 对于角度而言, 0 和 2π 是等价的.

好了, 让我们取某个角 θ 并以恰当的方式画出它. 或许它就在第三象限的某个地方, 如图 2-6 所示.

图　2-6

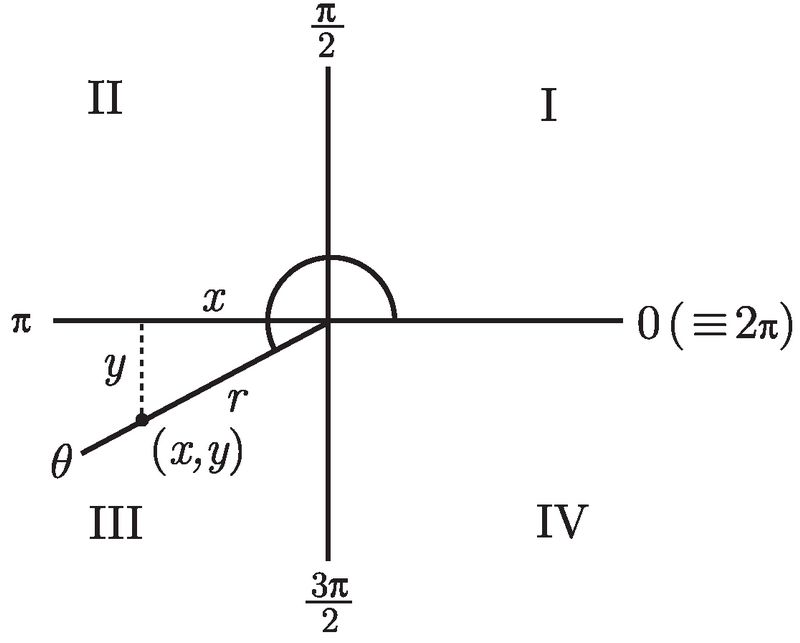
注意到我们将这条射线标记为 θ, 而不是这个角本身. 不管怎样, 现在在这条射线上选取某个点并从该点画一条垂线至 x 轴. 我们对三个量感兴趣：该点的 x 坐标和 y 坐标 (当然它们被称为 x 和 y), 以及该点到原点的距离, 我们称为 r. 注意, x 和 y 可能会同时为负 (事实上, 在图 2-7 中它们均为负). 然而, r 总是正的, 因为它是距离. 事实上, 根据毕达哥拉斯定理 (即勾股定理), 不管 x 和 y 是正还是负, 我们总会有 . (平方会消除任何负号.)

图　2-7

有了这三个量, 我们就可以定义如下的三个三角函数了：

　将量 x、y 和 r 分别解释为邻边、对边和斜边, 这些函数恰好就是 2.1 节中的固定公式了. 不过等一下, 如果你在那条射线上选取了另外一个点, 那会是什么样子呢？这不要紧, 因为你得到的新的三角形和原来的那个三角形是相似的, 而上述比值不会受到任何影响. 事实上, 为方便起见, 我们常常假设 r = 1, 这样得到的点 (x, y) 会落在所谓的单位圆 (就是以原点为中心, 半径为 1 的圆) 上.

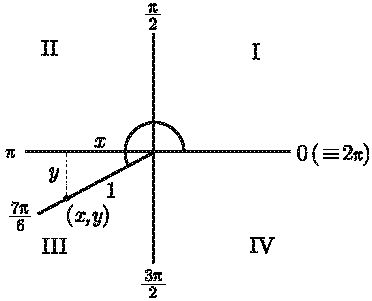
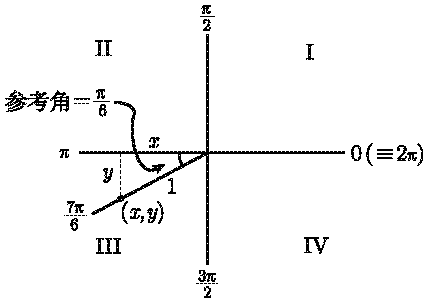
现在来看一个例子. 假设, 我们想求 sin (7π/6). 首先, 7π/6 会在第几象限呢？我们需要决定 7π/6 会出现在列表 0, π/2, π, 3π/2, 2π 的哪个地方. 事实上, 7/6 大于 1 但小于 3/2, 故 7π/6 在 π 和 3π/2 之间. 事实上, 图 2-8 看起来很像前面的例子.

图　2-8

因此, 角 7π/6 在第三象限. 然后, 我们选取了该射线上的一点, 该点至原点的距离 r = 1, 并从该点至 x 轴做了一条垂线. 由前述公式可知, sin (θ) = y/r = y (因为 r = 1), 因此, 我们还是要求出 y. 好吧, 那个小角, 就是在 7π/6 处的射线和 x 轴的负半轴 (其为 π) 之间的角一定是这两个角的差, 即 π/6. 这个小角被称为参考角. 一般来说, θ 的参考角是在表示角 θ 的射线和 x 轴之间的最小的角, 它必定介于 0 到 π/2. 在我们的例子中, 到 x 轴的最短路径是向上, 所以参考角如图 2-9 所示. 因此, 在那个小三角形中, 我们知道 r= 1, 以及角为 π/6. 似乎答案就是 y = sin (π/6) = 1/2, 但这是错的! 由于在 x 轴的下方, y 一定为负值. 也就是说, y = -1/2. 因为 sin (θ) = y, 我们也就证明了 sin (7π/6) = -1/2. 对于余弦来说, 也可以重复这个过程, 求出 . 毕竟, 由于点 (x, y) 在 y 轴的左侧, 因此 x 必须为负. 这样就证明了 , 并且识别出点 (x, y) 即为点 .

图　2-9

2.2.1　ASTC 方法

上例中的关键是将 sin (7π/6) 和 sin (π/6) 联系起来, 其中 π/6 是 7π/6 的参考角. 事实上, 并不难看出任意角的正弦就是其参考角正弦的正值或负值! 这就使问题缩小到两种可能性上, 而且没有必要再 x, y 或 r 如此这般麻烦. 因此, 在我们的例子中, 只需要求出 7π/6 的参考角, 即 π/6; 这就会立即可知 sin (7π/6) 等于 sin (π/6) 或 -sin (π/6), 而我们只需从中选出正确的结果. 我们发现, 结果是负的那个, 因为 y 是负的.

事实上, 在第三或第四象限中的任意角的正弦必定为负, 因为那里的 y 为负. 类似地, 在第二或第三象限中的任意角的余弦必定为负, 因为那里的 x 为负. 正切是比值 y/x, 它在第二和第四象限为负 (由于 x 和 y 中的一个为负, 但不全为负), 而在第一和第三象限为正.

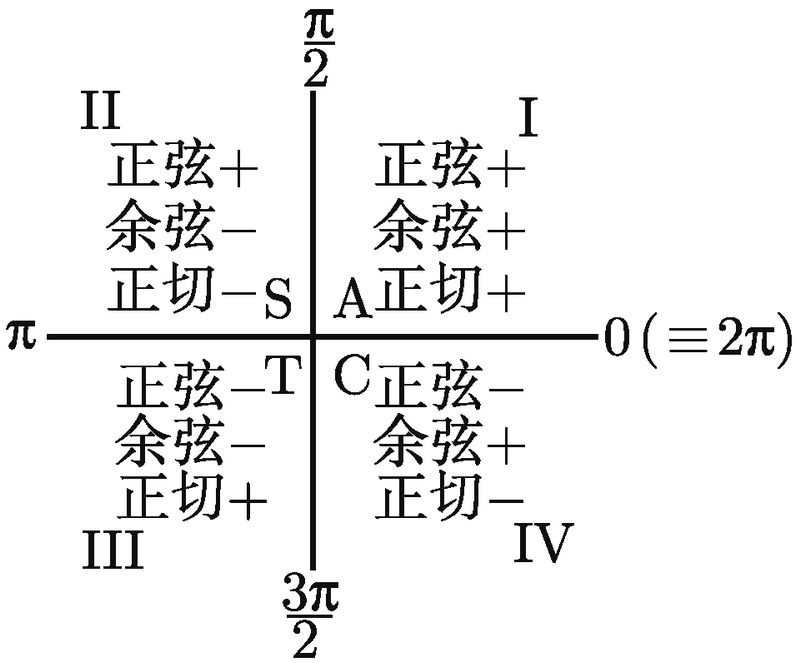
让我们来总结一下这些发现吧. 首先, 所有三个函数在第一象限 (I) 中均为正. 在第二象限 (II) 中, 只有正弦为正, 其他两个函数均为负. 在第三象限 (III) 中, 只有正切为正, 其他两个函数均为负. 最后, 在第四象限 (IV) 中, 只有余弦为正, 其他两个函数均为负. 具体如图 2-10 所示.

图　2-10

事实上, 你只需要记住图表中的字母 ASTC 就行了. 它们会告诉你在那个象限中哪个函数为正. “A” 代表 “全部”, 意味着所有的函数在第一象限均为正. 显然, 其余的字母分别代表正弦、正切和余弦. 在我们的例子中, 7π/6 在第三象限, 所以只有正切函数在那里为正. 特别地, 正弦函数为负, 又由于我们已经把 sin (7π/6) 的可能取值缩小到 1/2 或 -1/2 了, 因此结果一定是负的那个, 即 sin (7π/6) = -1/2.

ASTC 图唯一的问题在于, 它没有告诉我们该如何处理角 0, π/2, π 或 3π/2, 因为它们都位于坐标轴上. 这种情况下, 最好是先忘记所有 ASTC 的内容, 然后以恰当的方式画一个 y = sin (x) (或 cos (x), 或 tan (x)) 的图像, 并且从图像中读取数值. 我们将在 2.3 节对此进行研究.

以下是用 ASTC 方法来求介于 0 到 2π 的角的三角函数值的总结.

(1) 画出象限图, 确定在该图中你感兴趣的角在哪里, 然后在图中标出该角.

(2) 如果你想要的角在 x 轴或 y 轴上 (即没有在任何象限中), 那么就画出三角函数的图像, 从图像中读取数值 (2.3 节有一些例子).

(3) 否则, 找出在代表我们想要的那个角的射线和 x 轴之间最小的角, 这个角被称为参考角.

(4) 如果可以, 使用那张重要的表来求出参考角的三角函数值. 那就是你需要的答案, 除了你可能还需要在得到的值前面添一个负号.

(5) 使用 ASTC 图来决定你是否需要添一个负号.

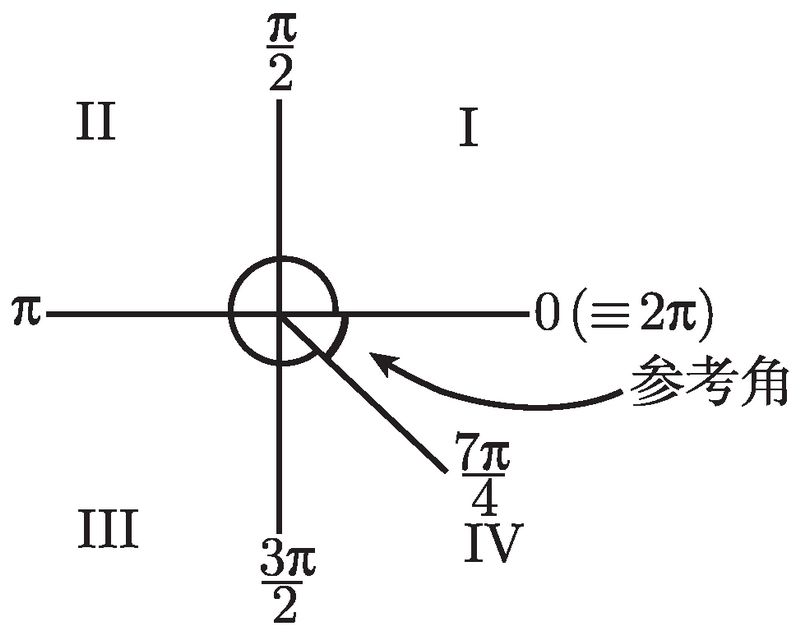
来看一些例子. 如何求 cos (7π/4) 和 tan (9π/13) 呢？我们一个一个地看. 对于 cos (7π/4), 我们注意到 7/4 介于 3/2 和 2 之间, 故该角必在第四象限, 如图 2-11 所示.

图　2-11

为了求出参考角, 注意到我们必须向上走到 2π (注意! 不是到 0), 因此, 参考角就是 2π 和 7π/4 的差, 即 (2π - 7π/4), 或简化为 π/4. 所以 cos (7π/4) 是正的或负的 cos (π/4). 根据表, cos (π/4) 是 . 但到底是正的还是负的呢？由 ASTC 图可知, 在第四象限中余弦为正, 故结果为正的那个：.

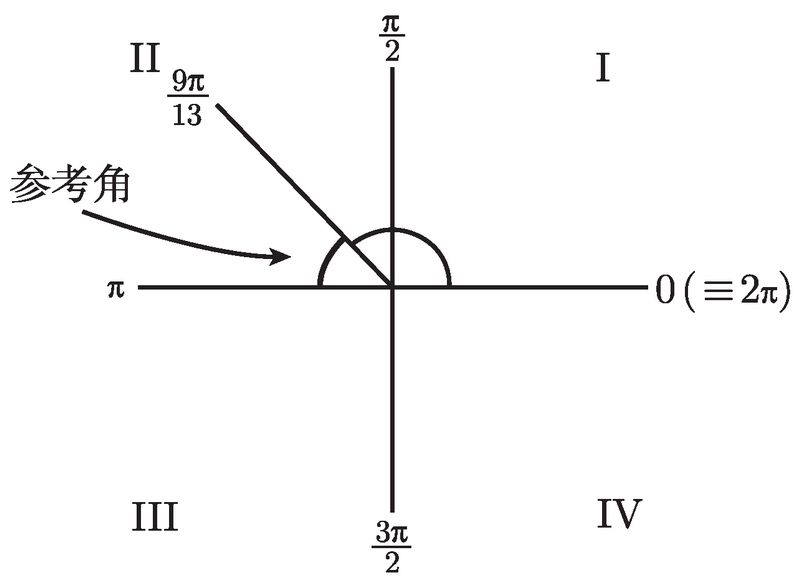
　现在来看一下 tan (9π/13). 我们发现 9/13 介于 1/2 和 1 之间, 故角 9π/13 在第二象限, 如图 2-12 所示.

图　2-12

这一次, 我们需要走到 π 以到达 x 轴, 故参考角就是 π 和 9π/13 的差, 即 (π-9π/13), 或简化为 4π/13. 这样, 我们知道 tan (9π/13) 是正的或负的 tan (4π/13). 哎呀, 可是数 4π/13 没有在我们的表里面, 因此不能化简 tan (4π/13). 可我们还是需要确定它是正的还是负的. 那好, ASTC 图显示, 在第二象限中只有正弦为正, 故正切一定为负, 于是 tan (9π/13) = -tan (4π/13). 这就是不使用近似可以得到的最简形式. 在求解微积分问题的时候, 我不建议取近似结果, 除非题目中有明确要求. 一个常见的误解是, 当你计算如同 -tan (4π/13) 这样的问题时, 由计算器计算出来的数就是正确答案. 其实, 那只是一个近似! 所以你不应该写

因为它不正确. 就应该写 -tan (4π/13), 除非有特别的要求, 让做近似. 在那种情况下, 使用约等号和更少的小数位数, 并恰当化整近似 (除非要求保留更多小数位数)：

顺便说一下, 你应该少用计算器. 事实上, 一些大学甚至不允许在考试中使用计算器! 因此, 你应该尽量避免使用计算器.

2.2.2　[0, 2π] 以外的三角函数

还有一个问题, 就是如何取大于 2π 或小于 0 的角的三角函数. 事实上, 这并不太难, 简单地加上或减去 2π 的倍数, 直到你得到的角在 0 和 2π 之间. 你看, 它并不是在 2π 就完了. 它是一直在旋转. 例如, 如果我让你站在一点面向正东, 然后逆时针方向旋转 450°, 一种自然的做法是, 你旋转一整周, 然后再旋转 90°. 现在你应该是面向正北. 当然, 另一种不那么头晕目眩的做法是, 你只逆时针方向旋转 90°, 而你面向的是同样的方向. 因此, 450° 和 90° 是等价的角. 当然, 这对于弧度来说也一样. 这种情况下, 5π/2 弧度和 π/2 弧度是等价的角. 但为什么要止步于旋转一周呢？9π/2 弧度又如何？这和旋转 2π 两次 (这样我们得到 4π), 然后再旋转 π/2 是一样的. 因此, 在得到最终的 π/2 之前, 我们做了两周徒劳的旋转. 旋转周数无关紧要, 我们再次得到 9π/2 和 π/2 等价. 这个过程可以被无限地扩展下去, 以得到等价于 π/2 的角的一个家族：

当然, 这其中的每一个角都比第一个角多一个整周旋转, 即 2π. 但这仍然还没算完. 如果你做了所有这些逆时针旋转, 并感到头晕目眩, 或许你也会要求做一个或两个顺时针旋转来缓和一下. 这就相当于一个负角. 特别地, 如果你面向东, 我让你逆时针旋转 -270°, 对我这个怪异要求唯一合理的解释就是顺时针旋转 270°(或 3π/2). 显然, 你最终仍然会面向正北, 因此, -270° 和 90° 一定是等价的. 确实, 我们将 360° 加到 -270° 上就会得到 90° . 使用弧度, 我们则看到, -3π/2 和 π/2 是等价的角. 另外, 我们可以要求更多负的 (顺时针方向) 整周旋转. 最后, 以下就是等价于 π/2 的角的完全的集合：

这个序列没有开端也没有结束. 当我说它是 “完全的” 时, 我用前后两头的省略号代表了无穷多个角. 为了避免这些省略号, 我们可以使用集合符号 {π/2 + 2πn}, 其中 n 可以取所有整数.

　来看一下是否可以应用它吧. 如何求 sec (15π/4) 呢？首先, 注意到如果我们能够求出 cos (15π/4), 所要做的就是取其倒数以得到 sec (15π/4). 因此, 让我们先求 cos (15π/4). 由于 15/4 大于 2, 让我们先试着消去 2. 这样, 15/4 - 2 = 7/4, 现在它介于 0 和 2 之间, 这看上去很有希望了. 代入 π, 我们看到 cos (15π/4) 和 cos (7π/4) 是一样的, 并且我们已经求出其结果为 . 因此, . 取其倒数, 我们发现 sec (15π/4) 就是 .

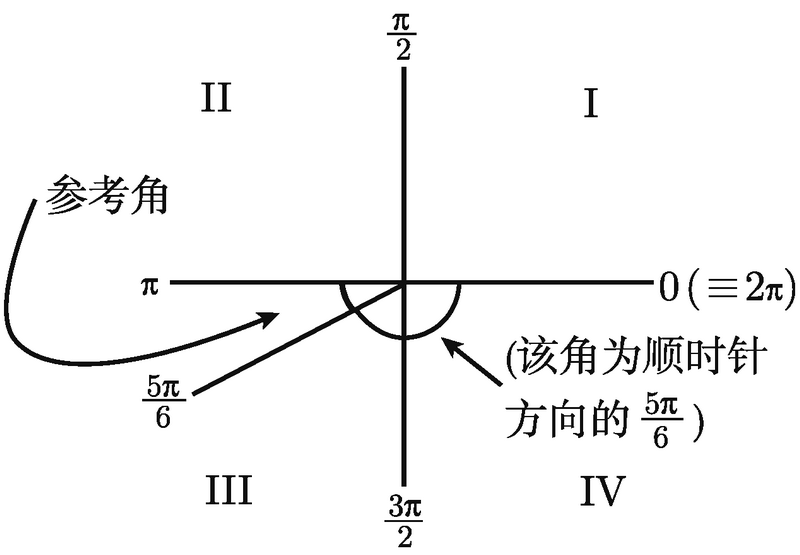
　最后, sin (-5π/6) 又如何呢？有很多方法来求解此问题, 但上面提到的方法是试着将 2π 的倍数加到 -5π/6 上, 直到结果是介于 0 到 2π 的. 事实上, 2π 加上 -5π/6 得 7π/6, 因此, sin (-5π/6) = sin (7π/6), 后者我们已经知道等于 -1/2. 另外, 我们也可以直接画图 2-13.