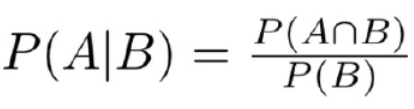概率论之概念解析：引言篇

2018 年 1 月 8 日 专知专知内容组（编）

【导读】专知这两天推出概率论之概念解析系列：极大似然估计和贝叶斯推断进行参数估计，大家反响热烈，数据科学家Jonny Brooks-Bartlett的系列博客深入浅出地给大家讲解了极大似然估计和贝叶斯推断的原理，把枯燥的数学公式用简单的例子给大家解释清楚，今天专知推出其系列博客引言部分——概率论之概念解析：引言。这篇主要是介绍概率一些基本的定义以及概率论的一些概念，博文内容涉及到什么是随机变量，边缘概率、联合概率和条件概率的关系。这是一篇非常不错的概率基本概念入门文章，希望对大家有所帮助。

概率论基础概念系列博客——概率论之概念解析：极大似然估计和贝叶斯推断进行参数估计，阅读专知以前推出的报道：

概率论之概念解析：极大似然估计

概率论之概念解析：用贝叶斯推断进行参数估计

Probability concepts explained: Introduction

【导读】近年来，我读过许多关于概率论不同方面的文献和论文，而且每一篇文章似乎都需要不同层次的前提知识来理解它们。我绝对不是这个领域的专家，但是我觉得我可以写成一系列的文章，用来解释概率论的各种概念。这是本系列的第一篇，将介绍一些基本的定义。

▌定义和符号

概率通常与至少一个事件有关。这个事件可以是任何事情。一个小例子比如掷骰子或从袋子里抽出一个彩色的球。在这些例子中，事件的结果是随机的（你不能确定骰子在滚动时显示的值），所以表示这些事件结果的变量被称为随机变量（random variable，通常缩写为RV）。

我们通常感兴趣的是知道一个随机变量取某一个值的概率。例如，当我掷出一个每一个面都等价的六面骰时，掷到3的概率是多少？“公平（fair）”这个词在这里很重要，因为它告诉我们骰子最后落在六个面（1，2，3，4，5和6）的任何一个面上的可能性是相等的。现在从直觉上看，你可能会告诉我答案是1/6。这是正确的！但是，我们怎么用数学方法来写呢？首先，我们需要知道，这里的随机变量是与掷骰子有关的事件的结果。通常情况下，随机变量用大写字母表示，这里我们用X来表示它。因此，我们想知道X = 3的概率是多少。但是由于数学家在写东西时很懒惰，问“概率是多少？”他们是用字母P表示的。因此，我们可以用“P（X = 3）”这个数学术语来写“当我投掷一个公平的六面骰子，落在3上的概率是多少？ ”

▌三种类型的概率

上面介绍了随机变量的概念和概率的一些符号。但是，概率可能会相当复杂。也许首先要了解的是有多少种不同类型的概率。它可以是边缘，联合或有条件的。

边缘概率（Marginal Probability）：如果A是一个事件，那么边缘概率就是事件发生的概率P（A）。例如：假设我们有一副传统扑克牌，一个边缘概率的例子就是从一副牌中抽取的一张牌是红色的概率，即：P（红色）= 0.5。

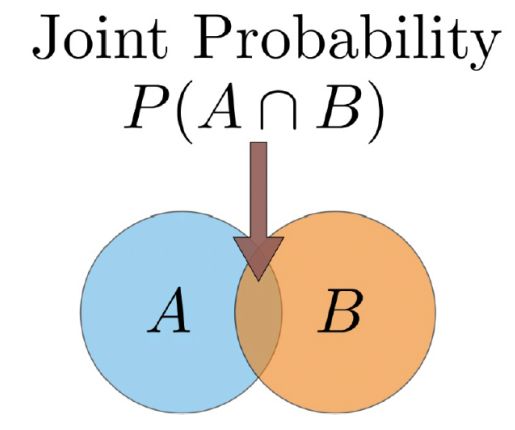
联合概率（Joint Probability）：两个或多个事件相交（交集）的概率。在视觉上，它是维恩图（Venn Diagram）上两个事件的圆的交集（见下图）。如果A和B是两个事件，那么这两个事件的联合概率被写为P（A∩B）。例如：从一副牌中抽取的卡片是红色并且值为4的概率是P（红色和4）= 2/52 = 1/26。（一副传统扑克牌中有52张牌，红色的是红心和方片，所以是2张）。稍后我们会更详细地讨论这个例子。

条件概率（Conditional Probability）：条件概率是在其他事件发生时某事件发生的概率。如果A和B是两个事件，那么先发生了B才发生A的条件概率被写为P（A|B）。例如：在已知我们抽的牌是红色的情况下，一张牌是4的概率是P（4|red）= 2/26 = 1/13。（一副牌里有52张牌，26个是红色的，26个是黑色的，现在因为我们已经选了一张红牌，所以我们知道只有26张牌可以选择，所以这就是为什么第一个分母是26）。

图：维恩图显示了2个事件A和B的结果的“空间”。在该图中，2个事件重叠。这个重叠表示联合概率，即事件A和事件B共同发生的概率。如果事件之间没有重叠，则联合概率将为零。

▌连接三种类型的概率：一般乘法法则

一般乘法法则是一个很漂亮的等式，它把所有3种概率联系起来:

▌进一步解释这些例子

有时区分联合概率和条件概率可能是相当混乱的，所以用一副扑克牌挑一张牌的例子，我们可以尝试克服这个差异。

在这个例子中，我们想要找到一张红色4的卡牌的概率，即联合概率为P（红色和4），我想让你想象一个场景，所有52张牌面朝下，随机选取一张。在这52张牌中，只有2张是既是红色的又是牌面为4的牌。所以联合概率是2/52 = 1/26

如果我们已经知道卡牌是红色，我们想要找到牌面是4的卡牌的概率是多少，即条件概率P（4 |红色），那么我想让你再想象一下，共有52张牌。但是，在随机挑选一张牌之前，你先整理卡牌，然后选择26个红色的卡牌。现在你把这26张牌面朝下，随机挑一张牌。再次，这些红牌中的有2张牌面为4，所以条件概率是2/26 = 1/13。

另外，如果你喜欢数学，我们可以使用我们上面定义的一般乘法规则来计算联合概率。我们首先重新排列，使联合概率P（A∩B）成为等式的主题（换言之，让P（A∩B）置于等号的左边，并把所有其他的东西放在右边）。重新排列后得到P（A∩B）= P（A|B）✕ P（B）。设A为卡片为4的事件，B为卡片为红色的事件。如上所述，P（A | B）= 1/13，P（B）= 1/2（半数牌是红色）。因此P（A∩B）= 1/13✕1/2 = 1/26。

▌概率规则：“和”，“或”

“和”（“and”）规则

我们已经看到“和”场景被伪装成联合概率，但是我们还不知道如何计算“和”场景中的概率。我们来看一个例子。假设我们有两个事件：事件A - 抛一枚均匀的硬币，事件B - 掷一个均匀的骰子。我们可能想知道的是掷出6和硬币落地正面朝上的可能性。因此，为了计算掷出6和硬币正面朝上的联合概率，我们可以重新排列上面的一般乘法规则，得到P（A∩B）= P（A|B）✕ P（B）。我们知道事件A是抛硬币，B是掷骰子。所以P（A|B）这个术语在问“当我掷骰子掷出6的时候，抛硬币正面朝上的概率是多少”？我们凭直觉就知道抛硬币的结果并不取决于掷骰子的结果。这些事件是独立的。在这种情况下，无论我们骰子掷出来的是什么，抛硬币的结果将是相同的。在数学上，我们表示为P（A|B）= P（A）。因此，当事件是独立的时候，联合概率就是每个独立事件边缘概率的乘积：P（A∩B）= P（A）✕ P（B）。所以P（硬币正面朝上和骰子掷出6）= P（A = 正面，B = 6）= 1/2×1/6 = 1/12。

请注意，我写成了P（A = 正面，B = 6）。事件之间的逗号是联合概率的简写（在很多文献中你会看到这种写法）。

应该指出的是，在现实世界的许多场景中，事件被假定为独立的（即使事实并非如此）。这主要是因为这样做使数学变得容易得多。好处是，结果往往非常有用。朴素贝叶斯方法可能是数据科学中最常见的一个例子，通常在文本分类问题上给出相当好的结果。

“或”（“or”）规则

用"和"的规则，我们必须将个体概率相乘。当我们处于“或”情境中时，我们必须用个体概率之和减去它们的交集。在数学上，我们把它写成P（A∪B）= P（A）+ P（B）- P（A∩B）。我们为什么要这样做？让我们回到上图中的维恩图。如果我们把A的圆和B的圆加起来，那么意味着我们把它们的交集添加了两次。所以我们需要减去交集。

让我们来改变一下上面的例子，来找出骰子掷出6或者硬币落地正面朝上的概率。这时，P（硬币正面朝上或掷出6）= P（A = 正面 ∪ B = 6）= 1/2 + 1/6 - 1/12 = 6/12 + 2/12 - 1/12 = 7/12

请注意，∪符号被称为“联合”，并在“或”场景中使用。

有时我们不需要减去交集。当维恩图中的两个圆圈不重叠时就不需要减。当两个事件的圆不重叠时，我们说这些事件是相互排斥的。这意味着交集为零，在数学上写为P（A∩B）= 0。我们来举一个列子说明这种情况。假设我们掷骰子，我们想知道掷出5或者掷出6的概率。这两个事件是相互排斥的，因为我不能同时掷出5和6。因此，它们在维恩图中的圆圈不重叠。所以掷出5或6的概率等于1/6 + 1/6 = 2/6 = 1/3（我们没有减去任何东西）。

▌结束语

感谢您看到这里。我希望我这种漫无目的的讲授方式能被您接受如果有什么不清楚的地方，或者我在上面犯了一些错误，请随时留言发表评论。在本系列的接下来的文章中，我将介绍一些更高级的概念。下一篇文章将解释最大的可能性，并通过一个例子来讲述。

谢谢阅读！

原文链接：

https://towardsdatascience.com/probability-concepts-explained-introduction-a7c0316de465

Jonny Brooks-Bartlett是知名的数据科学家、演说家；数学家，主页：

https://towardsdatascience.com/@jonnybrooks04?source=post_header_lockup

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

同时欢迎各位用户进行专知投稿，详情请点击：

【诚邀】专知诚挚邀请各位专业者加入AI创作者计划！了解使用专知！