重新思考图卷积网络：GNN只是一种滤波器

会员服务 ·

重新思考图卷积网络：GNN只是一种滤波器

2019 年 6 月 3 日 新智元

新智元报道

来源：arxiv

编辑：肖琴

【新智元导读】最新研究提出，图神经网络仅对特征向量进行低通滤波，不具有非线性流形学习特性。论文提出了一种基于图形信号处理的理论框架，用于分析图神经网络。

图神经网络已成为解决图结构数据机器学习问题的最重要技术之一。

最近关于顶点分类(vertex classification)的工作提出了深度和分布式的学习模型，以实现高性能和可扩展性。

但最近，一篇题为“Revisiting Graph Neural Networks: All We Have is Low-Pass Filters”的论文引起关注，文中提出，图神经网络仅仅是对特征向量进行低通滤波而已。

来自东京工业大学、RIKEN的两位研究人员发现，基准数据集的特征向量对于分类任务来说已经能提供很多有用信息，而图结构仅仅提供了一种对数据进行去燥的方法。

论文提出了一种基于图形信号处理的理论框架，用于分析图神经网络。

作者称，他们的结果表明，图神经网络仅对特征向量进行低通滤波(low-pass filtering)，不具有非线性流形学习特性。论文进一步研究了它们对特征噪声的适应力，并对基于GCN的图神经网络设计提出了一些见解。

什么时候应该使用图神经网络？

图神经网络(Graph neural networks, GNN)是一类能够从图结构数据中学习的神经网络。近年来，用于顶点分类和图形同构测试的图神经网络在多个基准数据集上取得了良好的效果，并不断开创新的最先进技术性能。随着ChebNet和GCN在顶点分类方面获得成功，许多GNN变体被提出来解决社交网络、生物学、化学、自然语言处理、计算机视觉和弱监督学习方面的问题。

在半监督顶点分类问题中，我们观察到，图卷积层(GCN)的参数只会导致过拟合。类似的观察在简单的架构(如SGC)和更复杂的脚骨(如DGI)中都曾被报告。

基于这种现象，Felix Wu等人提出将图神经网络简单地看作是特征传播(feature propagation)，并提出了一种在许多基准数据集上具有最先进性能的高效模型。Kawamoto等人对图分区设置下未经训练的GCN-like GNNs进行了相关理论评述。

从这些先前的研究中，一个很自然的问题出现了：为什么、以及何时图神经网络在顶点分类任务中表现很好？

换句话说，是否存在一个顶点特征向量的条件，使得图神经网络模型即使没有经过训练也能很好地工作？

那么，我们能否找到基准图神经网络(如SGC或GCN)失败的实际反例?

在本研究中，我们从图信号处理的角度来回答上述问题。在形式上，我们考虑了一个图的半监督学习问题。

给定一个图G = (V, E)，每个顶点i∈V都有一个特征x(i)∈x，和标记y(i)∈y，其中x是d维欧氏空间R d, Y = R用于回归， Y ={1，…， c}用于分类。任务是从特征x(i)中学习预测标签y(i)的假设。

然后，我们描述了这个问题的图神经网络解决方案，并对最常用的基准模型GCN及其简化的变体SGC的机制提供了见解。

本研究三大贡献

图信号处理(Graph signal processing, GSP)将顶点上的数据视为信号，应用信号处理技术来理解信号的特征。通过组合信号(特征向量)和图结构(邻接矩阵或邻接矩阵的变换)，GSP启发了图结构数据学习算法的发展。在标准信号处理问题中，通常假设观测值包含一些噪声，并且底层的“真实信号”具有低频。这里，我们对我们的问题提出了类似的假设。

假设1：输入特征包括低频真实特征和噪声。真实特征为机器学习任务提供了足够的信息。

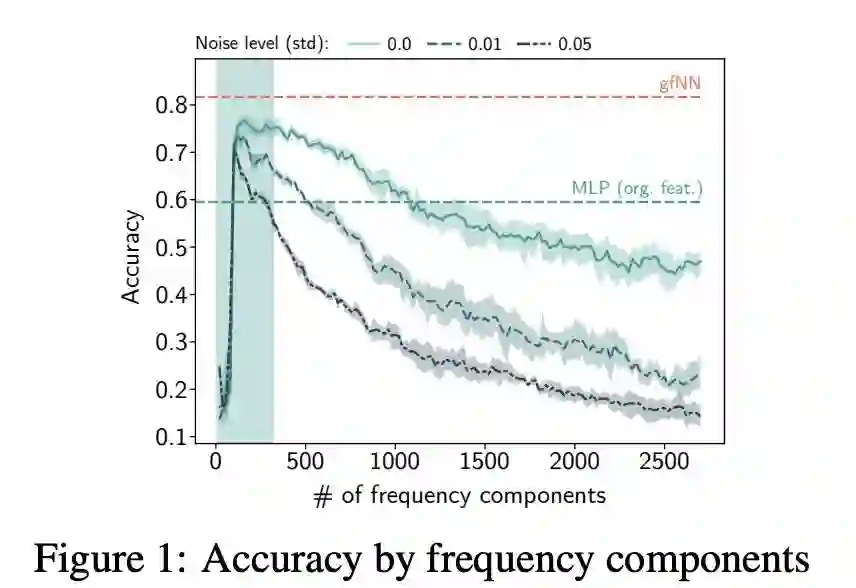
本研究的第一个贡献是验证了常用数据集的假设1(第3节)。图1显示了针对不同频率成分(frequency components)的特征训练的2层感知器(MLPs)的性能。在所有基准数据集中，我们看到只有少数频率成分有助于学习。在特征向量中加入更多的频率成分只会导致性能下降。反过来，当我们将高斯噪声N (0, σ2 ) 添加到特征中时，分类精度变得更糟了。

图1：频率成分的精度

最近的许多GNN都是建立在图信号处理的基础上的。最常见的做法是用(增强)规范化邻接矩阵I − L˜ 和矩阵X的特性。在图信号处理的文献中，这种操作在图上过滤信号(filters signals)，而不显式地对标准化拉普拉斯矩阵进行特征分解。在这里，我们将这个增强的标准化邻接矩阵及其变体称为可互换的图滤波器(graph filters)和传播矩阵(propagation matrices)。

本研究的第二个贡献表明，将图信号与传播矩阵相乘对应于低通滤波(第4节，尤其是定理3)，此外，我们还证明了观测信号与低通滤波器之间的矩阵乘积是真实信号优化问题的解析解。与最近的图神经网络设计原理相比，我们的结果表明图卷积层只是低通滤波(low-pass filtering)。因此，不需要学习图卷积层的参数。

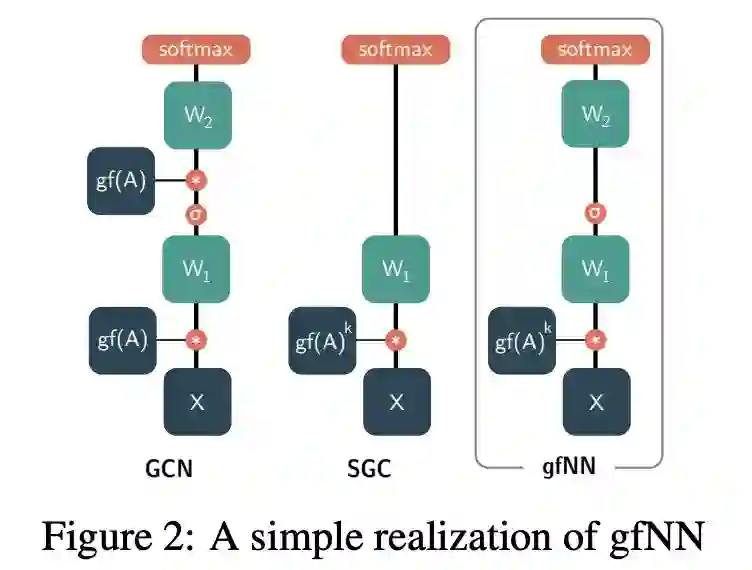
在理论理解的基础上，我们提出了一种新的基准框架，称为gfNN((graph filter neural network, 图滤波神经网络)，对顶点分类问题进行了实证分析。

gfNN由两个步骤组成：

通过与图滤波矩阵的乘法实现滤波特性;
通过机器学习模型学习顶点标签。

我们使用图2中的一个简单实现模型演示了框架的有效性。

图2：gfNN的一个简单实现

本研究的第三个贡献是以下定理：

定理2：在假设1下，SGC、GCN和gfNN的结果与使用真实特征的相应神经网络的结果相似。

定理7表明，在假设1下，gfNN和GCN具有相似的高性能。由于gfNN在学习阶段不需要邻接矩阵的乘法，因此它比GCN要快得多。此外，gfNN对噪声的容忍度也更高。

最后，我们将gfNN与SGC模型进行了比较。虽然SGC在基准数据集上计算速度快、精度高，但我们的分析表明，当特征输入是非线性可分的时，SGC会失败，因为图卷积部分对非线性流形学习没有贡献。为了实证证明这个观点，我们创建了一个人工数据集。

实验和结果

为了验证前面提出的观点，我们设计了两个实验。在实验E1中，我们将不同水平的白噪声加入到真实数据集的特征向量中，并比较不同基线模型的分类精度。

在实验E2中，我们研究了一个具有复杂的特征空间的人工数据集，以证明SGC等简单模型在分类时会失败。

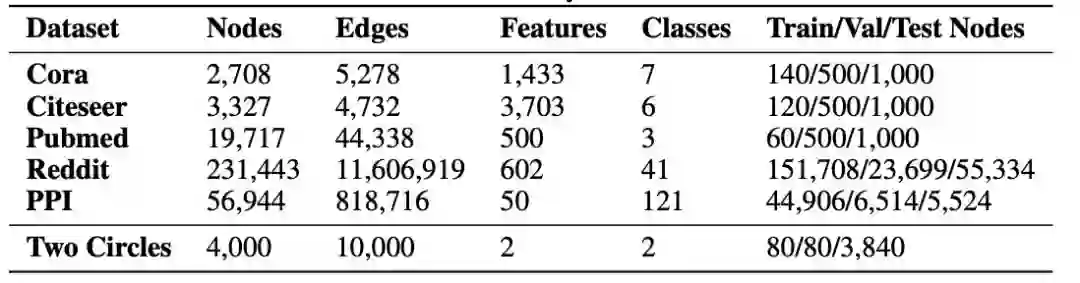
表1给出了每个数据集的概述。

表1：用于顶点分类的实际基准数据集和合成数据集

神经网络

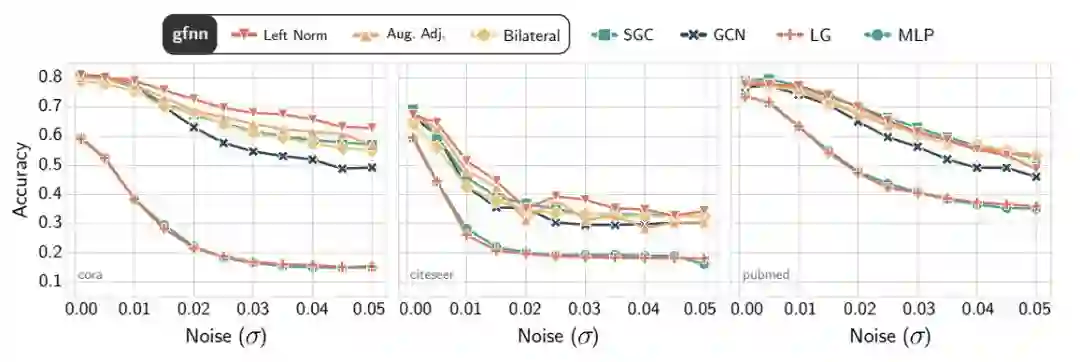
图4:Cora(左)、Citeseer(中)和Pubmed(右)数据集上的基准测试精度。噪声水平通过在特征值上增加白噪声的标准差来测量。

图像滤波器的去噪效果

对于每个数据集表1中,我们介绍一个白噪声N(0, 2)为特征向量?范围内(0.01,0.05)。根据定理8和定理7的含义，由于GCN的一阶去噪特性，它对特征噪声的容忍度较低。

随着噪声水平的增加，我们在图4中可以看到，GCN、Logistic回归(LR)和MLP更容易对噪声进行过拟合。另一方面，gfNN和SGC对噪声的容忍度差不多。

图过滤器的表现力

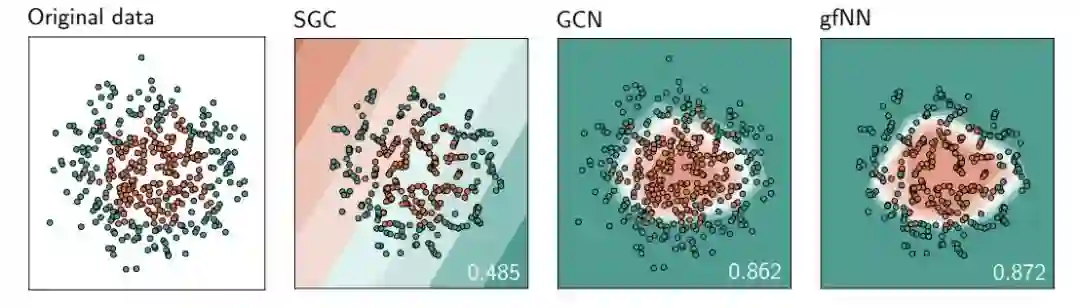
图5：基于两个圆形图案生成的500个数据样本的决策边界

表2：随机train/val/test分段的平均测试精度(5次)

总结

很少有工作涉及GCN架构的限制。Kawamoto等人采用平均场方法对一个简单的GCN模型进行了统计物理分析。他们的结论是，反向传播既不能提高基于GCN的GNN模型的准确性，也不能提高其可检测性。Li et al.在有限的标签数据设置下对多层的GCN模型进行了实证分析，指出如果标签数据太少或者叠加层太多，GCN的性能就会下降。虽然这些结果为GCN提供了很有洞察力的观点，但是它们并没有充分地回答这个问题：我们什么时候应该使用GNN?

我们的结果表明，如果假设1成立，我们应该使用GNN方法来解决给定的问题。从我们的角度来看，从GCN派生出来的GNNs只是简单地执行噪声滤波，并从去噪数据中学习。

基于我们的分析，我们提出了GCN和SGC可能无法执行的两种情况：噪声特征和非线性特征空间。然后，我们提出一个在这两种情况下都能很好地工作的简单方法。

近年来，基于GCN的神经网络在点云分析、弱监督学习等领域得到了广泛的应用。随着输入特征空间的复杂化，我们提议重新审视当前基于GCN的GNNs设计。在计算机视觉中，GCN层并不是卷积层，我们需要把它看作一种去噪机制。因此，简单地叠加GCN层只会给神经网络设计带来过拟合和复杂性。

论文地址：

https://arxiv.org/pdf/1905.09550.pdf

新智元春季招聘开启，一起弄潮 AI 之巅！

岗位详情请戳：