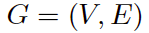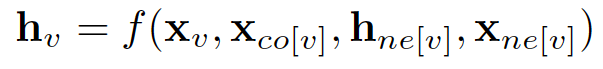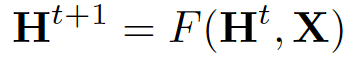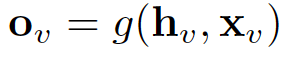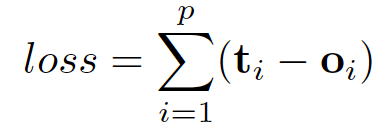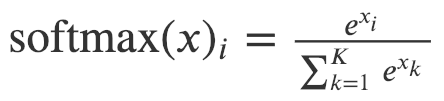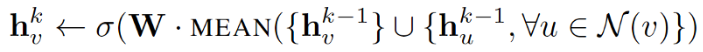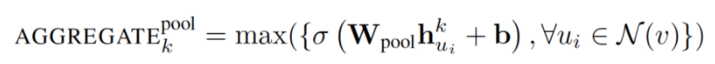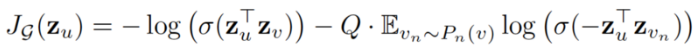掌握图神经网络GNN基本,看这篇文章就够了
新智元报道
来源:towardsdatascience
作者:黃功詳 Steeve Huang 编辑:肖琴
【新智元导读】图神经网络(GNN)在各个领域越来越受欢迎,本文介绍了图神经网络的基本知识,以及两种更高级的算法:DeepWalk和GraphSage。
最近,图神经网络 (GNN) 在各个领域越来越受到欢迎,包括社交网络、知识图谱、推荐系统,甚至生命科学。
GNN 在对图形中节点间的依赖关系进行建模方面能力强大,使得图分析相关的研究领域取得了突破性进展。本文旨在介绍图神经网络的基本知识,以及两种更高级的算法:DeepWalk 和 GraphSage。
在讨论 GNN 之前,让我们先了解一下什么是图 (Graph)。在计算机科学中,图是由两个部件组成的一种数据结构:顶点 (vertices) 和边 (edges)。一个图 G 可以用它包含的顶点 V 和边 E 的集合来描述。
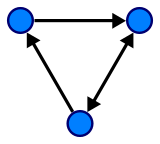
边可以是有向的或无向的,这取决于顶点之间是否存在方向依赖关系。
一个有向的图 (wiki)
顶点通常也被称为节点 (nodes)。在本文中,这两个术语是可以互换的。
图神经网络是一种直接在图结构上运行的神经网络。GNN 的一个典型应用是节点分类。本质上,图中的每个节点都与一个标签相关联,我们的目的是预测没有 ground-truth 的节点的标签。
本节将描述 The graph neural network model (Scarselli, F., et al., 2009) [1] 这篇论文中的算法,这是第一次提出 GNN 的论文,因此通常被认为是原始 GNN。
在节点分类问题设置中,每个节点 v 的特征 x_v 与一个 ground-truth 标签 t_v 相关联。给定一个部分标记的 graph G,目标是利用这些标记的节点来预测未标记的节点的标签。它学习用包含邻域信息的 d 维向量 h_v 表示每个节点。即:
其中 x_co[v] 表示与 v 相连的边的特征,h_ne[v] 表示 v 相邻节点的嵌入,x_ne[v] 表示v 相邻节点的特征。函数 f 是将这些输入映射到 d 维空间上的过渡函数。由于我们要寻找 h_v 的唯一解,我们可以应用 Banach 不动点定理,将上面的方程重写为一个迭代更新过程。
H 和 X 分别表示所有 h 和 x 的串联。
通过将状态 h_v 和特性 x_v 传递给输出函数 g,从而计算 GNN 的输出。
这里的 f 和 g 都可以解释为前馈全连接神经网络。L1 loss 可以直接表述为:
可以通过梯度下降进行优化。
然而,原始 GNN 存在三个主要局限性:
如果放宽 “不动点” (fixed point)的假设,那么可以利用多层感知器学习更稳定的表示,并删除迭代更新过程。这是因为,在原始论文中,不同的迭代使用转换函数 f 的相同参数,而 MLP 的不同层中的不同参数允许分层特征提取。
它不能处理边缘信息 (例如,知识图中的不同边缘可能表示节点之间的不同关系)
不动点会阻碍节点分布的多样性,不适合学习表示节点。
为了解决上述问题,研究人员已经提出了几个 GNN 的变体。不过,它们不是本文的重点。
DeepWalk [2] 是第一个提出以无监督的方式学习节点嵌入的算法。
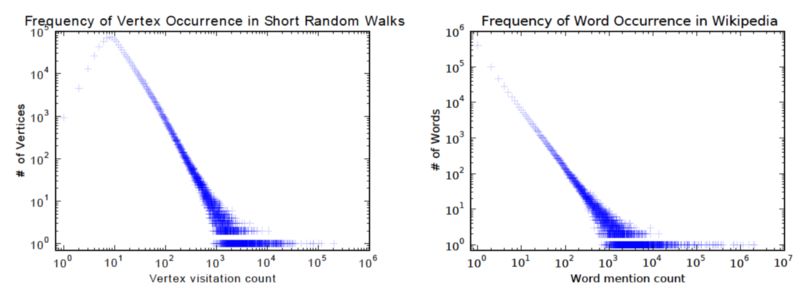
它在训练过程中非常类似于词汇嵌入。其动机是 graph 中节点和语料库中单词的分布都遵循幂律,如下图所示:
该算法包含两个步骤:
在 graph 中的节点上执行 random walks,以生成节点序列
运行 skip-gram,根据步骤 1 中生成的节点序列,学习每个节点的嵌入
在 random walks 的每个时间步骤中,下一个节点从上一个节点的邻节点均匀采样。然后将每个序列截断为长度为 2|w| + 1 的子序列,其中 w 表示 skip-gram 中的窗口大小。
本文采用 hierarchical softmax 来解决由于节点数量庞大而导致的 softmax 计算成本高昂的问题。为了计算每个单独输出元素的 softmax 值 , 我们必须计算元素 k 的所有 e ^ xk。
Softmax 的定义
因此,原始 softmax 的计算时间为 O(|V|),其中 V 表示图中顶点的集合。
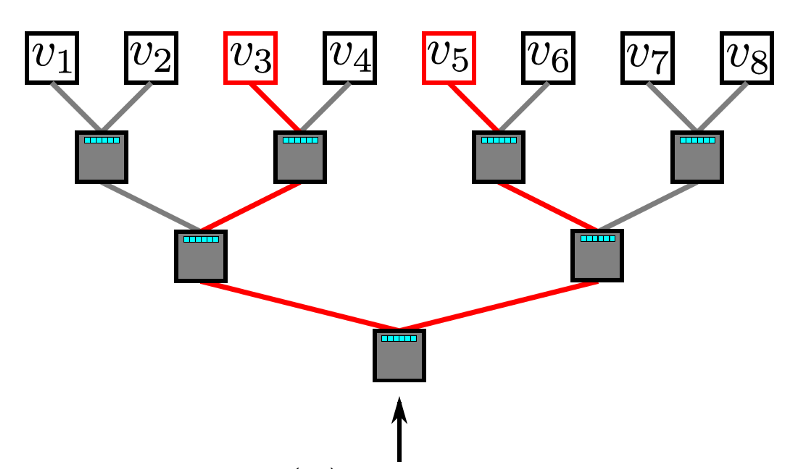
分层 softmax 利用二叉树来处理这个问题。在这个二叉树中,所有的叶子 (下图中的 v1, v2,…v8) 都表示 graph 中的顶点。在每个内部节点中,都有一个二元分类器来决定选择哪条路径。要计算给定顶点 v_k 的概率,只需计算从根节点到叶节点 v_k 路径上每一个子路径的概率。由于每个节点的子节点的概率之和为 1,所以所有顶点的概率之和为 1的特性在分层 softmax 中仍然保持不变。由于二叉树的最长路径是 O(log(n)),其中 n表示叶节点的数量,因此一个元素的计算时间现在减少到 O(log|V|)。
Hierarchical Softmax
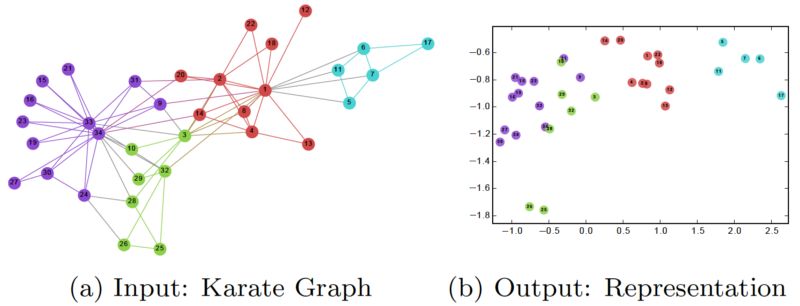
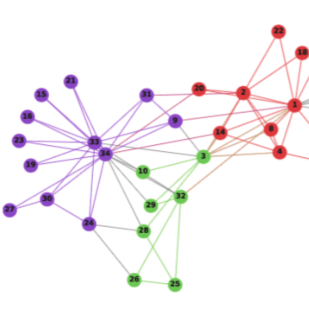
在训练完 DeepWalk GNN 之后,模型已经学习了每个节点的良好表示,如下图所示。不同的颜色表示输入图中的不同标签。我们可以看到,在输出图 (2 维嵌入) 中,具有相同标签的节点被聚集在一起,而具有不同标签的大多数节点都被正确地分开了。
然而,DeepWalk 的主要问题是缺乏泛化能力。每当一个新节点出现时,它必须重新训练模型以表示这个节点。因此,这种 GNN 不适用于图中节点不断变化的动态图。
GraphSage 提供了解决上述问题的办法,以一种归纳的方式学习每个节点的嵌入。
具体地说,GraphSage 每个节点由其邻域的聚合 (aggregation) 表示。因此,即使图中出现了在训练过程中没有看到的新节点,它仍然可以用它的邻近节点来恰当地表示。
下面是 GraphSage算法:
外层循环表示更新迭代的数量,而 h ^ k_v 表示更新迭代 k 时节点 v 的潜在向量。在每次更新迭代时,h ^ k_v 的更新基于一个聚合函数、前一次迭代中 v 和 v 的邻域的潜在向量,以及权重矩阵 W ^ k。
论文中提出了三种聚合函数:
1. Mean aggregator:
mean aggregator 取一个节点及其所有邻域的潜在向量的平均值。
与原始方程相比,它删除了上面伪代码中第 5 行中的连接运算。这种运算可以看作是一种 “skip-connection”,在论文后面的部分中,证明了这在很大程度上可以提高模型的性能。
2. LSTM aggregator:
由于图中的节点没有任何顺序,因此它们通过对这些节点进行排列来随机分配顺序。
3. Pooling aggregator:
这个运算符在相邻集上执行一个 element-wise 的 pooling 函数。下面是一个 max-pooling 的示例:
论文使用 max-pooling 作为默认的聚合函数。
损失函数定义如下:
其中 u 和 v 在固定长度的 random walk 中共存,而 v_n 是不与 u 共存的负样本。这种损失函数鼓励距离较近的节点具有相似的嵌入,而距离较远的节点则在投影空间中被分离。通过这种方法,节点将获得越来越多的关于其邻域的信息。
GraphSage 通过聚合其附近的节点,可以为看不见的节点生成可表示的嵌入。它允许将节点嵌入应用到涉及动态图的域,其中图的结构是不断变化的。例如,Pinterest 采用了GraphSage 的扩展版本 PinSage 作为其内容发现系统的核心。
本文中,我们学习了图神经网络、DeepWalk 和 GraphSage 的基础知识。GNN 在复杂图结构建模方面的强大功能确实令人惊叹。鉴于其有效性,我相信在不久的将来,GNN将在 AI 的发展中发挥重要作用。
[1] Scarselli, Franco, et al. "The graph neural network model.”
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.7227&rep=rep1&type=pdf
[2] Perozzi, Bryan, Rami Al-Rfou, and Steven Skiena. "Deepwalk: Online learning of social representations.”
http://www.perozzi.net/publications/14_kdd_deepwalk.pdf
[3] Hamilton, Will, Zhitao Ying, and Jure Leskovec. "Inductive representation learning on large graphs.”
https://www-cs-faculty.stanford.edu/people/jure/pubs/graphsage-nips17.pdf
更多阅读
点击“阅读原文”查看原文
【加入社群】
新智元AI技术+产业社群招募中,欢迎对AI技术+产业落地感兴趣的同学,加小助手微信号:aiera2015_2 入群;通过审核后我们将邀请进群,加入社群后务必修改群备注(姓名 - 公司 - 职位;专业群审核较严,敬请谅解)。