A monotone finite element method for an elliptic distributed optimal control problem with a convection-dominated state equation

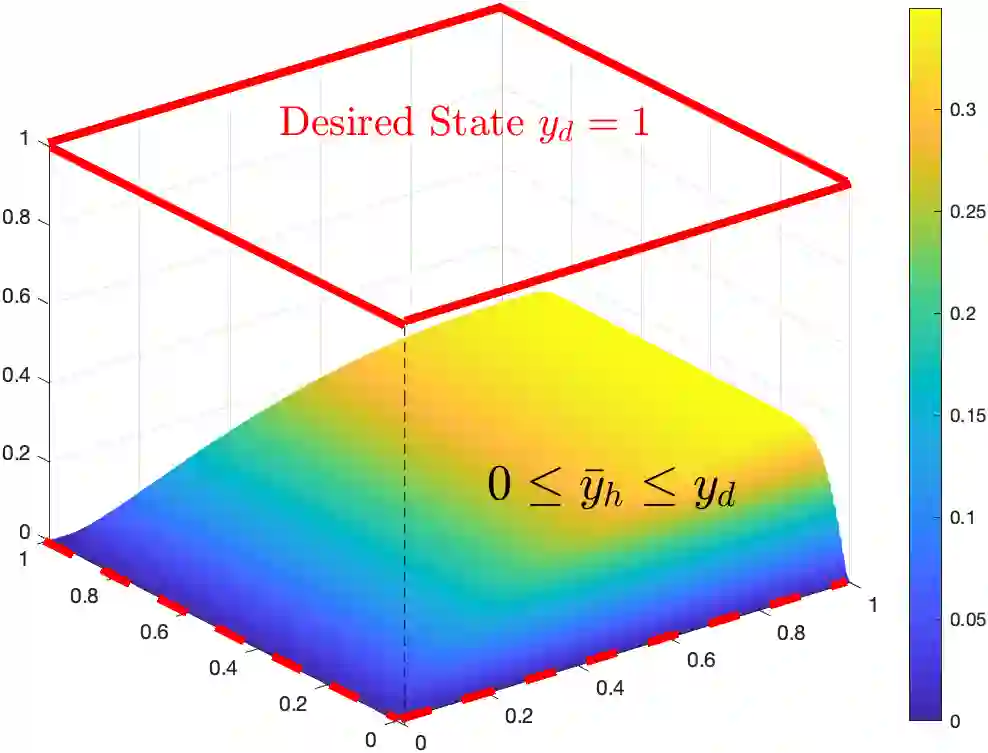
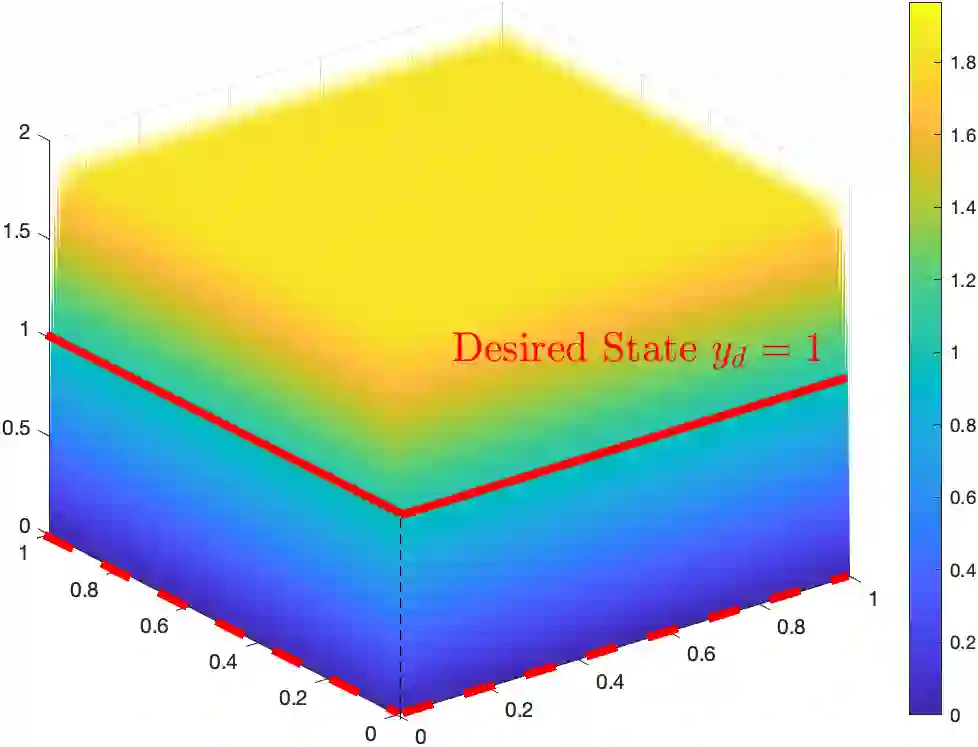
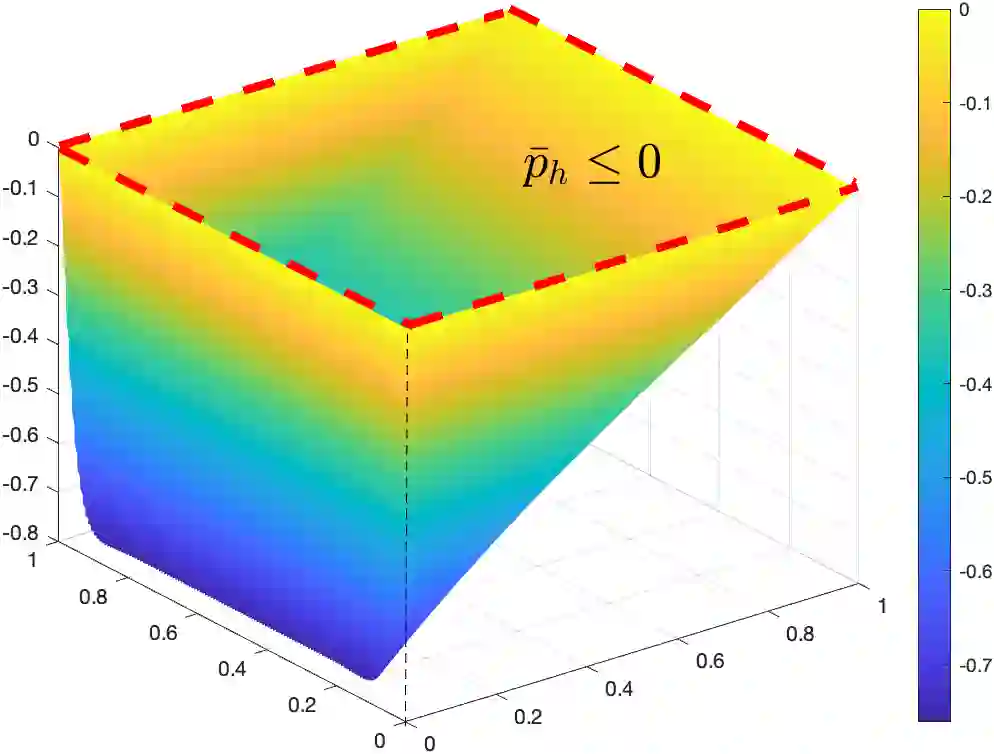
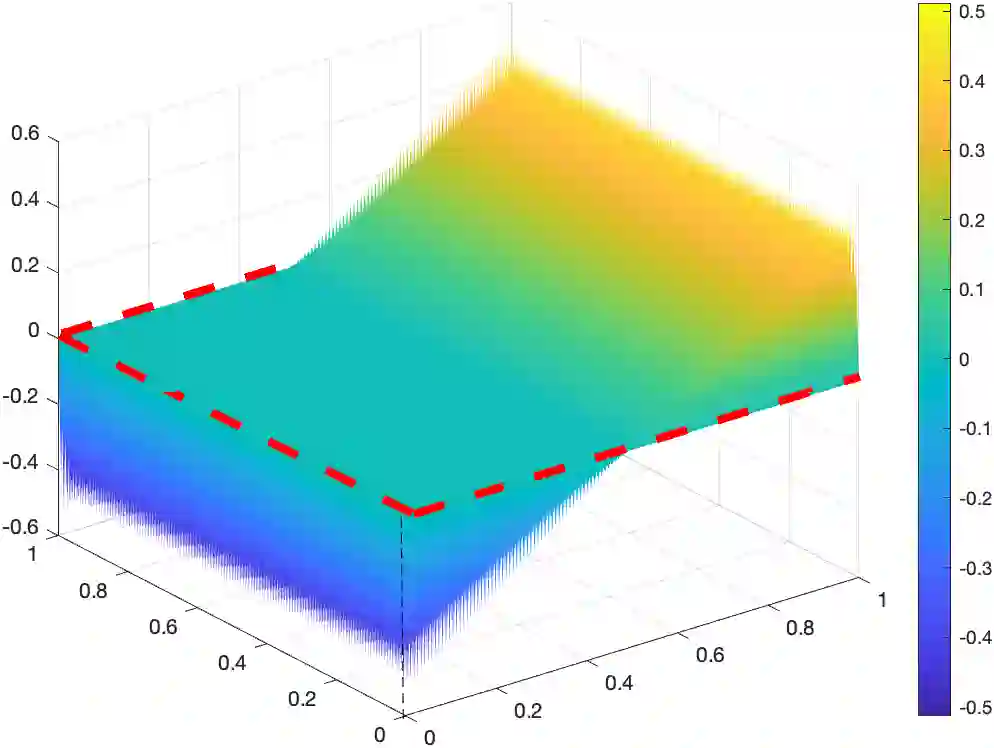
We propose and analyze a monotone finite element method for an elliptic distributed optimal control problem constrained by a convection-diffusion-reaction equation in the convection-dominated regime. The method is based on the edge-averaged finite element (EAFE) scheme, which is known to preserve the discrete maximum principle for convection-diffusion problems. We show that the EAFE discretization inherits the monotonicity property of the continuous problem and consequently preserves the desired-state bounds at the discrete level, ensuring that the numerical optimal state remains stable and free of nonphysical oscillations. The discrete formulation is analyzed using a combination of the EAFE consistency result and a discrete inf-sup condition, which together guarantee well-posedness and yield the optimal convergence order. Comprehensive numerical experiments are presented to confirm the theoretical findings and to demonstrate the robustness of the proposed scheme in the convection-dominated regimes.