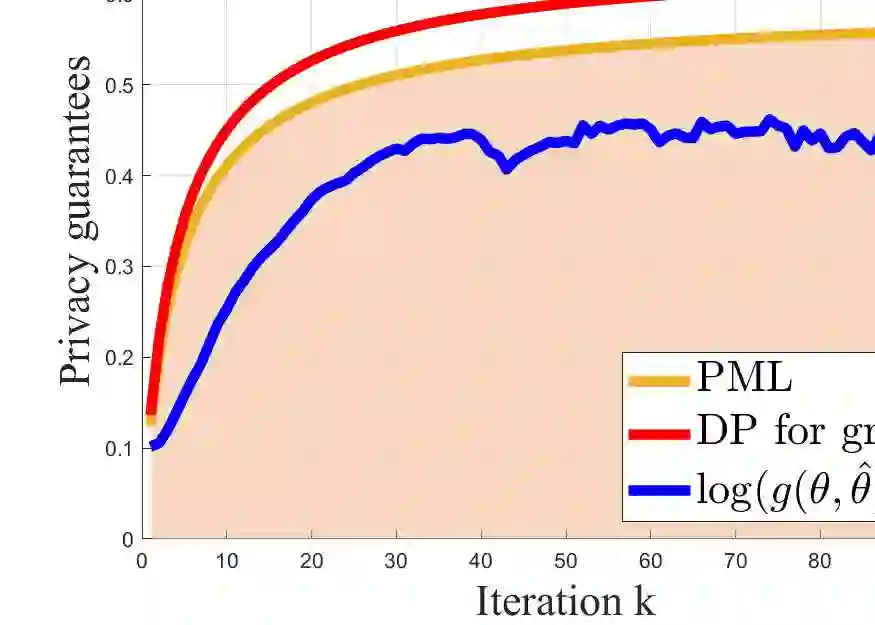
Privacy preservation has served as a key metric in designing Nash equilibrium (NE) computation algorithms. Although differential privacy (DP) has been widely employed for privacy guarantees, it does not exploit prior distributional knowledge of datasets and is ineffective in assessing information leakage for correlated datasets. To address these concerns, we establish a pointwise maximal leakage (PML) framework when computing NE in aggregative games. By incorporating prior knowledge of players' cost function datasets, we obtain a precise and computable upper bound of privacy leakage with PML guarantees. In the entire view, we show PML refines DP by offering a tighter privacy guarantee, enabling flexibility in designing NE computation. Also, in the individual view, we reveal that the lower bound of PML can exceed the upper bound of DP by constructing specific correlated datasets. The results emphasize that PML is a more proper privacy measure than DP since the latter fails to adequately capture privacy leakage in correlated datasets. Moreover, we conduct experiments with adversaries who attempt to infer players' private information to illustrate the effectiveness of our framework.
翻译:隐私保护已成为设计纳什均衡计算算法的关键指标。尽管差分隐私已被广泛用于提供隐私保障,但其未能利用数据集的先验分布知识,且在评估相关数据集的信息泄漏方面存在不足。为解决这些问题,我们在计算聚合博弈的纳什均衡时建立了一个逐点最大泄漏框架。通过纳入参与者成本函数数据集的先验知识,我们获得了具有PML保障的隐私泄漏的精确可计算上界。从整体视角看,我们证明PML通过提供更严格的隐私保障改进了差分隐私,为纳什均衡计算的设计提供了灵活性。同时,从个体视角看,我们通过构建特定的相关数据集,揭示了PML的下界可能超过差分隐私的上界。这些结果强调PML是比差分隐私更合适的隐私度量,因为后者未能充分捕捉相关数据集中的隐私泄漏。此外,我们通过模拟试图推断参与者私有信息的对手进行了实验,以说明我们框架的有效性。