Walking in the Shadow: A New Perspective on Descent Directions for Constrained Minimization

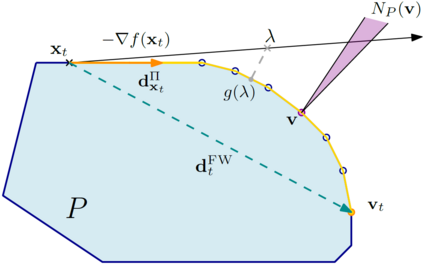
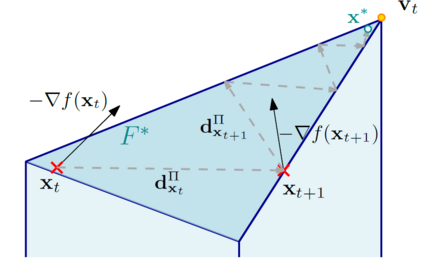
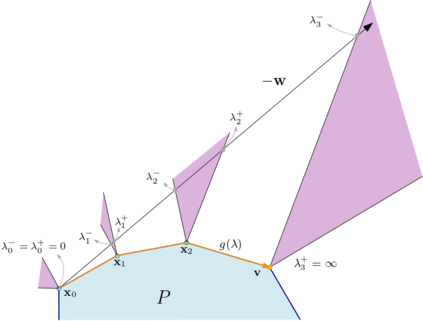
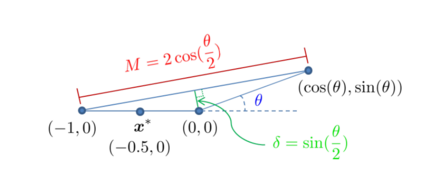
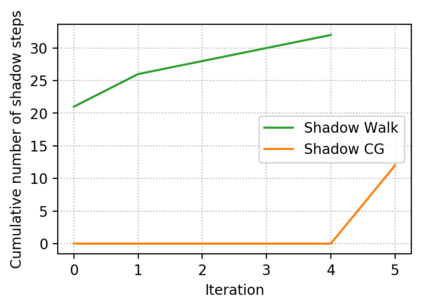
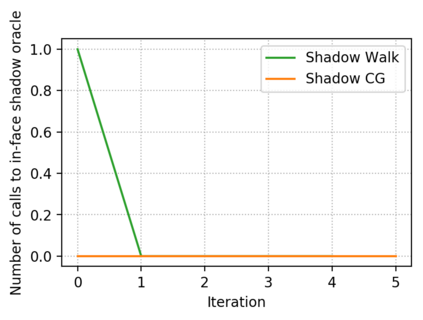
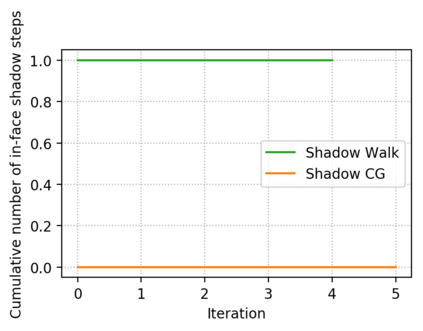
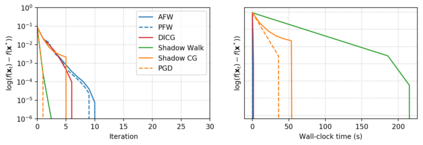
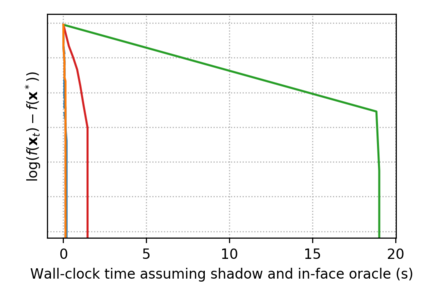
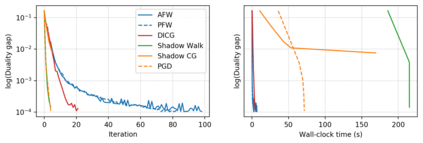
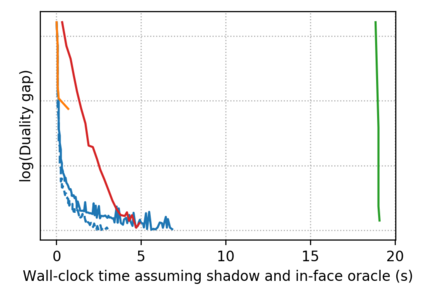
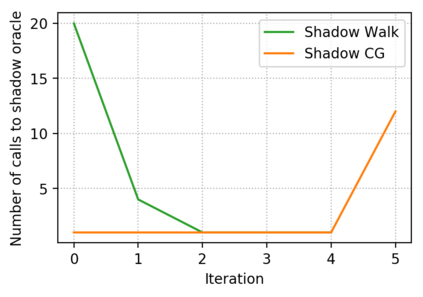
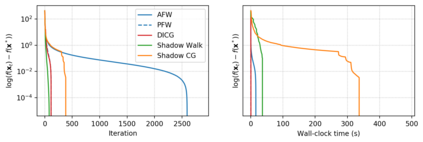
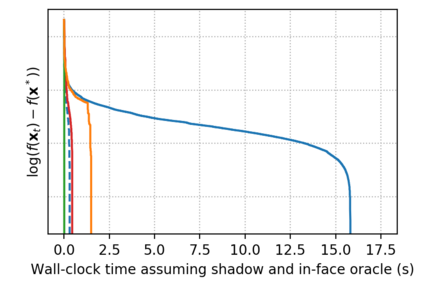
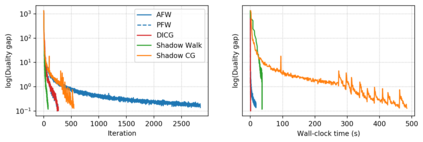
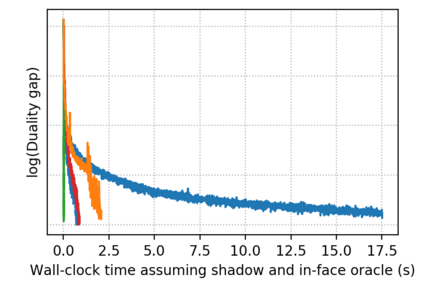
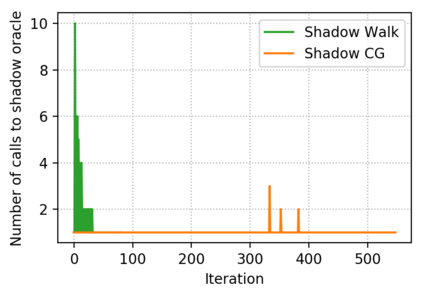
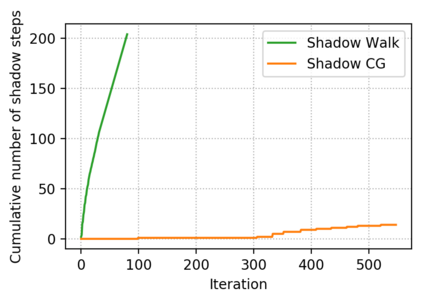
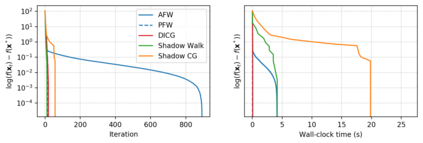
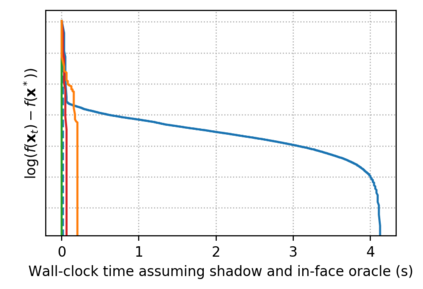
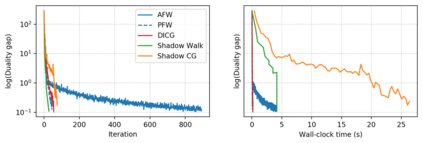
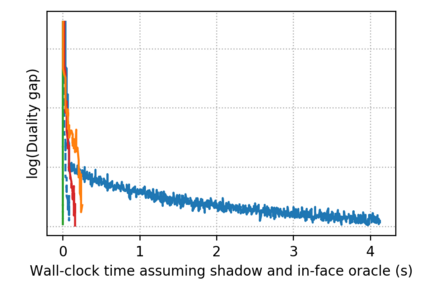
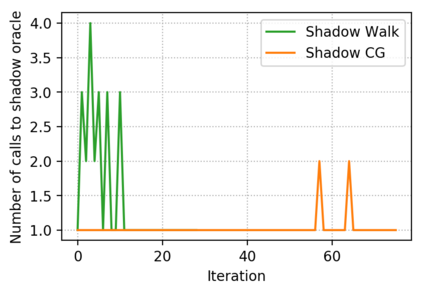
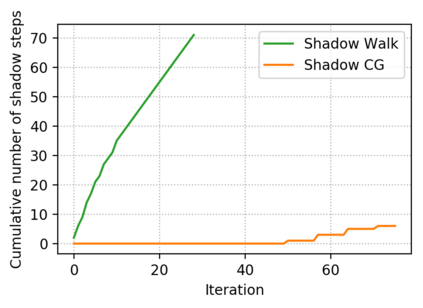
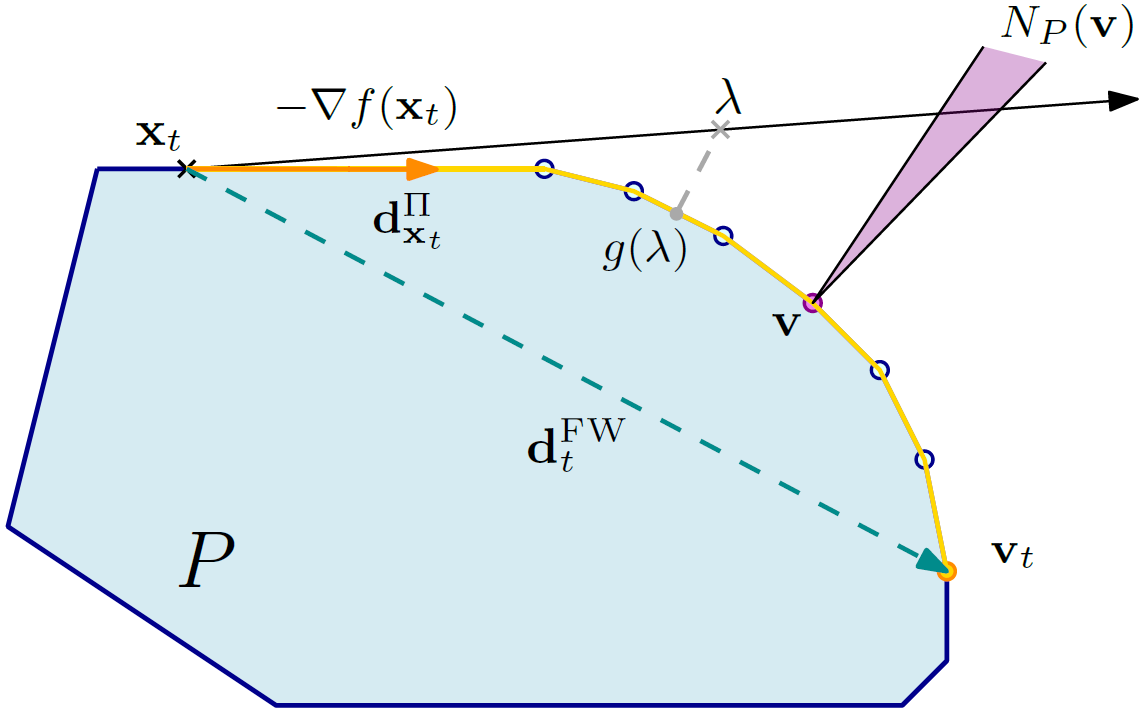
Descent directions such as movement towards Frank-Wolfe vertices, away steps, in-face away steps and pairwise directions have been an important design consideration in conditional gradient descent (CGD) variants. In this work, we attempt to demystify the impact of movement in these directions towards attaining constrained minimizers. The best local direction of descent is the directional derivative of the projection of the gradient, which we refer to as the $\textit{shadow}$ of the gradient. We show that the continuous-time dynamics of moving in the shadow are equivalent to those of PGD however non-trivial to discretize. By projecting gradients in PGD, one not only ensures feasibility but also is able to "wrap" around the convex region. We show that Frank-Wolfe (FW) vertices in fact recover the maximal wrap one can obtain by projecting gradients, thus providing a new perspective to these steps. We also claim that the shadow steps give the best direction of descent emanating from the convex hull of all possible away-vertices. Opening up the PGD movements in terms of shadow steps gives linear convergence, dependent on the number of faces. We combine these insights into a novel $S\small{HADOW}$-$CG$ method that uses FW steps (i.e., wrap around the polytope) and shadow steps (i.e., optimal local descent direction), while enjoying linear convergence. Our analysis develops properties of directional derivatives of projections (which may be of independent interest), while providing a unifying view of various descent directions in the CGD literature.