Gaussian Process-based calculation of look-elsewhere trials factor

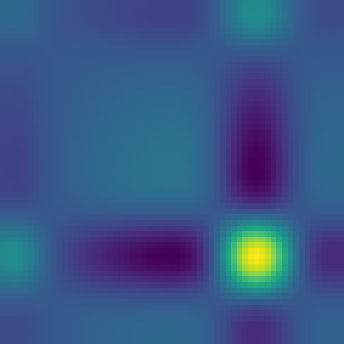
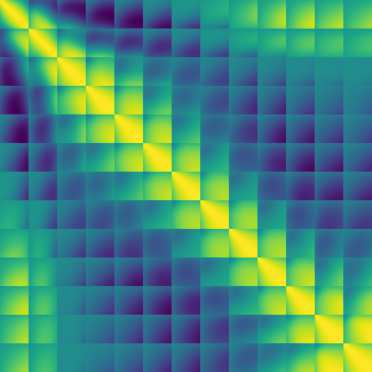
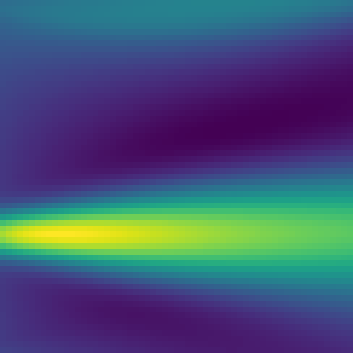
In high-energy physics it is a recurring challenge to efficiently and precisely (enough) calculate the global significance of, e.g., a potential new resonance. The Gross and Vitells trials factor approximation [arXiv:1105.4355(3)] and [arXiv:1105.4355(1)], which is based on the average expected "up-crossings" of the significance in the search region, has revolutionized this for significances above 3 standard deviations, but the challenges of actually calculating the average expected up-crossings and the validity of the approximation for smaller significances remain. We propose a new method that models the significance in the search region as a Gaussian Process (GP). The covariance matrix of the GP is calculated with a carefully designed set of Asimov background-only data sets, comparable in number to the random background-only data sets used in a typical analysis, however, the average up-crossings (and even directly the trials factor for both low and moderate significances) can subsequently be calculated to the desired precision with a computationally inexpensive random sampling of the GP. Once the covariance of the GP is determined, the average number of up-crossings can be computed analytically. In our work we give some highlights of the analytic calculation and also discuss some peculiarities of the trials factor estimation on a finite grid. We illustrate the method with studies of three complementary statistical models, including the one studied by Gross and Vitells [arXiv:1105.4355(3)].