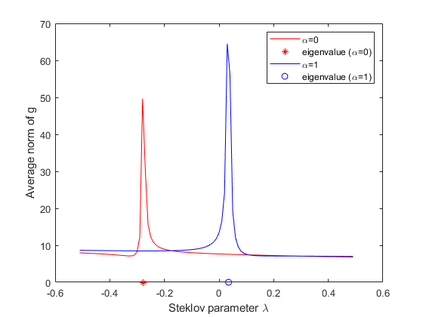
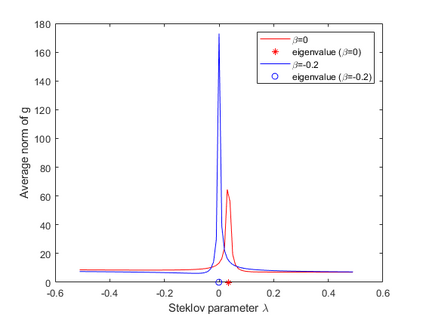
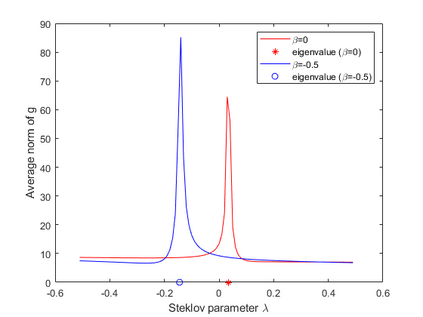
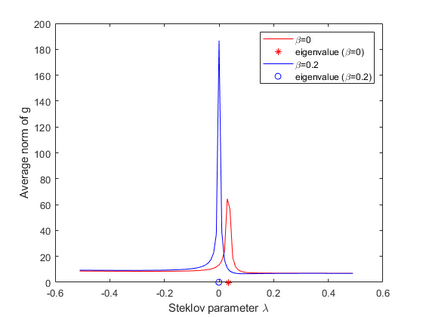
We investigate an inverse scattering problem for a thin inhomogeneous scatterer in R^m, m = 2,3, which we model as a m-1 dimensional open surface. The scatterer is referred to as a screen. The goal is to design target signatures that are computable from scattering data in order to detect changes in the material properties of the screen. This target signature is characterized by a mixed Steklov eigenvalue problem for a domain whose boundary contains the screen. We show that the corresponding eigenvalues can be determined from appropriately modified scattering data by using the generalized linear sampling method. A weaker justification is provided for the classical linear sampling method. Numerical experiments are presented to support our theoretical results.
翻译:我们在R ⁇ m m = 2,3, 我们用一个 m-1 维的开放表面模型来模拟一个薄异质散射器的反向散射问题。 散射器称为屏幕。 目标是设计从散射数据中可计算的目标信号, 以便检测屏幕物质特性的变化。 这个目标信号的特点是边界包含屏幕的域存在一个混合的Steklov 电子元值问题。 我们通过使用通用线性取样方法, 显示相应的电子元值可以通过适当修改的散射数据来确定。 经典线性取样方法有一个较弱的理由。 提供了数字实验来支持我们的理论结果。