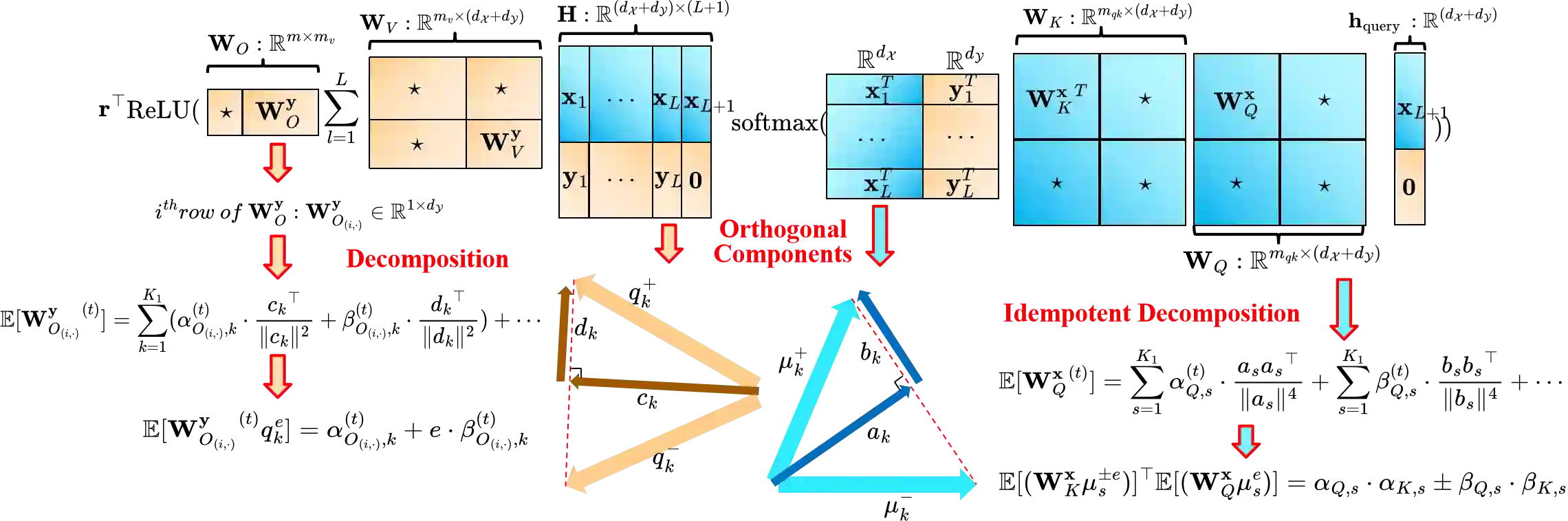
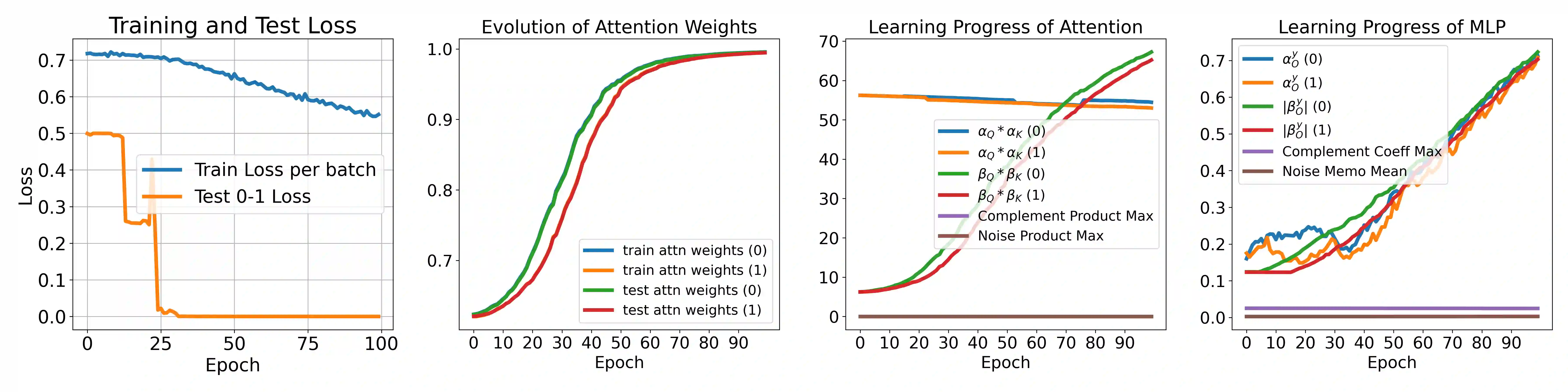
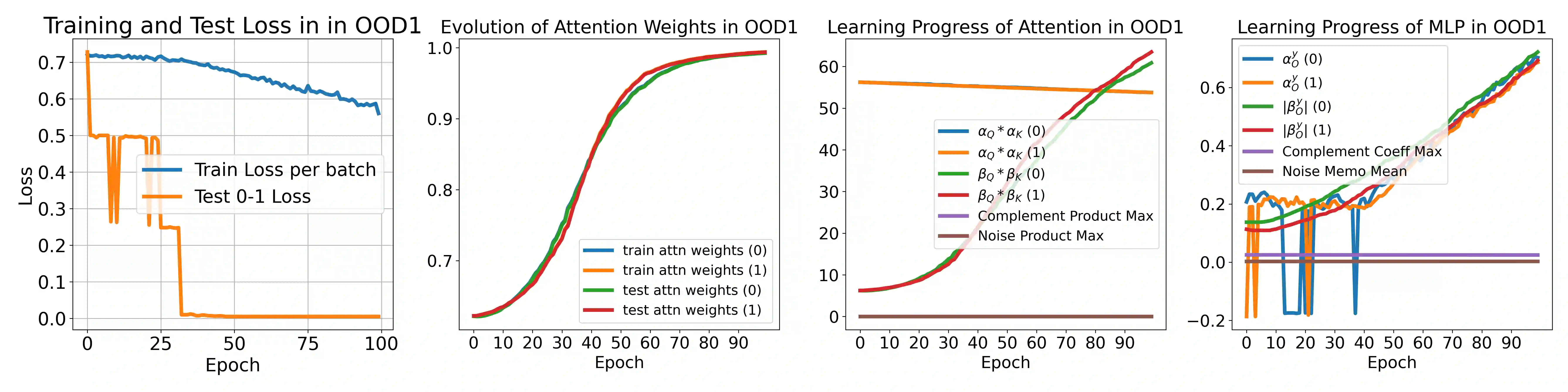
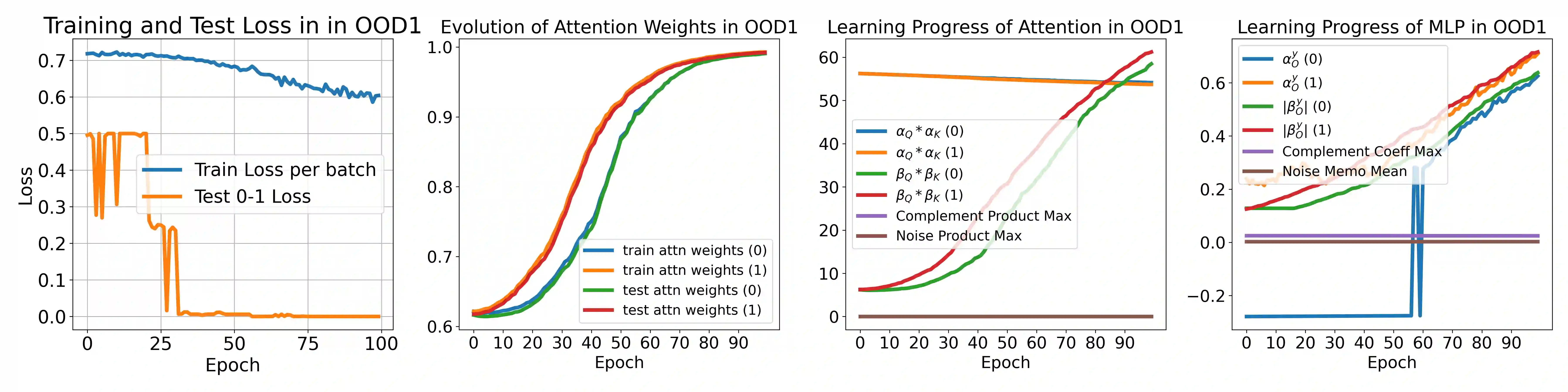
Transformer-based large language models (LLMs) have displayed remarkable creative prowess and emergence capabilities. Existing empirical studies have revealed a strong connection between these LLMs' impressive emergence abilities and their in-context learning (ICL) capacity, allowing them to solve new tasks using only task-specific prompts without further fine-tuning. On the other hand, existing empirical and theoretical studies also show that there is a linear regularity of the multi-concept encoded semantic representation behind transformer-based LLMs. However, existing theoretical work fail to build up an understanding of the connection between this regularity and the innovative power of ICL. Additionally, prior work often focuses on simplified, unrealistic scenarios involving linear transformers or unrealistic loss functions, and they achieve only linear or sub-linear convergence rates. In contrast, this work provides a fine-grained mathematical analysis to show how transformers leverage the multi-concept semantics of words to enable powerful ICL and excellent out-of-distribution ICL abilities, offering insights into how transformers innovate solutions for certain unseen tasks encoded with multiple cross-concept semantics. Inspired by empirical studies on the linear latent geometry of LLMs, the analysis is based on a concept-based low-noise sparse coding prompt model. Leveraging advanced techniques, this work showcases the exponential 0-1 loss convergence over the highly non-convex training dynamics, which pioneeringly incorporates the challenges of softmax self-attention, ReLU-activated MLPs, and cross-entropy loss. Empirical simulations corroborate the theoretical findings.
翻译:暂无翻译