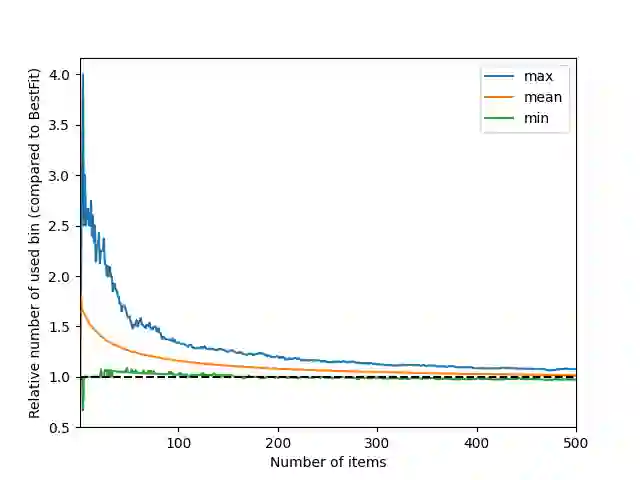
Recent studies have suggested that Large Language Models (LLMs) could provide interesting ideas contributing to mathematical discovery. This claim was motivated by reports that LLM-based genetic algorithms produced heuristics offering new insights into the online bin packing problem under uniform and Weibull distributions. In this work, we reassess this claim through a detailed analysis of the heuristics produced by LLMs, examining both their behavior and interpretability. Despite being human-readable, these heuristics remain largely opaque even to domain experts. Building on this analysis, we propose a new class of algorithms tailored to these specific bin packing instances. The derived algorithms are significantly simpler, more efficient, more interpretable, and more generalizable, suggesting that the considered instances are themselves relatively simple. We then discuss the limitations of the claim regarding LLMs' contribution to this problem, which appears to rest on the mistaken assumption that the instances had previously been studied. Our findings instead emphasize the need for rigorous validation and contextualization when assessing the scientific value of LLM-generated outputs.
翻译:近期研究表明,大型语言模型(LLMs)可能为数学发现提供有价值的思路。这一主张源于基于LLM的遗传算法在均匀分布和威布尔分布下的在线装箱问题中,产生了具有新启发意义的启发式方法。本研究通过对LLM生成的启发式方法进行详细分析,重新评估了这一主张,考察了其行为特征与可解释性。尽管这些启发式方法具备人类可读性,但即使对领域专家而言,其内在机制仍高度不透明。基于此分析,我们提出了一类针对特定装箱问题实例的新型算法。所推导的算法显著更简洁、高效、可解释且泛化能力更强,表明所考察的问题实例本身相对简单。随后,我们讨论了关于LLM对该问题贡献主张的局限性,该主张似乎建立在错误假设之上,即相关实例先前已被充分研究。我们的研究结果强调,在评估LLM生成输出的科学价值时,必须进行严格验证与情境化分析。