Encrypted Distributed Lasso for Sparse Data Predictive Control

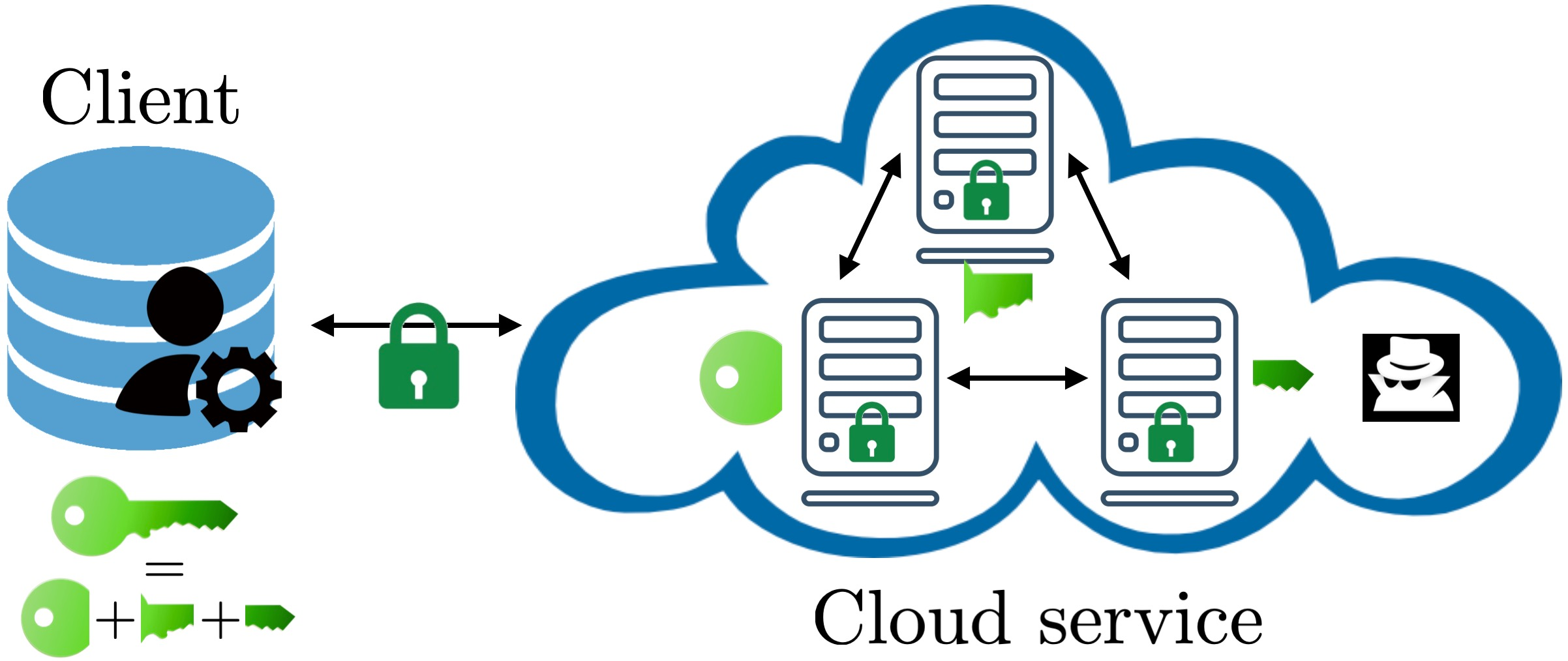
The least squares problem with L1-regularized regressors, called Lasso, is a widely used approach in optimization problems where sparsity of the regressors is desired. This formulation is fundamental for many applications in signal processing, machine learning and control. As a motivating problem, we investigate a sparse data predictive control problem, run at a cloud service to control a system with unknown model, using L1-regularization to limit the behavior complexity. The input-output data collected for the system is privacy-sensitive, hence, we design a privacy-preserving solution using homomorphically encrypted data. The main challenges are the non-smoothness of the L1-norm, which is difficult to evaluate on encrypted data, as well as the iterative nature of the Lasso problem. We use a distributed ADMM formulation that enables us to exchange substantial local computation for little communication between multiple servers. We first give an encrypted multi-party protocol for solving the distributed Lasso problem, by approximating the non-smooth part with a Chebyshev polynomial, evaluating it on encrypted data, and using a more cost effective distributed bootstrapping operation. For the example of data predictive control, we prefer a non-homogeneous splitting of the data for better convergence. We give an encrypted multi-party protocol for this non-homogeneous splitting of the Lasso problem to a non-homogeneous set of servers: one powerful server and a few less powerful devices, added for security reasons. Finally, we provide numerical results for our proposed solutions.