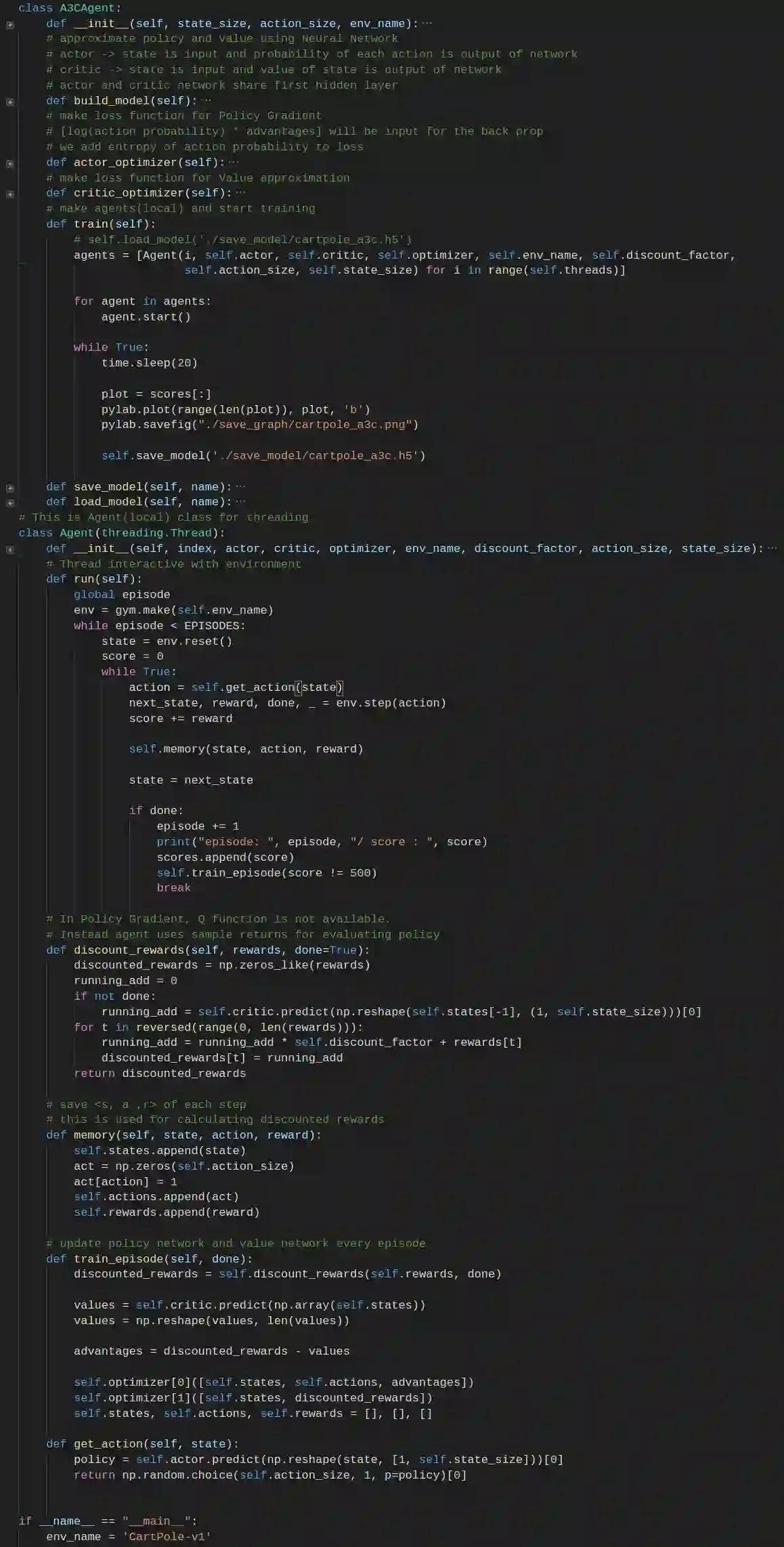
强化学习 cartpole_a3c

https://github.com/rlcode/reinforcement-learning/blob/master/2-cartpole/5-a3c/cartpole_a3c.py

import threading

import numpy as np

import tensorflow as tf

import pylab

import time

import gym

from keras.layers import Dense, Input

from keras.models import Model

from keras.optimizers import Adam

from keras import backend as K

# global variables for threading

episode = 0

scores = []

EPISODES = 2000

# This is A3C(Asynchronous Advantage Actor Critic) agent(global) for the Cartpole

# In this example, we use A3C algorithm

class A3CAgent:

def __init__(self, state_size, action_size, env_name):

# get size of state and action

self.state_size = state_size

self.action_size = action_size

# get gym environment name

self.env_name = env_name

# these are hyper parameters for the A3C

self.actor_lr = 0.001

self.critic_lr = 0.001

self.discount_factor = .99

self.hidden1, self.hidden2 = 24, 24

self.threads = 8

# create model for actor and critic network

self.actor, self.critic = self.build_model()

# method for training actor and critic network

self.optimizer = [self.actor_optimizer(), self.critic_optimizer()]

self.sess = tf.InteractiveSession()

K.set_session(self.sess)

self.sess.run(tf.global_variables_initializer())

# approximate policy and value using Neural Network

# actor -> state is input and probability of each action is output of network

# critic -> state is input and value of state is output of network

# actor and critic network share first hidden layer

def build_model(self):

state = Input(batch_shape=(None,  self.state_size))

shared = Dense(self.hidden1, input_dim=self.state_size, activation='relu', kernel_initializer='glorot_uniform')(state)

actor_hidden = Dense(self.hidden2, activation='relu', kernel_initializer='glorot_uniform')(shared)

action_prob = Dense(self.action_size, activation='softmax', kernel_initializer='glorot_uniform')(actor_hidden)

value_hidden = Dense(self.hidden2, activation='relu', kernel_initializer='he_uniform')(shared)

state_value = Dense(1, activation='linear', kernel_initializer='he_uniform')(value_hidden)

actor = Model(inputs=state, outputs=action_prob)

critic = Model(inputs=state, outputs=state_value)

actor._make_predict_function()

critic._make_predict_function()

actor.summary()

critic.summary()

return actor, critic

# make loss function for Policy Gradient

# [log(action probability) * advantages] will be input for the back prop

# we add entropy of action probability to loss

def actor_optimizer(self):

action = K.placeholder(shape=(None, self.action_size))

advantages = K.placeholder(shape=(None, ))

policy = self.actor.output

good_prob = K.sum(action * policy, axis=1)

eligibility = K.log(good_prob + 1e-10) * K.stop_gradient(advantages)

loss = -K.sum(eligibility)

entropy = K.sum(policy * K.log(policy + 1e-10), axis=1)

actor_loss = loss + 0.01*entropy

optimizer = Adam(lr=self.actor_lr)

updates = optimizer.get_updates(self.actor.trainable_weights, [], actor_loss)

train = K.function([self.actor.input, action, advantages], [], updates=updates)

return train

# make loss function for Value approximation

def critic_optimizer(self):

discounted_reward = K.placeholder(shape=(None, ))

value = self.critic.output

loss = K.mean(K.square(discounted_reward - value))

optimizer = Adam(lr=self.critic_lr)

updates = optimizer.get_updates(self.critic.trainable_weights, [], loss)

train = K.function([self.critic.input, discounted_reward], [], updates=updates)

return train

# make agents(local) and start training

def train(self):

# self.load_model('./save_model/cartpole_a3c.h5')

agents = [Agent(i, self.actor, self.critic, self.optimizer, self.env_name, self.discount_factor,

self.action_size, self.state_size) for i in range(self.threads)]

for agent in agents:

agent.start()

while True:

time.sleep(20)

plot = scores[:]

pylab.plot(range(len(plot)), plot, 'b')

pylab.savefig("./save_graph/cartpole_a3c.png")

self.save_model('./save_model/cartpole_a3c.h5')

def save_model(self, name):

self.actor.save_weights(name + "_actor.h5")

self.critic.save_weights(name + "_critic.h5")

def load_model(self, name):

self.actor.load_weights(name + "_actor.h5")

self.critic.load_weights(name + "_critic.h5")

# This is Agent(local) class for threading

class Agent(threading.Thread):

def __init__(self, index, actor, critic, optimizer, env_name, discount_factor, action_size, state_size):

threading.Thread.__init__(self)

self.states = []

self.rewards = []

self.actions = []

self.index = index

self.actor = actor

self.critic = critic

self.optimizer = optimizer

self.env_name = env_name

self.discount_factor = discount_factor

self.action_size = action_size

self.state_size = state_size

# Thread interactive with environment

def run(self):

global episode

env = gym.make(self.env_name)

while episode < EPISODES:

state = env.reset()

score = 0

while True:

action = self.get_action(state)

next_state, reward, done, _ = env.step(action)

score += reward

self.memory(state, action, reward)

state = next_state

if done:

episode += 1

print("episode: ", episode, "/ score : ", score)

scores.append(score)

self.train_episode(score != 500)

break

# In Policy Gradient, Q function is not available.

# Instead agent uses sample returns for evaluating policy

def discount_rewards(self, rewards, done=True):

discounted_rewards = np.zeros_like(rewards)

running_add = 0

if not done:

running_add = self.critic.predict(np.reshape(self.states[-1], (1, self.state_size)))[0]

for t in reversed(range(0, len(rewards))):

running_add = running_add * self.discount_factor + rewards[t]

discounted_rewards[t] = running_add

return discounted_rewards

# save <s, a ,r> of each step

# this is used for calculating discounted rewards

def memory(self, state, action, reward):

self.states.append(state)

act = np.zeros(self.action_size)

act[action] = 1

self.actions.append(act)

self.rewards.append(reward)

# update policy network and value network every episode

def train_episode(self, done):

discounted_rewards = self.discount_rewards(self.rewards, done)

values = self.critic.predict(np.array(self.states))

values = np.reshape(values, len(values))

advantages = discounted_rewards - values

self.optimizer[0]([self.states, self.actions, advantages])

self.optimizer[1]([self.states, discounted_rewards])

self.states, self.actions, self.rewards = [], [], []

def get_action(self, state):

policy = self.actor.predict(np.reshape(state, [1, self.state_size]))[0]

return np.random.choice(self.action_size, 1, p=policy)[0]

if __name__ == "__main__":

env_name = 'CartPole-v1'

env = gym.make(env_name)

state_size = env.observation_space.shape[0]

action_size = env.action_space.n

env.close()

global_agent = A3CAgent(state_size, action_size, env_name)

global_agent.train()