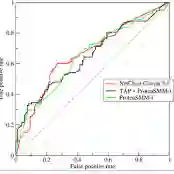
The ROC curve is widely used to assess binary classification performance. Yet for some applications such as alert systems for hospitalized patient monitoring, conventional ROC analysis cannot capture crucial factors that impact deployment, such as enforcing a minimum precision constraint to avoid false alarm fatigue or imposing an upper bound on the number of predicted positives to represent the capacity of hospital staff. The usual area under the curve metric also does not reflect asymmetric costs for false positives and false negatives. In this paper we address all three of these issues. First, we show how the subset of classifiers that meet given precision and capacity constraints can be represented as a feasible region in ROC space. We establish the geometry of this feasible region. We then define the partial area of lesser classifiers, a performance metric that is monotonic with cost and only accounts for the feasible portion of ROC space. Averaging this area over a desired range of cost parameters results in the partial volume over the ROC surface, or partial VOROS. In experiments predicting mortality risk using vital sign history on the MIMIC-IV dataset, we show this cost-aware metric is better than alternatives for ranking classifiers in hospital alert applications.
翻译:ROC曲线被广泛用于评估二元分类性能。然而,对于某些应用(如住院患者监测的警报系统),传统的ROC分析无法捕捉影响部署的关键因素,例如强制设定最小精度约束以避免误报疲劳,或对预测阳性数量设定上限以反映医护人员的工作容量。传统的曲线下面积度量同样无法反映假阳性与假阴性的非对称成本。本文同时解决了这三个问题。首先,我们展示了如何将满足给定精度与容量约束的分类器子集表示为ROC空间中的可行区域,并建立了该可行区域的几何结构。随后,我们定义了"次优分类器部分面积"这一性能度量,该度量与成本呈单调关系且仅考虑ROC空间的可行部分。将此面积在目标成本参数范围内进行平均,即得到ROC曲面上的部分体积,称为部分VOROS。在使用MIMIC-IV数据集基于生命体征历史预测死亡风险的实验中,我们证明这种成本感知度量在医院警报应用的分类器排序中优于其他替代方法。