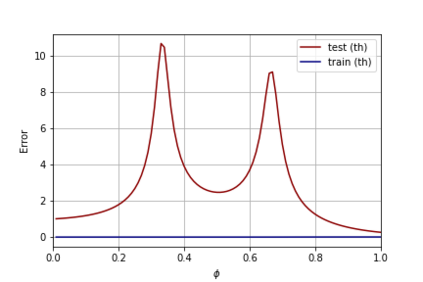
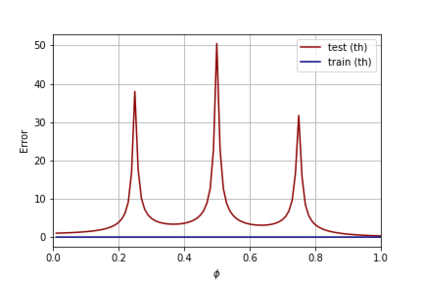
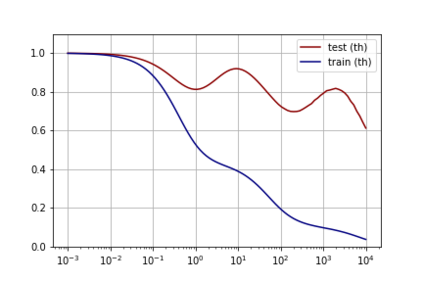
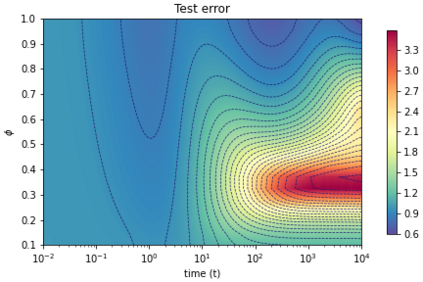
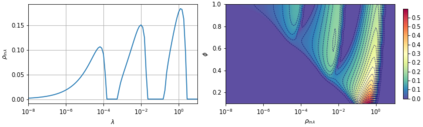
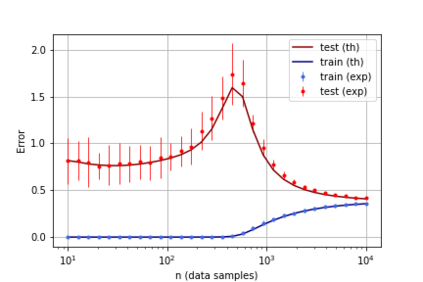
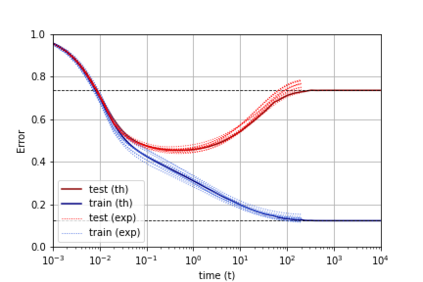
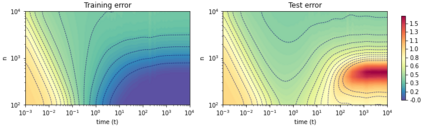
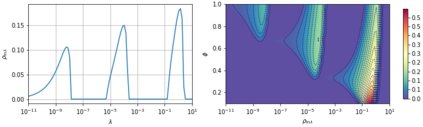
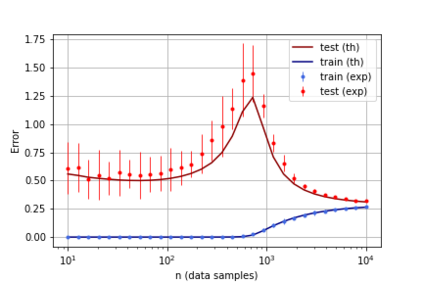
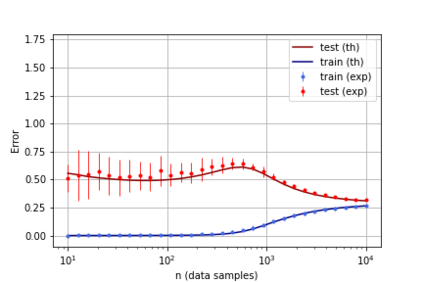
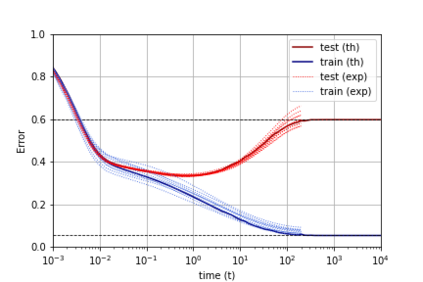
A recent line of work has shown remarkable behaviors of the generalization error curves in simple learning models. Even the least-squares regression has shown atypical features such as the model-wise double descent, and further works have observed triple or multiple descents. Another important characteristic are the epoch-wise descent structures which emerge during training. The observations of model-wise and epoch-wise descents have been analytically derived in limited theoretical settings (such as the random feature model) and are otherwise experimental. In this work, we provide a full and unified analysis of the whole time-evolution of the generalization curve, in the asymptotic large-dimensional regime and under gradient-flow, within a wider theoretical setting stemming from a gaussian covariate model. In particular, we cover most cases already disparately observed in the literature, and also provide examples of the existence of multiple descent structures as a function of a model parameter or time. Furthermore, we show that our theoretical predictions adequately match the learning curves obtained by gradient descent over realistic datasets. Technically we compute averages of rational expressions involving random matrices using recent developments in random matrix theory based on "linear pencils". Another contribution, which is also of independent interest in random matrix theory, is a new derivation of related fixed point equations (and an extension there-off) using Dyson brownian motions.
翻译:最近的一行工作展示了简单学习模型中一般化误差曲线的显著行为。即使是最不光彩的回归也显示了典型的特征,如模型的双向双向下降,进一步的工程也观察到了三或多种下降。另一个重要特征是培训过程中出现的先入为主的血统结构。从分析角度从有限的理论环境(如随机特征模型)中得出了对模型和先入为主的血统的观察,并进行了其他实验。在这项工作中,我们对一般化曲线的整个时间演变、无症状的大维系统和梯度流中,显示了非典型的特征,如模型双向双向双向的双向下降,并观察到了三或多向的下降。另一个重要特征是培训过程中出现的先入为主的世血统结构结构。此外,我们展示了我们的理论预测与在现实数据集中以渐渐渐下降为主的学习曲线完全吻合。技术方面,我们用离子大系统和梯流下流的理性表达方式进行了全面和统一分析,这些表达方式来自一个由高清的理论模型和离差的模型模型模型中的最新矩阵模型。