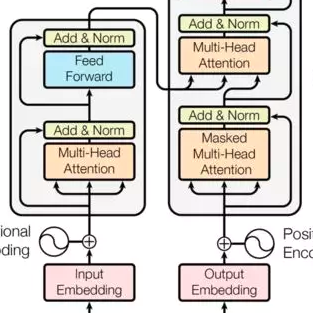
Transformer是谷歌发表的论文《Attention Is All You Need》提出一种完全基于Attention的翻译架构
知识荟萃
论文列表
原文：
- 《Attention is all you need》：https://papers.nips.cc/paper/7181-attention-is-all-you-need.pdf
相关论文
- 《Reformer: The Efficient Transformer》：https://arxiv.org/abs/2001.04451
开源代码
- Kyubyong/transformer (TF)
- huggingface/transformers (PyTorch)
VIP内容
少样本分类的目的是在只有少量样本的情况下识别不可见的类。我们考虑了多域少样本图像分类的问题，其中不可见的类和例子来自不同的数据源。人们对这个问题越来越感兴趣，并激发了元数据集等基准的开发。在这种多领域设置的一个关键挑战是有效地整合来自不同训练领域集的特征表示。在这里，我们提出了一个通用表示Transformer(URT)层，该元学会通过动态地重新加权和组合最合适的特定于领域的表示来利用通用特性进行少样本分类。在实验中，我们表明，URT在元数据集上设置了一个新的最先进的结果。具体来说，与竞争方法相比，它在数据源数量最多的情况下实现了最佳性能。我们分析了URT的各种变体，并给出了一个可视化的注意力分数热图，以阐明该模型是如何执行跨领域泛化的。
https://www.zhuanzhi.ai/paper/40930a0aff223a2d2baab3d1d92d7674
成为VIP会员查看完整内容
A Universal Representation Transformer Layer for Few-Shot Image Classification
热门内容
最新内容
最新论文
In this paper, we consider the use of Total Variation (TV) minimization for compressive imaging; that is, image reconstruction from subsampled measurements. Focusing on two important imaging modalities -- namely, Fourier imaging and structured binary imaging via the Walsh--Hadamard transform -- we derive uniform recovery guarantees asserting stable and robust recovery for arbitrary random sampling strategies. Using this, we then derive a class of theoretically-optimal sampling strategies. For Fourier sampling, we show recovery of an image with approximately $s$-sparse gradient from $m \gtrsim_d s \cdot \log^2(s) \cdot \log^4(N)$ measurements, in $d \geq 1$ dimensions. When $d = 2$, this improves the current state-of-the-art result by a factor of $\log(s) \cdot \log(N)$. It also extends it to arbitrary dimensions $d \geq 2$. For Walsh sampling, we prove that $m \gtrsim_d s \cdot \log^2(s) \cdot \log^2(N/s) \cdot \log^3(N) $ measurements suffice in $d \geq 2$ dimensions. To the best of our knowledge, this is the first recovery guarantee for structured binary sampling with TV minimization.
