【ICML2025教程】联想记忆的现代方法

摘要

联想记忆（Associative Memories），如著名的霍普菲尔德网络（Hopfield Networks），是一类优雅的模型，用于描述全连接递归神经网络，其核心任务是存储和检索信息。近年来，随着关于其信息存储能力的新理论成果的涌现，以及它们与当前最先进的人工智能架构（如 Transformer 和扩散模型）之间关系的发现，联想记忆重新获得了研究者的广泛关注。这些联系为通过联想记忆的理论视角解释传统 AI 网络的计算过程打开了新可能。 此外，这类网络的新型拉格朗日形式使得我们能够设计出功能强大的分布式模型，从而学习有用的表示，并为新架构的设计提供启发。本教程以现代术语和方法为核心，提供了对联想记忆的通俗入门，辅以实用的数学推导和代码笔记本，以促进实践操作与深入理解。

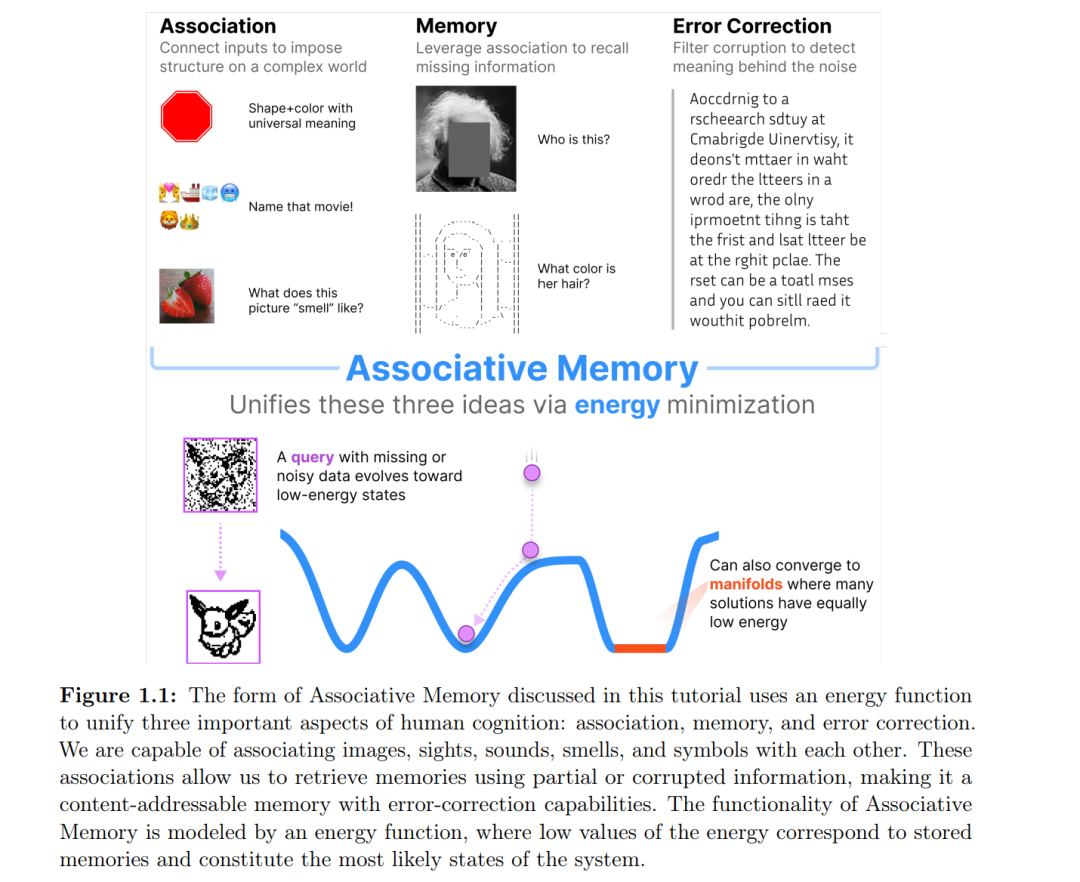
联想记忆（Associative Memory, AM）是心理学中的一个核心概念，负责将相关事物联系在一起 [1]。例如，当我们看到一张草莓的图片时，往往能回忆起这种水果的气味和味道；又比如看到一个人的照片，熟人通常能叫出其名字。图（1.1）中演示了 AM 的这一能力。这些都是记忆中被联想在一起的输入-输出对，其中给定对中的某个元素作为提示，可以通过内容寻址（content-addressable）的方式检索出另一个元素。 联想记忆的另一个重要方面是其纠错能力。如图（1.1）所示，尽管段落中的几乎所有单词都不是规范的英文单词，你仍能轻松阅读其中的文字。这是因为我们大脑中有强大的纠错机制，能够将不完美的输入与单词的正确语义进行关联。同样地，前面提到的草莓图片即便带有各种失真和缺陷，联想记忆仍能将其与正确的味道和气味相连接。 因此，联想记忆是一种具备纠错能力的、基于内容寻址的信息存储系统。 联想记忆在人工智能的发展历史中发挥了重要作用。在 1943 年，McCulloch 与 Pitts 提出了人工神经元模型 [2]；随后在 1950-60 年代，Frank Rosenblatt 开展了关于人工神经网络（ANN）——感知机（Perceptron）的大量研究 [3]。彼时，公众对未来充满热情，媒体宣称感知机会“行走、说话、看、写、自我复制，甚至意识到自身存在”[4]——类似于今日对 AI 的媒体报道。然而，在 1969 年，Minsky 和 Papert 证明简单的感知机（无隐藏层）甚至无法实现最基本的逻辑门，如 XOR [5]。这一结果严重打击了人们对神经网络的信心，导致研究热情骤降，多数计算机科学家离开了该领域，史学界称之为“AI 寒冬”[6]。 1982 年，John Hopfield 发表了开创性的论文 [7]，提出了如今被称为 Hopfield 网络的联想记忆模型，成为终结“AI 寒冬”的关键力量。Hopfield 将联想记忆的计算属性与凝聚态物理中 Ising 磁体 [8] 的集体现象联系起来。具体而言，Hopfield 提出了一个可量化的问题：对于一个由 D 个神经元组成的网络，它最多能存储和检索多少信息（即记忆）？内容寻址的联想记忆检索问题在当时具有足够的复杂性，可以展示神经网络的计算能力，同时又足够简单，便于利用统计物理中的强大工具进行解析求解。这种理论和工具的融合构建出神经网络计算的“简谐振子”级别抽象基础，为后续的扩展与推广奠定了坚实基础。 联想记忆曾是 1960 至 1980 年代神经网络研究的重要主题。虽然不完整但具有代表性的早期工作包括：Anderson [9]，Willshow、Buneman、Longuet-Higgins [10]，Amari [11; 12]，Cohen 与 Grossberg [13]，Hopfield [14]，Amit、Gutfreund、Sompolinsky [15] 等。 本教程的主要关注点是基于能量的联想记忆（Energy-based Associative Memories）。这类神经网络属于递归神经网络，可用状态向量表示，该向量随时间演化，遵循某种非线性规则。状态向量可以是连续的，也可以是离散的；更新规则可基于连续时间（微分方程），也可以是离散的更新步骤（通常视为微分方程的离散化）。状态更新方式也有多种：最常见的是同步更新（状态向量中所有元素同时更新）与异步更新（任一时刻仅更新一部分元素，例如随机选择一个元素更新，其余保持不变）。在本教程中，我们主要采用连续状态、连续时间以及同步更新的设定。 因此，网络的状态向量 x∈RDx \in \mathbb{R}^Dx∈RD，其分量记作 xix_ixi（索引 iii 从 1 到 DDD），满足如下微分方程：dxidt=fi(x,t)(1.1)\frac{dx_i}{dt} = f_i(x, t) \tag{1.1}dtdxi=fi(x,t)(1.1) 其中函数 fi(x,t)f_i(x, t)fi(x,t) 描述了系统的动力学向量场。我们将这些向量的分量称作“神经元”，尽管在某些情境下它们可能代表不同的生物结构，如星形胶质细胞或其分支。 一般的非线性耦合微分方程系统可能表现出复杂行为：如固定点、极限环、奇异吸引子或混沌行为。基于能量的联想记忆系统是这些系统的一个特殊子类，具有所谓的能量函数（有时称为李雅普诺夫函数）。可以将状态向量的时间演化类比为一个小球在复杂能量地形中“滚动下坡”，如图（1.1）所示。能量从下界有限，小球只能沿着能量减少的方向移动。由于这种限制，最终小球会停在某个局部极小值点，或到达一个能量平坦的流形上继续运动（只要能量不增加）。 这些局部极小值（可以是点吸引子——零维流形，也可以是高维流形）即为记忆。能量地形的塑造过程对应于信息写入网络，即学习；而沿能量下降轨迹的动力学过程则对应于记忆检索或推理。联想发生在网络的初始状态 x(t=0)x(t = 0)x(t=0) 与其最终状态 x(t→∞)x(t \to \infty)x(t→∞) 之间。最终状态通常是稳定的（除非位于能量平坦区域）。直观上讲，如果对状态的扰动未将其推离某个吸引子的“吸引盆地”，网络会自动进行纠正。因此该网络属于 AM 系统。 在某些设定下，记忆可能对应于训练数据中的具体样本；而在另一些情况下，它们可能是由学习算法（如反向传播 [16; 17]、Hebbian 学习 [18]、对比训练 [19; 20] 等）塑造出的吸引流形。在后者中，记忆通常不再代表某个具体样本，而是网络通过联想记忆结构、学习算法与训练数据之间的协同所获得的“知识”。 直观上，你可以将初始状态 x(t=0)x(t = 0)x(t=0) 理解为向神经网络提出的“问题”，它将状态向量定位在能量地形的某个高能区域。网络通过“下坡”寻求局部最小值——这就是“思考”的过程。一旦达到局部最小值，计算就终止，状态不再随时间演化。最终的状态 x(t→∞)x(t \to \infty)x(t→∞) 可作为回答读出。重要的是，这种计算方式不同于传统的前馈网络（如卷积网络、Transformer 或无思维链的 LLM 等）。传统网络的计算图是固定步数的，例如 10 层网络无论问题复杂与否都在第 10 层输出。而联想记忆网络的计算图是动态可适应的。简单问题可能在 5 步内得到答案，复杂问题可能需要更长时间“思考”。 此外，由于网络基于能量结构，其输出具有渐近稳定性。即一旦网络收敛到某个解，读取输出的时刻就不再重要。只要读取时刻 TTT 足够大，读取 x(t=T)x(t = T)x(t=T) 与 x(t=T+0.5秒)x(t = T + 0.5 \text{秒})x(t=T+0.5秒) 都将得到相同答案。这一性质使得联想记忆框架非常适合神经形态计算设备，即使硬件无法精确同步读取时间也能获得稳定输出。 近年来，联想记忆领域取得了重要进展，尤其是稠密联想记忆（Dense Associative Memories, DenseAMs） 的发展 [21]。这是一类灵活的、基于能量的 AM 架构，具备强大的信息存储能力，能够在结构中融入多种有用的归纳偏置（如卷积 [22]、注意力机制 [23] 等），并具备对新出现的局部极小值的可控性。DenseAM 的思想引发了关于 AM 潜在应用的大量创新思考，我们相信它将开启 AM 研究的新前沿 [24]。 本教程将从理论和实践两个层面介绍上述新发展。教程配有代码笔记本与习题，鼓励读者动手实现 AM 网络，应用于自己的任务。我们刻意将问题设计得简洁但具启发性，以便读者掌握 AM 中的数学思想与核心概念。希望你能享受这段学习之旅。