大模型推理的天花板在哪里？

摘要

近期新一代前沿语言模型引入了大型推理模型（Large Reasoning Models，LRMs），这些模型在给出最终答案之前，会先生成详尽的思考过程。尽管它们在各类推理基准上的表现显著提升，其基本能力、规模化特性及内在局限性仍未得到充分理解。目前的评估主要聚焦于既有的数学和编码基准，强调最终答案的准确率；然而，这种评估范式往往受到数据污染的影响，且无法深入剖析推理痕迹（reasoning traces）的结构与质量。在此背景下，本文借助可控谜题环境，系统地填补这些认知空白：该环境既可精确操控组合复杂度，又保持逻辑结构一致，不仅可以评估最终答案，也能追踪并分析模型内部的推理轨迹，以洞见LRMs的“思考”方式。通过对多种谜题任务进行大规模实验证明，当前前沿LRMs在超过某一复杂度阈值后会出现准确率的完全崩溃；更令人意外的是，它们的推理努力随着问题复杂度上升而增加，但在达到临界点后即便拥有充足的推理token预算也会骤然下降，展现出一种反直觉的规模化极限。我们还将LRMs与标准大型语言模型（LLMs）在相同推理计算预算下进行对比，识别出三种性能区间：（1）在低复杂度任务上，标准模型反而意外地优于LRMs；（2）在中等复杂度任务上，LRMs因额外的思考环节而表现出优势；（3）在高复杂度任务上，二者皆陷入完全崩溃。此外，我们发现LRMs在精确计算方面存在明显局限：它们无法可靠地执行显式算法，在不同谜题任务中的推理表现也极不一致。进一步深入分析推理痕迹时，我们研究了模型探索解空间的模式并剖析了其计算行为，揭示了LRMs的优势与短板，并最终对其真正的推理能力提出了关键质疑。

关键词：Large Reasoning Models (LRMs)、问题复杂度 ，可控谜题环境 (controllable puzzle environments)、思维痕迹 (reasoning traces)、过度思考 (overthinking)、推理计算预算 (inference compute budget)********************************

集智编辑部丨作者

论文题目：The Illusion of Thinking: Understanding the Strengths and Limitations of Reasoning Models via the Lens of Problem Complexity 发表时间：2024年10月22日 论文地址：https://ml-site.cdn-apple.com/papers/the-illusion-of-thinking.pdf **

**

近年来，随着大型语言模型（LLMs）的飞速发展，一类专门针对推理任务进行优化的“大型推理模型”（Large Reasoning Models, LRMs）应运而生。与传统仅输出答案的LLM不同，LRM通过“链式思维”（chain‐of‐thought, CoT）或自我反思机制，先生成详尽的思考过程再给出答案。尽管在诸多数学与编码基准上表现优异，其真正的推理能力、规模化性能及内在局限尚未得到系统评估。近期苹果公司发表论文，借助可控谜题环境（经典Tower of Hanoi、Checkers Jumping、River Crossing、Blocks World等），深入剖析LRM在不同复杂度下的表现，并揭示其“推理崩溃”与“过度思考”现象。

LRM的崛起与研究动机

随着OpenAI o1/o3、Anthropic Claude 3.7 Sonnet Thinking、Google Gemini Thinking等LRM的横空出世，研究者纷纷将其视作通向更通用人工智能的关键一步。早期LLM在推理基准上表现不佳，研究者尝试通过规模化训练数据及推理时计算（inference compute budget）来提升性能。思维链（CoT）与自我校验（self‐verification）策略，虽能在一定程度上提高准确率，却带来了所谓的“过度思考”（overthinking）——在找到正确思路后仍持续无效探索，浪费推理预算。

在模型的评估测试方面，大多只是聚焦于推理模型最终给出答案的准确率。此外，测试所使用的大量经典数学基准，如MATH-500、AIME系列常存在样本泄露或缺乏复杂度可控性等问题，难以分辨模型是凭借记忆还是算法推理。因此，本研究在此基础上，构建可精细控制复杂度且规则明晰的测试环境，同时检验模型的答案与思维痕迹，并通过模拟器精确核验中间解与最终结果，从而揭示LRM的真正“思考”面貌。

可控谜题环境的设计与优势

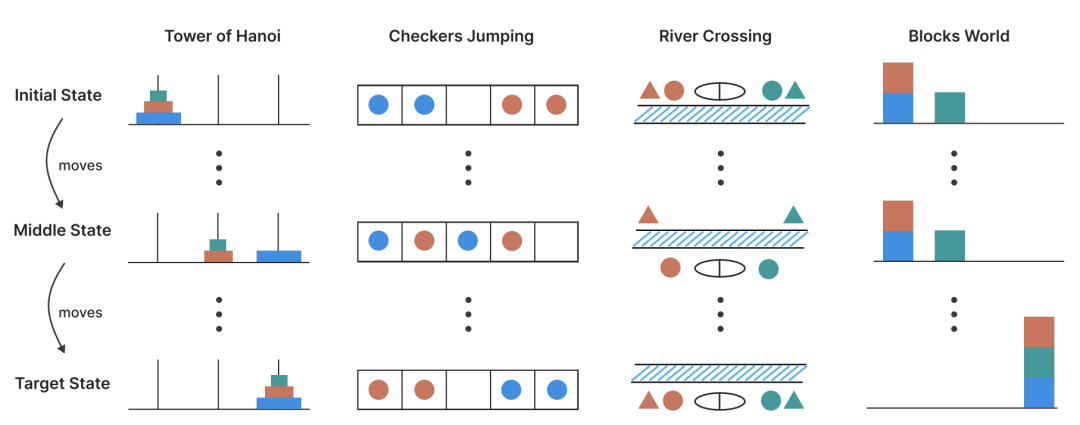
为了系统操控问题复杂度并保持逻辑结构一致，研究团队选取了四类经典谜题： * 河内塔（Tower of Hanoi）：通过盘子数量控制组合深度，考察模型的递归规划与状态管理能力； * 跳棋谜题（Checkers Jumping）：在线性布局中交换红蓝棋子位置，检测模型对局面转换规则的理解与前瞻能力； * 过河问题（River Crossing）：多对“执行者—保护者”在约束条件下渡河，评估多主体协调与约束管理； * 积木世界（Blocks World）：在堆栈间转换块状物，考验模型对依赖关系和临时重组的规划思路。

这四种环境均配备专门模拟器，实现对每一步移动合法性与最终目标状态的精确校验，为深入分析LRM“思维”提供了可靠工具。

图 1. 四种谜题环境的图解。每一列展示了谜题从初始状态（上）到中间状态（中）再到目标状态（下）的过程：河内塔（通过木桩运输圆盘）、跳棋（交换两种颜色标记的位置）、渡河（将个体运送过河）和方块世界（堆栈重新配置）。

实验设计与方法

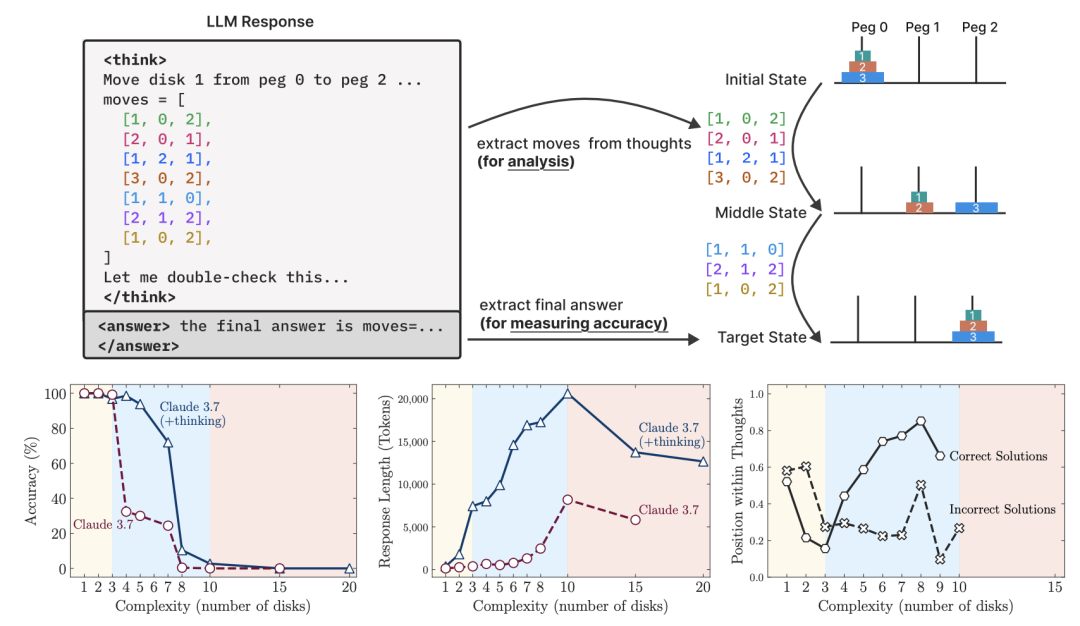
研究以Claude 3.7 Sonnet（thinking/no‐thinking）和DeepSeekR1/V3为代表，允许最大64k推理token预算。对每种谜题、每个复杂度N，均生成25个实例并取平均性能。实验主要衡量： * 答案准确率：模型最终是否正确完成谜题； * 推理token使用量（thinking tokens）：LRM在思维过程阶段消耗的计算预算； * 中间解探索轨迹（reasoning traces）**：**利用模拟器提取并标记思考中的每个候选解，分析其先后顺序及正确性。

图 2. 上图：我们的设置可以验证最终答案和中间推理痕迹，允许对模型思维行为进行详细分析。左下和中下：在低复杂度下，非思考模型更准确，效率更高。随着复杂性的增加，推理模型的表现会更好，但需要更多的tokens——直到它们都超过了一个临界阈值，并且跟踪时间更短。右下：对于正确解决的案例，Claude 3.7 Thinking倾向于在低复杂性的情况下早期找到答案，在高复杂性的情况下后期找到答案。在失败的情况下，它通常会关注早期的错误答案，浪费剩余的tokens预算。这两种情况都揭示了推理过程的低效。

**

**

**

**

复杂度对推理行为的影响：三大阶段

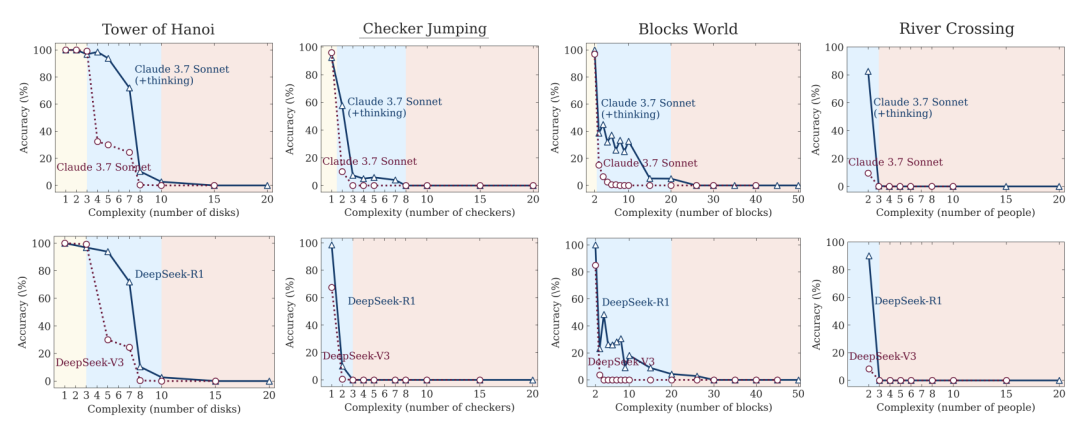
实验结果显示，随着问题复杂度的增加，LRM与非思维LLM在谜题环境中呈现三个显著推理阶段： 1. 低复杂度阶段：标准LLM表现出色，推理更高效、准确率甚至超过LRM； 1. 中等复杂度阶段：引入思维痕迹后，LRM开始在准确率上领先，但其推理token消耗也显著攀升； 1. 高复杂度阶段：无论思维与否，所有模型准确率均骤降，出现“推理崩溃”现象——无法给出任何有效解答。

在高复杂度区域，发现LRM的推理token反而出现下降趋势——尽管仍有充足预算，模型却减少思考长度并放弃探索，导致完全失败；这一“计算规模极限”暗示了模型在面对更深组合链条时的固有障碍。此外，即便在中等复杂度，LRM也常在找到正确解后继续无谓探索，不仅拖慢推理速度，更加重了计算负担，印证了文献中所称的“过度思考”（overthinking）。

图 3. 思维模型（Claude 3.7 Sonnet with thinking, DeepSeek-R1）与非思维模型（Claude 3.7 Sonnet, DeepSeek-V3）在所有谜题环境和不同问题复杂程度中的准确性。

**

**

深入分析思考痕迹：探索与自我校正能力

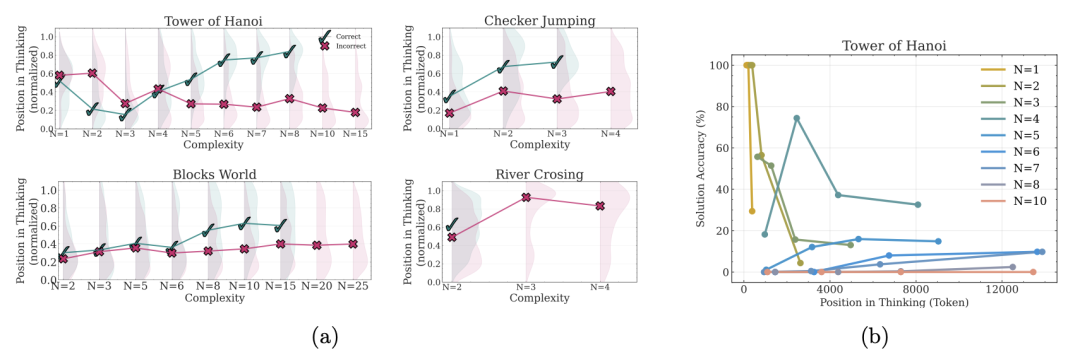
借助模拟器提取每条思考痕迹中的中间解，本研究将正确与错误解在思维过程中的出现位置进行定量对比。结果显示： * 在简单问题中，正确解往往较早出现，但随后的错误解涌现，分布向思维后段倾斜； * 在中等复杂度中，模型初期多探索错误路径，只有在后期才汇聚到正确解； * 在复杂度阈值以上，思路全线崩溃，思考痕迹中再无任何正确片段。

这一行为模式揭示了LRM有限的自我校正能力：虽然具备一定纠错潜力，却因效率低下或计算预算管理失衡，难以持续收敛至解。

图 4. 左和中：在四个不同复杂程度的谜题的推理轨迹中，中间解决方案的位置和正确性。✓表示正确的解决方案；x 表示不正确的解决方案，用阴影表示分布密度；右图：河内塔在不同复杂程度下的解决方案准确性与思考位置。简单问题（N=1-3）表现出早期的准确性随着时间的推移而下降（过度思考），中等问题（N=4-7）表现出持续推理的准确性略有提高，复杂问题（N≥8）表现出持续接近零的准确性，表明完全推理失败。

意外发现与未解之谜

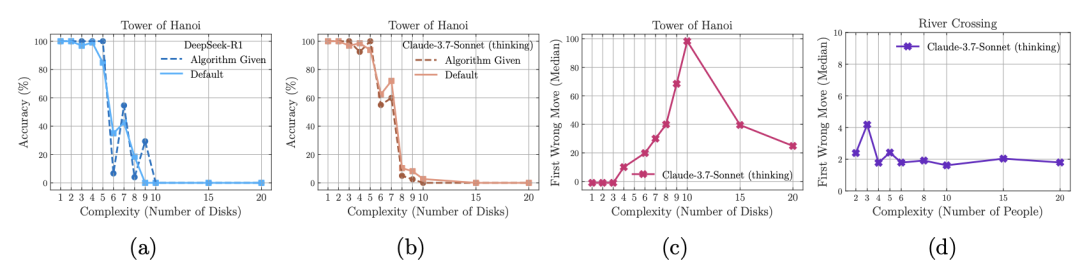
为验证模型的符号执行能力，研究团队在提示中直接提供了河内塔（Tower of Hanoi）的解决算法，结果却未见性能提升，崩溃阈值与默认场景基本一致，凸显LRM在精确执行给定逻辑步骤时的局限。此外，不同谜题环境中，模型的首个错误移动所处位置相差甚远：在河内塔中可保持数百步无失误，而在过河问题（River Crossing）中第一错仅出现在第四步，或许与训练数据中例子稀缺度有关，提示LRM仍在一定程度上依赖记忆而非纯粹算法推理。

图 5. (a)和(b)尽管在提示符中提供了求解算法，但执行失败发生在相似的点，突出了逻辑步骤执行中的推理模型局限性。(c)和(d)值得注意的是，Claude 3.7 Sonnet模型在河内塔的无错误序列比在过河情景中的早期错误长得多。

结论、展望与思考

通过可控谜题环境的系统评估，研究首次揭示了当前LRM在问题复杂度维度上的三大推理阶段与计算规模极限，深入剖析了“过度思考”与自我校正的不稳定性，并通过思考痕迹量化了模型的探索策略。研究挑战了对LRM推理能力的诸多假设，表明其在泛化与符号操作上仍面临重大瓶颈。

尽管谜题环境提供了优越的复杂度可控性与精确验证，但毕竟狭窄地聚焦于结构化规划问题，难以全面代表真实世界中知识密集型与开放式推理场景。此外，实验依赖闭源API，限制了对模型内部架构与权重的深入剖析。最后，模拟器的精确性在高度非结构化领域或难以复制，提示未来需拓展至自然语言理解、常识推理等更富挑战性的任务域。