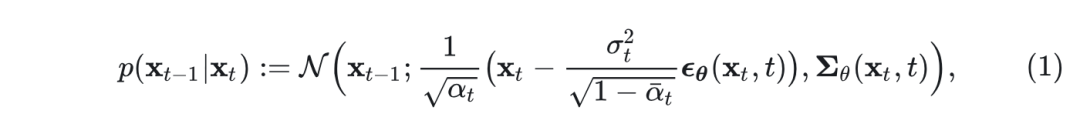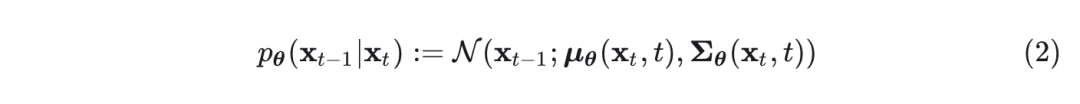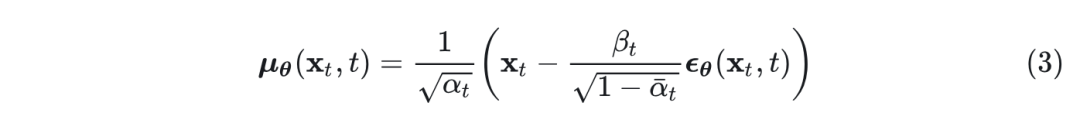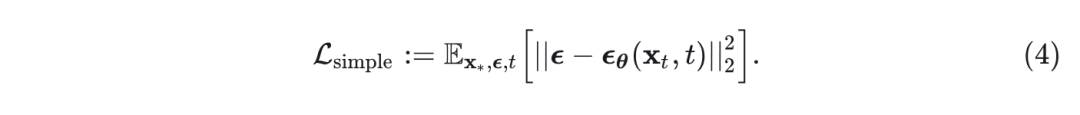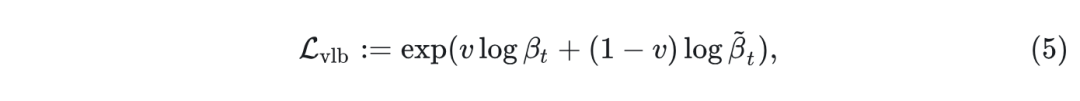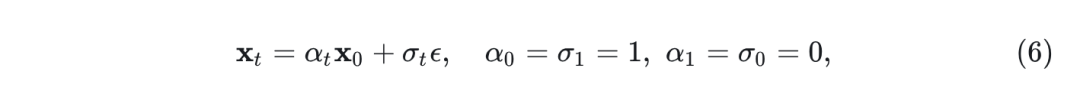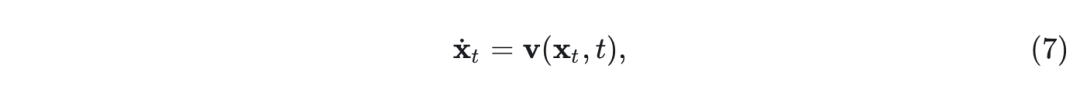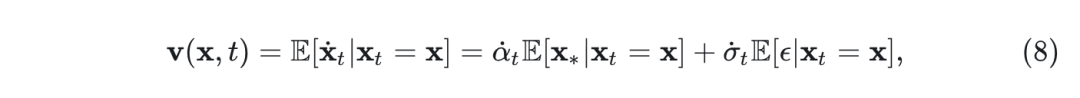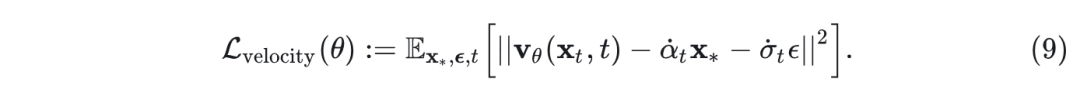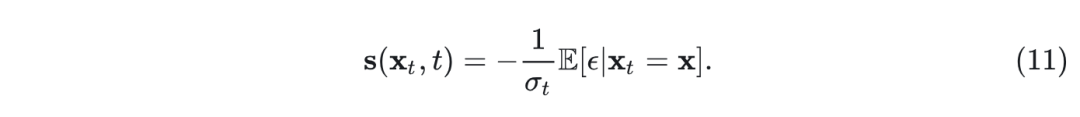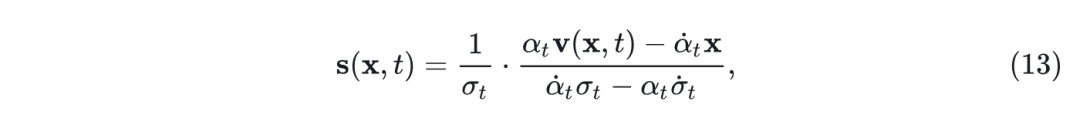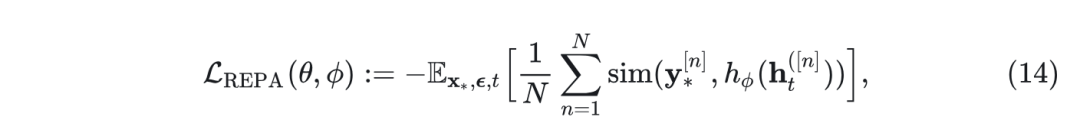作者丨科技猛兽编辑丨极市平台
极市导读 表征的对齐真的很重要!之前我们训练扩散模型的路可能是错误的。
本文目录
1 Representation Alignment:扩散模型与自监督方法的表征 "对齐"
(来自 KAIST,Korea University,Scaled Foundations,New York University) 1 REPA 论文解读 1.1 REPA 研究背景 1.2 DDPM 和 Flow-based Model 简介 1.3 本文观点总结 1.4 REPA 的三点观察
太长不看版
训练扩散模型可能比你想象的更简单。
纽约大学谢赛宁老师团队最近的工作提出: 当我们训练扩散模型时,把扩散模型与自监督方法的表征"对齐" (Representation Alignment) ,使得扩散模型的训练比你想象的还简单。 因为最近有些研究表明:扩散模型中包含的 (生成式) 去噪过程,可以诱导得到一些 (判别式) 的特征。虽然这些判别式的表征的质量落后于自监督学习 (DINO v2) 得到的表征。

- 扩散模型能够给出一些合理的表征,越好的扩散模型的 Representation 越强。
- 即便如此,这些 Representation 与自监督方法得到的视觉架构 (如 DINOv2, MAE) 的 Representation 相比还有所不足。
- 当把扩散模型和 DINOv2 的表征对齐时,扩散模型在训练时可以稳步提升。
图3:一些观察 (图源谢赛宁老师 Twitter) 这个方法带来的效益是: 训练主流扩散模型 DiTs 和 SiTs 变得明显容易,在训练效率和生成质量方面都有显著的改进:ImageNet 256×256 实现了最先进的 FID=1.42。将 SiT 训练速度提高了 17.5 倍以上,本方法 400K 步训练的模型与常规条件下训练了 7M 步的 SiT-XL 模型的性能匹配。此外,这种方法还具有良好的扩展性,即对于更大的模型,改进幅度更大。 下面是对本文的详细介绍。
1 Representation Alignment:扩散模型与自监督方法的表征 "对齐"
论文名称:Representation Alignment for Generation: Training Diffusion Transformers Is Easier Than You Think
论文地址:
http://arxiv.org/pdf/2410.06940 代码链接:
http://github.com/sihyun-yu/REPA 项目主页:
1.1 REPA 研究背景
基于去噪的生成模型,例如 Diffusion Model[1][2]和 Flow-based Model[3][4]已成为生成高维视觉数据的可扩展方法。这些模型在文生图 (SDXL, SD3) 等有挑战性的任务中取得了不错的结果。 最近的工作探索了使用扩散模型做表征学习,比如[5][6]和恺明的 l-DAE[7],并表明扩散模型的 hidden state 可以学习到判别式的表征,而且更好的扩散模型往往可以学习到更好的表征。
1.2 DDPM 和 Flow-based Model 简介
Diffusion Model
Diffusion Model 通过学习从高斯分布 到 的逐渐去噪过程来建模目标分布 。在形式上, 扩散模型的正向过程 : 从 开始, 对于 , 逐渐添加高斯噪声。扩散模型学习反向过程 。 对于给定的 可以被建模为 。其中 是预定义超参数。DDPM 表明,如果反向过程 ( , for 表示为:
在 DDPM 中,。 即:
其中,均值满足:
其中,可以使用由简单去噪自编码器目标进行训练:
IDDPM[8]进一步展示出如果模型通过下面的目标函数同步学习,则可以进一步提高性能:
其中, 表示每个维度的变量, 且有 。 在足够大的 和合适的 的调度下, 分布 几乎变成各向同性高斯分布。因此, 可以从随机噪声开始生成样本并执行迭代反向过程 来获得数据样本 。
Flow-based Model
Flow-based Model 处理连续时间相关过程 , 使用数据 和高斯噪声
其中, 和 分别为 的递减和递增函数。存在一个速度场的概率流常微分方程 (Probability Flow Ordinary Differential Equation, PF ODE):
其中这个 ODE 在 处的分布等于边际 。 速度 表示为两个条件期望的总和:
通过最小化以下训练目标,可以用模型 近似:
注意这也对应于以下反向随机微分方程 (Stochastic Differential Equation, SDE):
其中 score类似地变为条件期望:
与 类似, 可以用模型 近似, 目标如下:
这里, score 可以使用 的速度 直接计算为:
因此,只估计两个向量中的一个就足够了。 随机插值 (Stochastic interpolants) 显示任何 和 都满足 3 个条件: 1.
- and are differentiable,
导致在 和 之间进行插值而不产生偏差的过程。因此,可以通过在训练和推理期间将它们定义为一个简单的函数来使用一个简单的插值,例如:
- 线性插值器: 。
- 方差保持 (Variance-Preserving, VP) 插值器: 。
随机插值的另一个优点是扩散系数 在训练任何分数或速度模型时是独立的。因此, 当使用反向 SDE 进行采样时, 也可以在训练后明确选择 。 注意现有的基于分数的扩散模型,包括 DDPM,同样可以解释为 SDE。它们的前向扩散过程可以解释为预定义的 离散化的前向 SDE, 其平衡分布为 , 其中训练是在 上进行的 ( 足够大比如为 1000), 其中 几乎为各向同性高斯分布。生成是通过假设 , 并从随机高斯噪声开始求解相应的反向 SDE 来完成的, 其中 和扩散系数 是从前向扩散过程中隐式选择的, 这可能导致 Score-based Diffusion Model 的设计空间过于复杂。
1.3 本文观点总结
本文观点是:训练扩散模型的主要挑战和主要瓶颈是需要学习高质量的内部表征h。
本文证明了:在生成式扩散模型的训练过程中,当有外部表征支持时,训练会变得更加简单,更加有效。
本文贡献是:提出了一种简单的正则化技术,该技术利用自监督视觉表征,提高了训练效率和扩散模型的生成质量。
本文的探索过程: 发现预训练的扩散模型的确会学习到有意义的判别式表征 → 但是,这些表征明显不如 Dinov2 的表征 → 发现扩散模型学习的表征与 DINOv2 的表征之间的对齐仍然很弱(相比于 Dinov2 与自监督模型比如 MoCov3 这种表征之间的对齐) → 观察到扩散模型和 Dinov2 之间的对齐,随训练更长和模型更大而不断提高
这些发现启发本文通过结合外部自监督模型的表征来增强生成式扩散模型。 然而,使用现成的自监督视觉编码器 (比如通过对生成任务的编码器进行微调) 时,这种方法并不直接。
- 挑战1: 输入不匹配,扩散模型的输入是有噪声的,而大多数自监督学习编码器都是在干净的图像上训练的。
- 挑战2: 这些现成的视觉编码器不是为重建或生成等任务设计的。
为了克服这些技术问题,本文使用一种正则项技术表征对齐 (REPresentation Alignment, REPA) 来指导扩散模型的表征学习,将预训练的自监督表征蒸馏到扩散模型的表征中。 本质上, REPA 将干净图像 的预训练自监督视觉表征 蒸馏为噪声输入 的扩散模型的表征 。这种正则化减少了表征 中的语义差距,并更好地将其与目标自监督视觉表征 对齐。这种增强的对齐显着提高了扩散 Transformer 的生成性能。有趣的是, 对于 REPA, 作者观察到仅通过对齐前几个 Transformer Block 就可以实现足够的表征对齐。反过来, 这允许 Diffusion Transformer的后续层专注于基于对齐的表征来捕获高频细节,以进一步提高生成性能。
1.4 REPA 的三点观察
假设扩散模型为 , 其中 是 latent 变量, 满足 。作者把扩散模型 视为 2 个函数的组合: 。其中 Encoder 是 , Decoder 是 。其中编码器 隐式地学习 , 来重建 。 作者首先研究了 ImageNet 上预训练的 SiT[10]模型的逐层行为,该模型使用线性插值和速度预测进行训练。作者专注于测量 Diffusion Transformer 与最先进的自监督 DINOv2[11]模型之间的表征的差距。 作者从 3 个角度检查这一点:语义差距、特征对齐进展及其最终特征对齐。 对于语义差距,作者使用 DINOv2 特征与为 7M training iterations 训练的 SiT 模型的 linear probing 的结果进行比较。 对于特征对齐,作者使用 CKNNA[12],这是一种与 CKA 相关的内核对齐度量,但基于相互最近邻。这允许定量评估不同表示之间的对齐。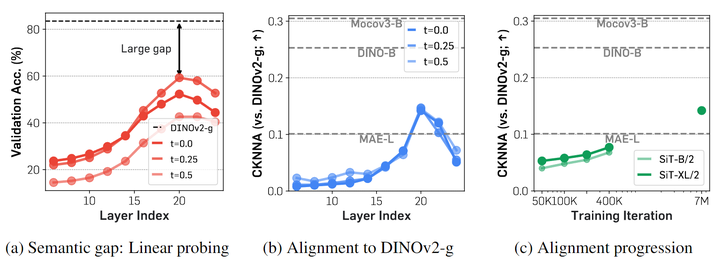
观察1:Diffusion Transformer 与最先进的 Visual Encoder 表现出显著的语义差距。
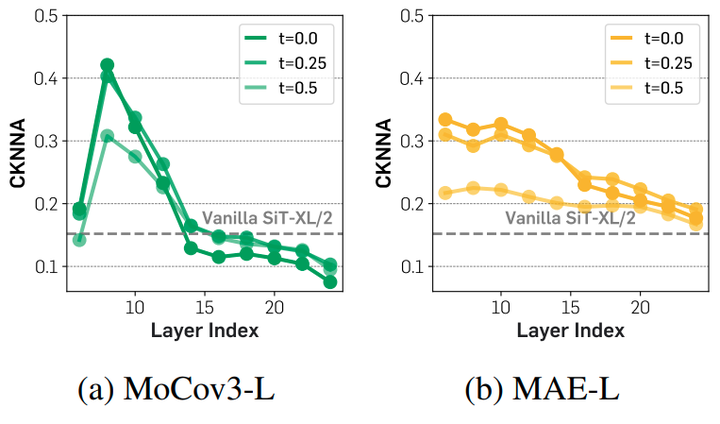
如图 4(a) 所示,与之前的工作[6][7]一致,作者观察到预训练的 Diffusion Transformer 的隐藏状态表征在第 20 层实现了相当高的 Linear Probing 峰值。然而,它的性能仍然远低于 DINOv2,这表明两种表征之间存在实质性的语义差距。此外,本文发现,在达到峰值后,Linear Probing 性能迅速下降,这表明 Diffusion Transformer 必须摆脱只关注学习语义丰富的表征,以生成高频细节的图像。
观察2:扩散表征与其他视觉表示已经较弱地完成对齐。
在图 4(b) 中,作者使用 CKNNA 报告了 SiT 和 DINOv2 之间的表征对齐。SiT 模型表示已经显示出比 MAE 更好的对齐。然而,绝对的对齐分数仍然低于在其他自监督学习方法 (例如 MoCov3 与 DINOv2)之间观察到的分数。这些结果表明,虽然 Diffusion Transformer 的表征表现出与自监督视觉表示的一些对齐,但对齐仍然很弱。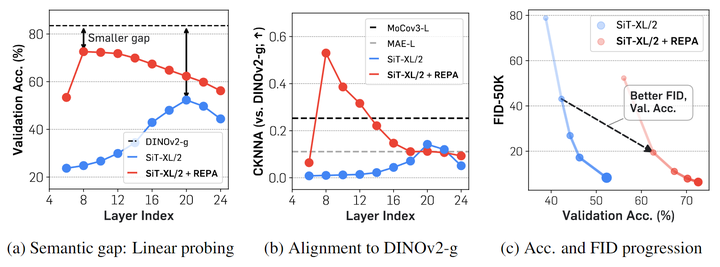
观察3:随着模型规模扩大,训练更多,对齐也会更好。
作者还测量了不同模型大小和训练迭代的 CKNNA 值。如图 4(c) 所示,作者观察到与模型更大,训练更长可以改进对齐水平。然而,绝对的对齐数值仍然很低,并且没有达到其他自监督视觉编码器 (例如 MoCov3 和 DINOv2) 的水平。 这些发现不是只对 SiT 模型有效,也对其他的扩散模型有用。比如作者也在 ImageNet 上预训练的 DiT 模型进行了类似的分析,也在图 4 中观察到了类似的结论。
1.6 特征对齐
REPA 将模型隐藏状态的 Patch 投影与预训练的自监督视觉表征对齐。作者使用干净的图像表征作为目标,研究这个影响。这个正则项的目的是为了 Diffusion Transformer 的隐藏层从带噪声的图片中预测干净的视觉表征,这些表征包含有用的语义信息。这为后续层重建目标提供了有意义的指导。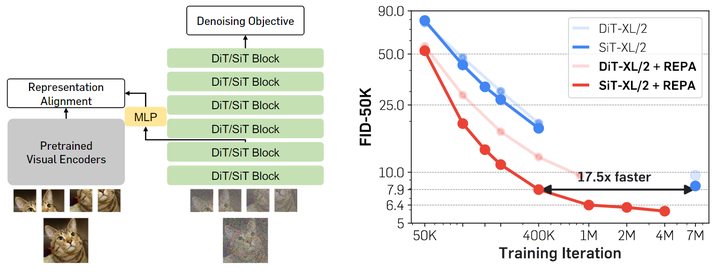
其中 是 Patch index, 是预定义的相似度函数。 把这一项添加到原来训练扩散模型的目标函数 中:
其中 是一个超参数, 用于控制去噪和表示对齐之间的权衡。作者主要研究这个正则项 对两个流行目标的影响, 即:DiT 中使用的改进 DDPM 和 SiT 中使用的线性随机插值。
1.7 实验设置
在实验部分作者探究了下面 3 个问题:
- REPA 能否显着改善 Diffusion Transformer 的训练。
- REPA 在模型大小和表征的质量方面是否具有可扩展性。
- Diffusion Model 表示是否可以与各种视觉表征对齐?
作者严格遵循 DiT 和 SiT 的实验设置,使用 Stable Diffusion VAE 将每张图像编码为压缩向量 。对于模型配置,使用 DiT 和 SiT 论文中引入的 B/2、L/2 和 XL/2 架构,该架构处理 Patch Size 为 2 的输入。为了确保与 DiTs 和 SiTs 进行公平比较,作者在训练期间始终使用 256 的 Batch Size。 评测指标: FID、sFID,IS、精度 (Pre.) 和召回率 (Rec.)。使用 50,000 个样本。还包括 Linear Probing 结果 (Acc.) 和 CKNNA。 采样器: 遵循 SiT 的作者使用 SDE Euler-Maruyama Sampler (对于 w_t = \sigma_tw_t = \sigma_t 的 SDE),默认情况下将函数评估 (NFE) 的数量设置为 250。
基线模型 4 类:
- Pixel diffusion:ADM, VDM++, Simple diffusion, CDM
- Latent diffusion with U-Net: LDM
- Latent diffusion with transformer+U-Net hybrid models: U-ViT-H/2, DiffiT, 和 MDTv2-XL/2
- Latent diffusion with transformers: MaskDiT, SD-DiT, DiT, 和 SiT
如下图 7 所示,作者发现 REPA 在各种设计选择中始终可以显著提升生成性能,实现更好的 FID 分数。下面,我们对每个组件的影响进行了详细的分析。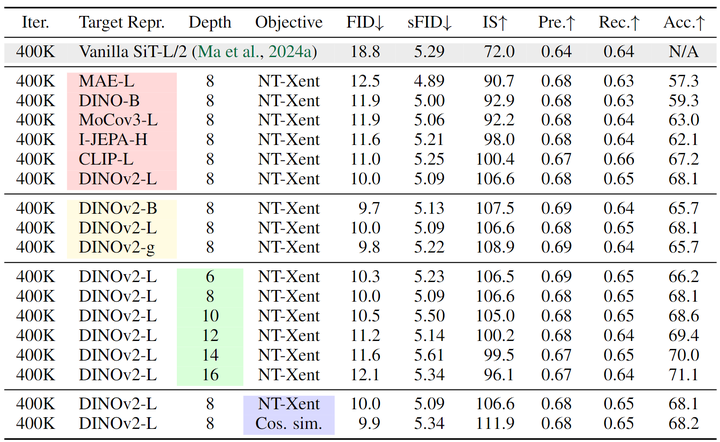
如图 7 所示,作者首先分析了使用不同的预训练的自监督编码器作为目标表征的对比。视觉编码器的质量与 Diffusion Transformer 的性能之间存在很强的相关性。如果视觉编码器的表征更有意义,扩散模型不仅捕获了更好的语义,而且表现出增强的生成性能。 视觉编码器尺寸
如图 7 所示,作者评估不同尺寸 DINOv2 模型 (DINOv2-B, L, g) 来研究编码器大小的影响。可以观察到,性能差异是微不足道的,作者假设这是由于所有 DINOv2 模型都是从 DINOv2-g 模型中提取的,因此共享相似的表征。 对齐深度
如图 7 所示,作者还研究了将 REPA 损失附加到不同层的效果,发现在训练中只正则化前几个层 (例如8) 就足够了。有趣的是,将正则化限制在前几层进一步提高了生成性能 (例如,将REPA添加到第 6 层或第 8 层会产生最好的结果)。作者假设这个原因是剩余的层能够在强大的表征之上。专注于捕获高频细节。 对齐目标函数
如图 7 所示,作者比较了 2 种简单的对齐训练目标:Normalized Temperature-scaled Cross Entropy (NT-Xent)[13]或负余弦相似度 (cos. sim.)。作者发现 NT-Xent 在早期阶段 (例如 50-100K iteration) 更有优势,但差距随着时间的推移而减少。因此在未来的实验中选择 cos. sim.。 最后,作者通过改变 Visual Encoder 和 Diffusion Transformer 的大小来研究 REPA 的可扩展性。如图 8(a) 所示,与更强的表征对齐可以提高生成结果和 Linear Probing 性能。此外,随着 Diffusion Transformer 尺寸的增加,REPA 的收敛速度更显著。作者通过绘制图 8(b) 中有和没有 REPA 的不同 SiT 模型的 FID-50K 来证明这一点:REPA 使用更大的模型更快地实现了相同的 FID。最后,图 8(c),保持 Visual Encoder 固定为 DINOv2-B,该图显示了随 Diffusion Transformer 尺寸的变化而变化 Linear Probing 结果和 FID 之间的关系。更大的模型随着训练时间更长,表现出更陡峭的性能改进 (生成和 Linear Probing 的增益更快)。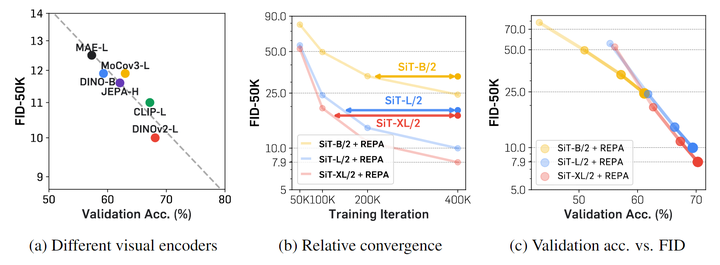
基于以上分析,作者对最先进的 Diffusion Model 和带有 REPA 的 Diffusion Transformer 进行了系统级的比较。首先比较了原始 DiT 或 SiT 模型与使用 REPA 训练的相同模型之间的 FID 值。如图 9 所示,REPA 在所有模型变体中显示出一致且显着的改进。特别是,在 SiT-XL/2 上,对齐表征只需训练 400k 步即可获得 FID=7.9,这已经在 超过了原始 SiT-XL 训练 7M 步的 FID。随着训练时间的延长,性能继续提高。使用 SiT-XL/2,FID 在 1M 步变为 6.4,在 4M 步变为 5.9。作者还在图 10 中定性地比较了生成结果,使用 REPA 训练的模型表现出更好的结果。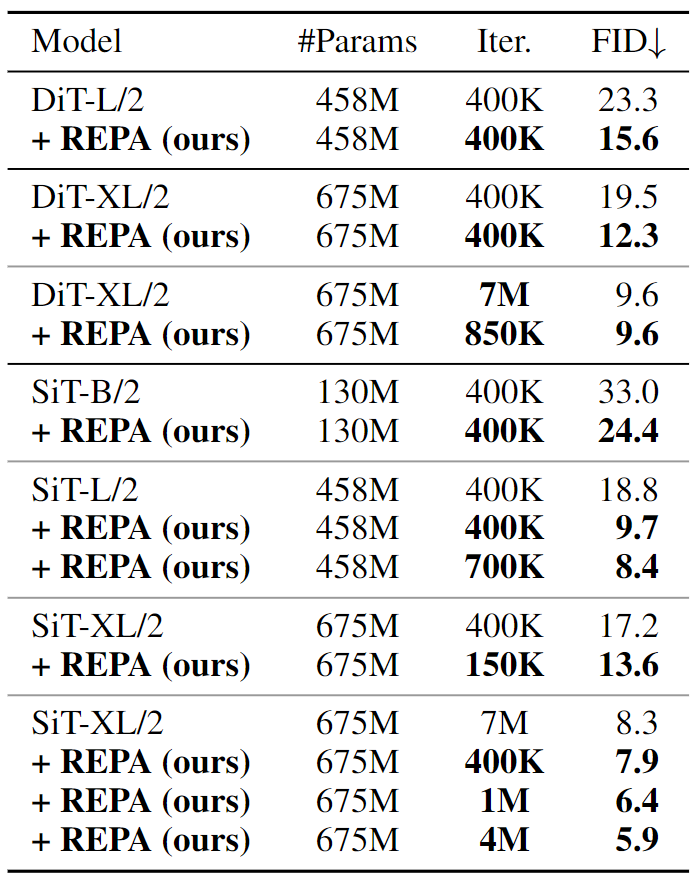



消融实验结果
不同 timestep 的表征
作者首先对比了不同 noise scale (即不同 timestep) 下的 SiT 模型输出的语义差异 (通过 Linear Probing 精度衡量),与干净的 DINOv2-g 表征之间的最大 CKNNA 值。结果如下图 13 所示,在不同的噪声水平下,REPA 始终可以缩小表征的差距,比如获得更好的 Linear Probing 结果和更高的 CKNNA 值。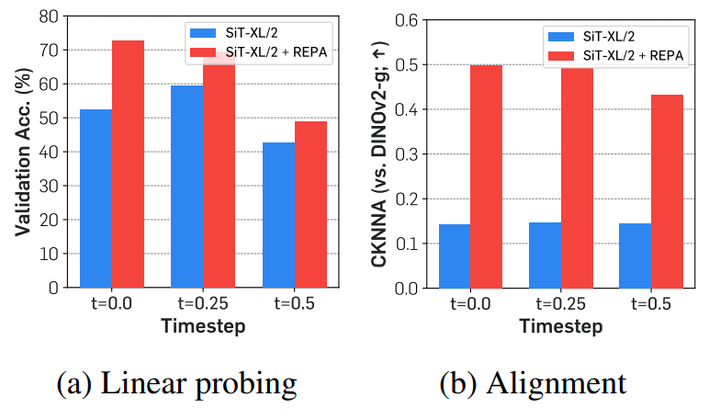
1.^abDenoising Diffusion Probabilistic Models 2.^Score-based generative modeling through stochastic differential equations 3.^Flow matching for generative modeling 4.^Flow straight and fast: Learning to generate and transfer data with rectified flow 5.^Your Diffusion Model is Secretly a Zero-Shot Classifier 6.^abDenoising Diffusion Autoencoders are Unified Self-supervised Learners 7.^abDeconstructing Denoising Diffusion Models for Self-Supervised Learning 8.^Improved denoising diffusion probabilistic models 9.^Flow matching for generative modeling 10.^SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers 11.^DINOv2: Learning Robust Visual Features without Supervision 12.^The platonic representation hypothesis 13.^A simple framework for contrastive learning of visual representations

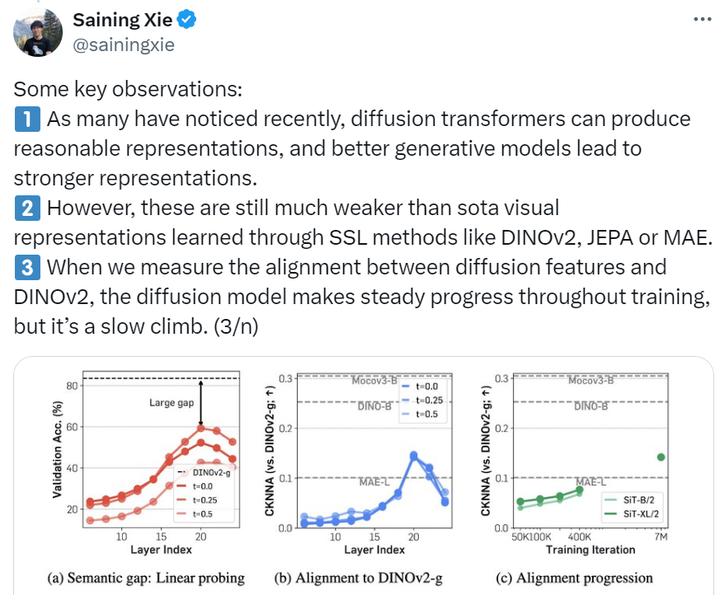 图3:一些观察 (图源谢赛宁老师 Twitter) 这个方法带来的效益是: 训练主流扩散模型 DiTs 和 SiTs 变得明显容易,在训练效率和生成质量方面都有显著的改进:ImageNet 256×256 实现了最先进的 FID=1.42。将 SiT 训练速度提高了 17.5 倍以上,本方法 400K 步训练的模型与常规条件下训练了 7M 步的 SiT-XL 模型的性能匹配。此外,这种方法还具有良好的扩展性,即对于更大的模型,改进幅度更大。 下面是对本文的详细介绍。
图3:一些观察 (图源谢赛宁老师 Twitter) 这个方法带来的效益是: 训练主流扩散模型 DiTs 和 SiTs 变得明显容易,在训练效率和生成质量方面都有显著的改进:ImageNet 256×256 实现了最先进的 FID=1.42。将 SiT 训练速度提高了 17.5 倍以上,本方法 400K 步训练的模型与常规条件下训练了 7M 步的 SiT-XL 模型的性能匹配。此外,这种方法还具有良好的扩展性,即对于更大的模型,改进幅度更大。 下面是对本文的详细介绍。