A high-precision framework for phase-field fracture interface reconstructions with application to Stokes fluid-filled fracture surrounded by an elastic medium

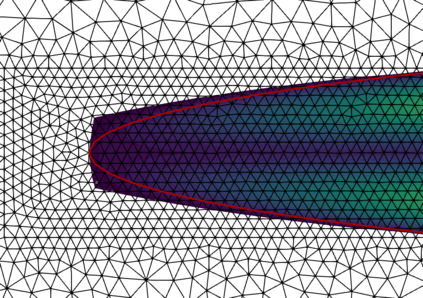
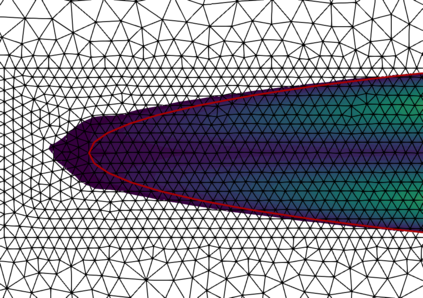
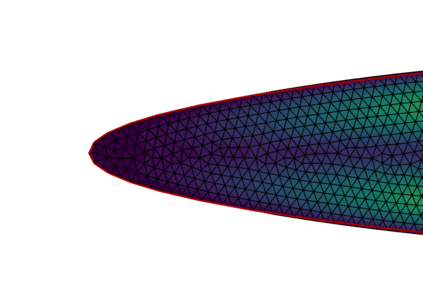
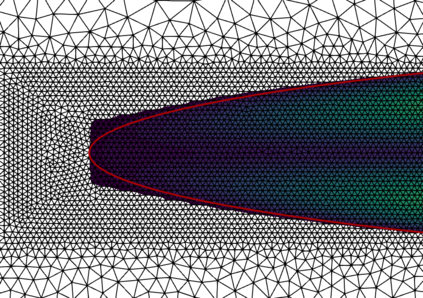
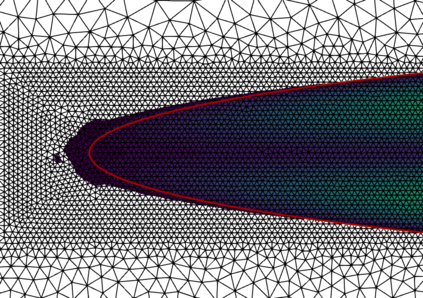
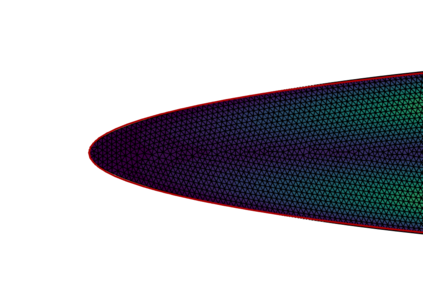
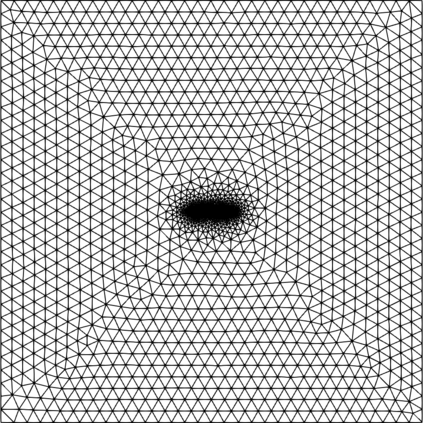
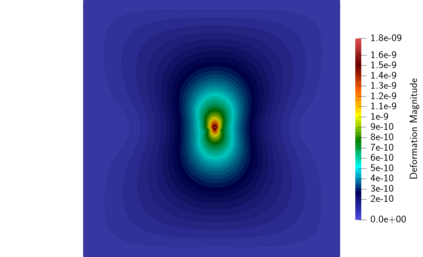
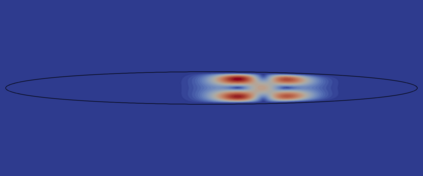
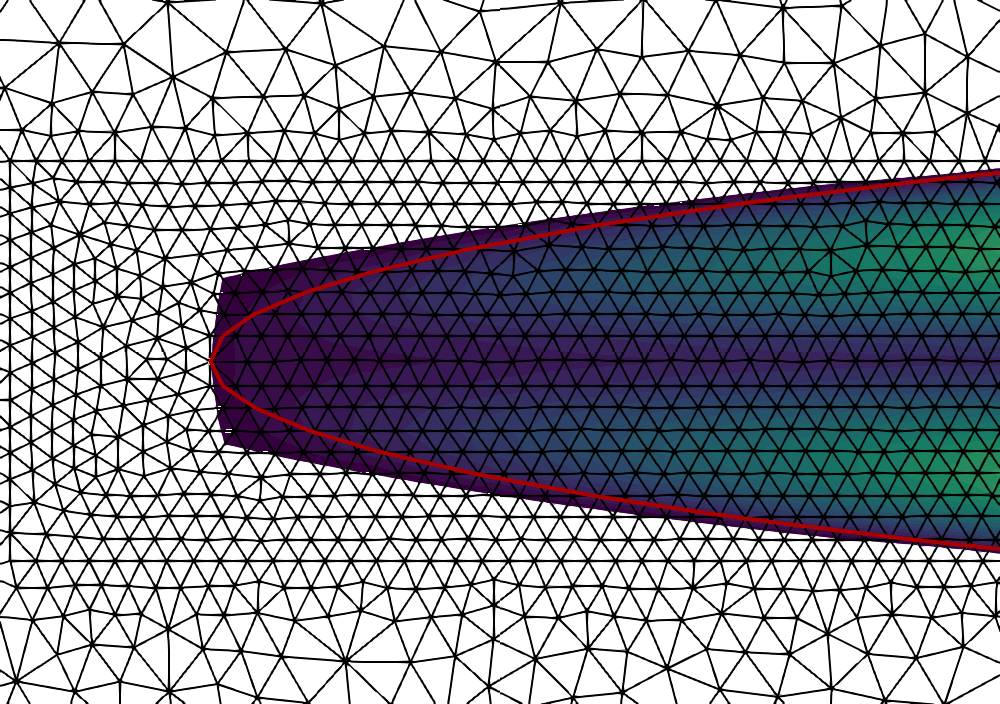
This work considers a Stokes flow in a deformable fracture interacting with a linear elastic medium. To this end, we employ a phase-field model to approximate the crack dynamics. Phase-field methods belong to interface-capturing approaches in which the interface is only given by a smeared zone. For multi-domain problems, the accuracy of the coupling conditions is, however, of utmost importance. Here, interface-tracking methods are preferred. The key objective of this work is to construct a robust framework that computes first a crack path via the phase-field method (interface-capturing) and then does an interface-tracking reconstruction. We then discuss several approaches to reconstruct the Eulerian description of the open crack domain. This includes unfitted approaches where a level-set of the crack interface is constructed and an approach where the geometry is re-meshed. Using this reconstructed domain, we can compute the fluid-structure interaction problem between the fluid in the crack and the interacting solid. With the explicit mesh reconstruction of the two domains, we can then use an interface-tracking Arbitrary-Lagrangian-Eulerian (ALE) discretisation approach for the resulting fluid-structure interaction (FSI) problem. Our algorithmic procedure is realised in one final algorithm and one program. We substantiate our approach using several numerical examples based on Sneddon's benchmark and corresponding extensions to Stokes fluid-filled regimes.