Summation-by-parts operators for general function spaces: The second derivative

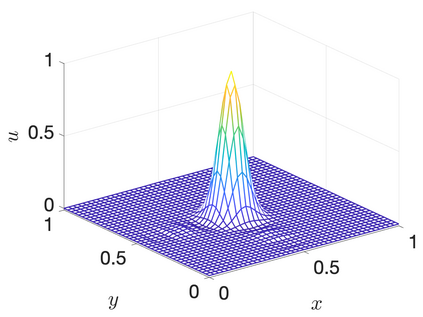
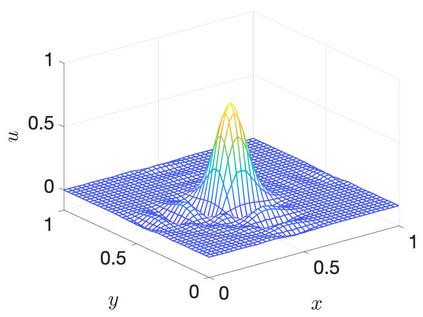
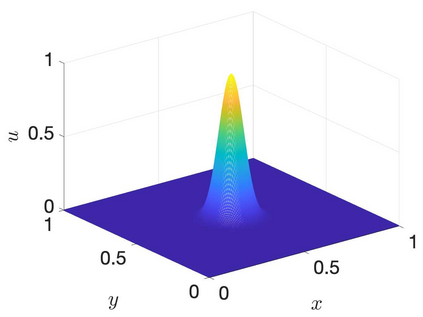
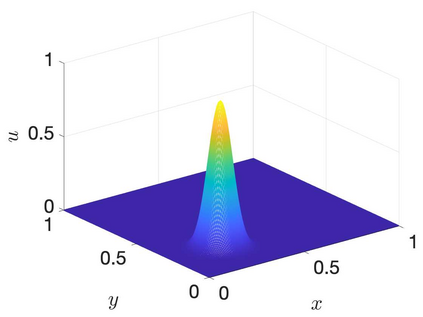
Many applications rely on solving time-dependent partial differential equations (PDEs) that include second derivatives. Summation-by-parts (SBP) operators are crucial for developing stable, high-order accurate numerical methodologies for such problems. Conventionally, SBP operators are tailored to the assumption that polynomials accurately approximate the solution, and SBP operators should thus be exact for them. However, this assumption falls short for a range of problems for which other approximation spaces are better suited. We recently addressed this issue and developed a theory for first-derivative SBP operators based on general function spaces, coined function-space SBP (FSBP) operators. In this paper, we extend the innovation of FSBP operators to accommodate second derivatives. The developed second-derivative FSBP operators maintain the desired mimetic properties of existing polynomial SBP operators while allowing for greater flexibility by being applicable to a broader range of function spaces. We establish the existence of these operators and detail a straightforward methodology for constructing them. By exploring various function spaces, including trigonometric, exponential, and radial basis functions, we illustrate the versatility of our approach. We showcase the superior performance of these non-polynomial FSBP operators over traditional polynomial-based operators for a suite of one- and two-dimensional problems, encompassing a boundary layer problem and the viscous Burgers' equation. The work presented here opens up possibilities for using second-derivative SBP operators based on suitable function spaces, paving the way for a wide range of applications in the future.