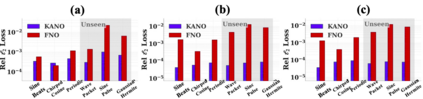
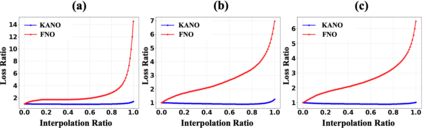
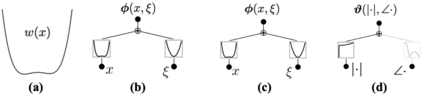
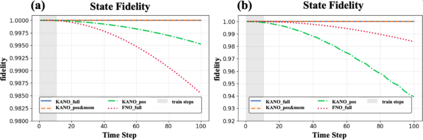
We introduce Kolmogorov--Arnold Neural Operator (KANO), a dual-domain neural operator jointly parameterized by both spectral and spatial bases with intrinsic symbolic interpretability. We theoretically demonstrate that KANO overcomes the pure-spectral bottleneck of Fourier Neural Operator (FNO): KANO remains expressive over generic position-dependent dynamics (variable coefficient PDEs) for any physical input, whereas FNO stays practical only for spectrally sparse operators and strictly imposes a fast-decaying input Fourier tail. We verify our claims empirically on position-dependent differential operators, for which KANO robustly generalizes but FNO fails to. In the quantum Hamiltonian learning benchmark, KANO reconstructs ground-truth Hamiltonians in closed-form symbolic representations accurate to the fourth decimal place in coefficients and attains $\approx 6\times10^{-6}$ state infidelity from projective measurement data, substantially outperforming that of the FNO trained with ideal full wave function data, $\approx 1.5\times10^{-2}$, by orders of magnitude.
翻译:暂无翻译