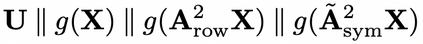Can we design a GNN that is accurate and interpretable at the same time? Could it also be robust to handle the case of homophily, heterophily, or even noisy edges without network effects? We propose SlenderGNN that has all desirable properties: (a) accurate, (b) robust, and (c) interpretable. For the reasons of its success, we had to dig deeper: The result is our GNNLin framework which highlights the fundamental differences among popular GNN models (e.g., feature combination, structural normalization, etc.) and thus reveals the reasons for the success of our SlenderGNN, as well as the reasons for occasional failures of other GNN variants. Thanks to our careful design, SlenderGNN passes all the 'sanity checks' we propose, and it achieves the highest overall accuracy on 9 real-world datasets of both homophily and heterophily graphs, when compared against 10 recent GNN models. Specifically, SlenderGNN exceeds the accuracy of linear GNNs and matches or exceeds the accuracy of nonlinear models with up to 64 times fewer parameters.
翻译:我们能否同时设计出一个既准确又可解释的GNNN? 是否还可以在不产生网络效果的情况下处理同质、 偏差甚至吵闹的边缘情况? 我们建议SlenderGNNNN, 其所有适当属性都具有:(a) 准确、 (b) 稳健和(c) 可解释性。 由于其成功的原因, 我们不得不更深入地挖掘: 结果是我们的GNNLin框架, 突出流行的GNN模型之间的根本差异( 如特征组合、 结构正常化等), 从而揭示出我们SlenderGNNNN成功的原因, 以及其他GNN变异体偶尔失败的原因。 由于我们精心设计, SlenderGNNNN通过了我们提出的所有“ 无害性检查 ”, 并且它实现了9个真实世界的同质和异质图形数据集的总精确度, 与最近的10个GNNNM模型相比。 具体地说, SlenderGNNNNN超过线 GN的精度, 和匹配或超过非线性模型的精确度,, 不到64 参数。