Solving the linear semiclassical Schrödinger equation on the real line

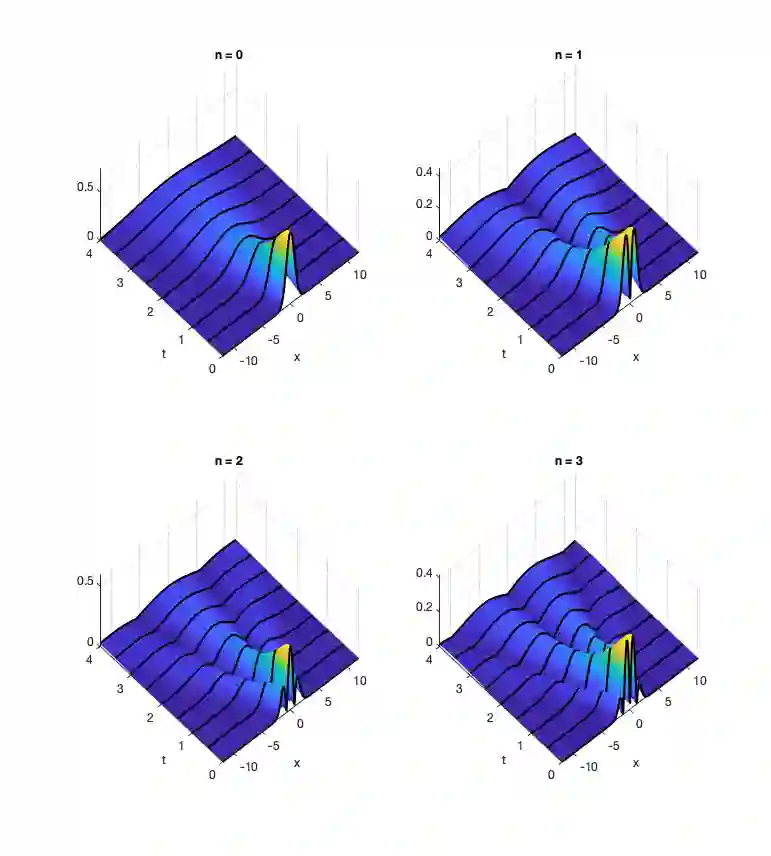
The numerical solution of a linear Schr\"odinger equation in the semiclassical regime is very well understood in a torus $\mathbb{T}^d$. A raft of modern computational methods are precise and affordable, while conserving energy and resolving high oscillations very well. This, however, is far from the case with regard to its solution in $\mathbb{R}^d$, a setting more suitable for many applications. In this paper we extend the theory of splitting methods to this end. The main idea is to derive the solution using a spectral method from a combination of solutions of the free Schr\"odinger equation and of linear scalar ordinary differential equations, in a symmetric Zassenhaus splitting method. This necessitates detailed analysis of certain orthonormal spectral bases on the real line and their evolution under the free Schr\"odinger operator.