On a risk model with tree-structured Poisson Markov random field frequency, with application to rainfall events

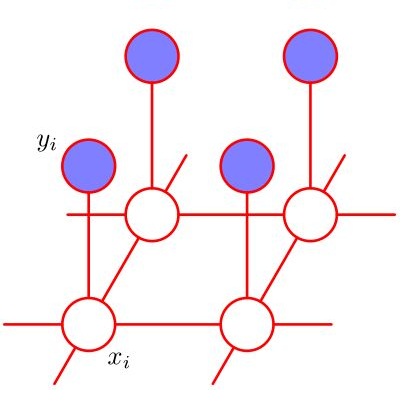
In many insurance contexts, dependence between risks of a portfolio may arise from their frequencies. We investigate a dependent risk model in which we assume the vector of count variables to be a tree-structured Markov random field with Poisson marginals. The tree structure translates into a wide variety of dependence schemes. We study the global risk of the portfolio and the risk allocation to all its constituents. We provide asymptotic results for portfolios defined on infinitely growing trees. To illustrate its flexibility and computational scalability to higher dimensions, we calibrate the risk model on real-world extreme rainfall data and perform a risk analysis.