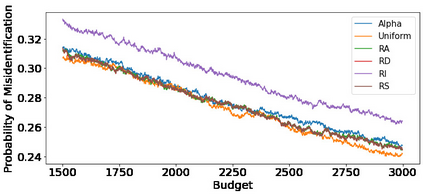
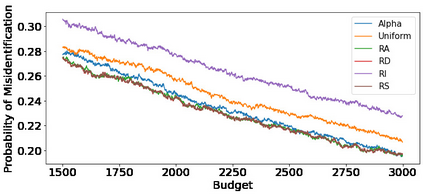
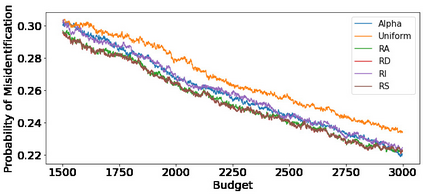
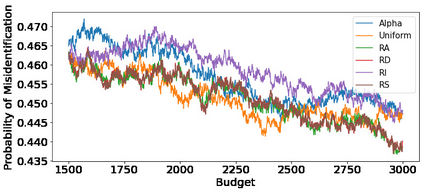
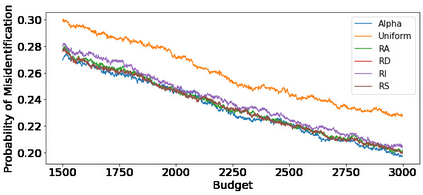
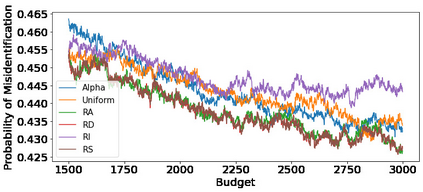
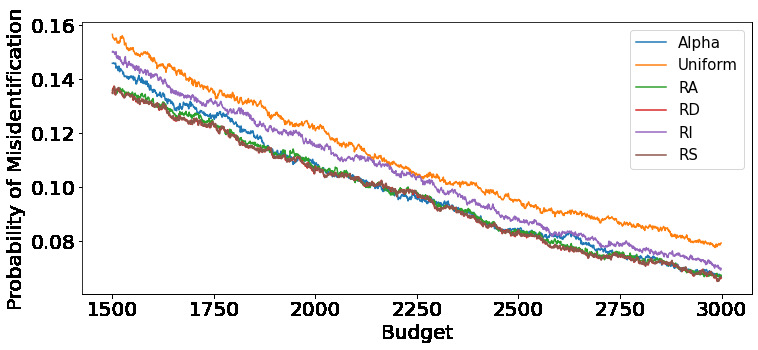
We consider fixed-budget best arm identification in two-armed bandit problems. One of the longstanding open questions is a tight lower bound on the probability of misidentifying the best arm and a strategy whose upper bound matches the lower bound when the optimal target allocation ratio of arm draws is unknown. We address this problem when the gap between the expected rewards is small. First, we introduce a distribution-dependent lower bound. Then, we propose the ``RS-AIPW'' strategy, which consists of the random sampling (RS) rule using the estimated optimal target allocation ratio and the recommendation rule using the augmented inverse probability weighting (AIPW) estimator. Our proposed strategy is optimal in the sense that the upper bound achieves the lower bound when the budget goes to infinity and the gap goes to zero. In the course of the analysis, we present a novel large deviation bound for martingales.
翻译:我们考虑在两只手的匪徒身上找到固定预算的最佳手臂。 长期未决问题之一是,误认最佳手臂的可能性和在未知道最佳手臂分配比例的情况下,其上界与下界相匹配的战略,其上界与下界相匹配; 当预期收益之间的差距很小时,我们解决这个问题; 首先,我们引入一个依赖分配的下界。 然后,我们提出“RS-AIPW”战略,它由随机抽样规则(RS)组成,使用估计的最佳目标分配比率,以及使用增加的反位概率加权(AIPW)的建议规则组成。 我们提出的战略是最佳的,因为上界在预算达到极限时会达到较低的界限,而差距则达到零。 在分析过程中,我们提出了一个新的大偏差,是用于马廷加勒。