【NTU博士论文】深度神经网络的参数高效推理与训练

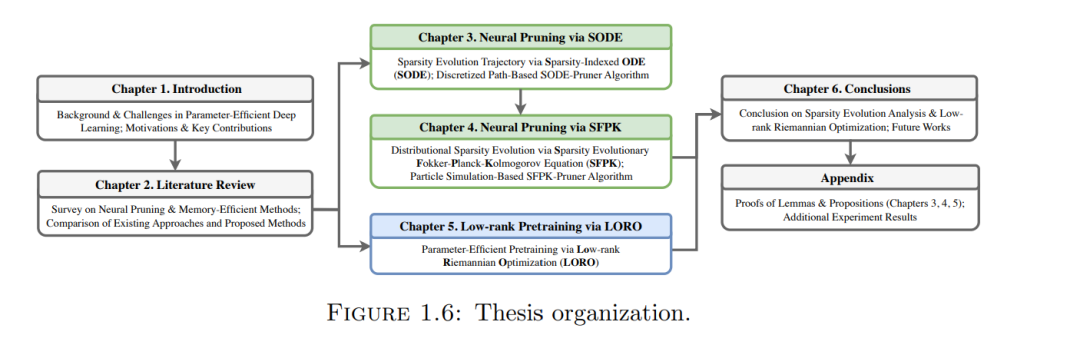
深度学习已成为在多个领域（如计算机视觉、自然语言与语音处理以及推荐系统）实现接近人类智能水平的核心范式。然而，随着深度学习模型性能的不断提升，其参数规模、内存占用和计算成本也显著增长，从而在资源受限设备上部署模型以及在实时推理场景中应用时带来了更大的挑战。因此，在提升模型性能的同时，提高推理和训练的效率同样至关重要。本论文聚焦于设计新颖的神经网络剪枝方法和参数高效优化算法，以在推理和训练过程中提升深度学习模型的效率。 本论文的第一部分着重于通过神经网络剪枝提升推理效率。神经剪枝是一种广泛应用的技术，旨在从预训练的深度神经网络中移除不重要的参数，以在给定稀疏性约束下找到最优的稀疏子网络。剪枝的关键挑战在于：高维子网络搜索空间的组合性质使得在高稀疏度下寻找最优子网络极其困难。已有工作大多尝试直接在目标稀疏水平估计最优子网络，但一个自然的问题是：如果我们已知稍低稀疏度下的最优子网络，能否更容易找到更高稀疏度下的最优子网络？ 换句话说，能否利用较低稀疏水平的最优子网络来指导更高稀疏水平的搜索？ 本论文从一个新颖的稀疏性演化（sparsity evolution）视角对此问题给出肯定回答：我们分析最优子网络如何随着稀疏度从零逐渐增加到目标水平而演化，从而能够逐步将未剪枝的稠密模型转化为任意稀疏度下的最优子网络。在第一项研究中，我们提出了稀疏性索引常微分方程（Sparsity-indexed ODE, SODE），这是一种向量形式的闭式 ODE，用于有效近似最优子网络在无限小稀疏度增量下的演化轨迹。基于此，我们实现了 SODE-pruner，通过 SODE 离散化逐步稀疏化预训练模型，并在多种场景下表现出与多种剪枝基线方法竞争的性能。然而，SODE 仅能建模单一剪枝轨迹，无法捕捉整个最优子网络族群的稀疏性演化。为更全面建模最优子网络的演化，本论文第二项工作从概率视角研究最优子网络族群的稀疏性演化。我们将神经剪枝重新表述为子网络分布上的期望损失最小化问题，并提出了一种有效的近似方法——稀疏性演化的 Fokker-Planck-Kolmogorov 方程（SFPK）。SFPK 是一种分布值闭式 ODE，用于模拟子网络分布在无限小稀疏度增量下的转移。基于此，我们提出了 SFPK-pruner，一种概率剪枝方法，它通过模拟子网络粒子系统的动态，从 SFPK 的终态分布中采样高性能稀疏子网络。在理论上，我们证明了 SFPK-pruner 的收敛性；在实践中，它在多种剪枝场景下展现出强大的经验性能。 尽管神经剪枝和其他模型压缩技术能够有效减少参数规模并提升推理效率，但对大模型（如大语言模型）的预训练仍然因其庞大的参数量而计算开销巨大。因此，本论文第二部分聚焦于设计参数与内存高效的语言模型预训练算法。一种有效提升训练和推理中参数效率的方法是：将每个全尺寸权重矩阵参数化为两个可训练低秩因子的乘积。然而，在严格的低秩约束下从零开始预训练仍具挑战，现有方法往往分别优化低秩因子，忽视了低秩参数空间的几何结构，同时引入了全梯度的冗余，最终阻碍表示学习。为实现高效且有效的低秩预训练，我们提出了 低秩黎曼优化器（Low-rank Riemannian Optimizer, LORO）。在每次 LORO 更新中，低秩因子对被联合更新，以确保其乘积矩阵沿着低秩流形上的最速下降方向移动，而无需计算任何占用内存的全尺寸权重矩阵或梯度。在实践中，LORO 能够找到性能与全尺寸预训练基线模型相当的低秩模型，同时显著降低内存使用并加速训练与推理。 综上所述，本论文提出了系统性的方法来提升深度学习模型在推理与训练两方面的效率：在推理端，我们提出 SODE 和 SFPK，有效近似最优子网络在稀疏性逐步增加过程中的演化；在训练端，我们提出 LORO，实现高效的低秩预训练，在显著降低内存和计算开销的同时保持了模型性能。这些贡献推动了深度学习模型在推理与训练效率优化方面的最新进展，使其更高效、更适用于实际应用。