Nature：大脑中的多时间尺度强化学习

摘要

为了在复杂环境中生存并获得成功，动物和人工智能体必须学会自适应地行动，以最大化适应度（fitness）和奖励（rewards）。这种自适应行为可以通过强化学习（reinforcement learning）习得，这类算法不仅在训练人工智能主体方面取得了成功，还在刻画中脑多巴胺能神经元（dopaminergic neurons）放电活动中发挥了作用。在经典强化学习模型中，智能体根据单一时间尺度（timescale）——即折扣因子（discount factor）——对未来奖励进行指数折扣。本文探讨了生物强化学习中多个时间尺度（multiple timescales）的存在。我们首先展示了在多重时间尺度上学习的强化学习智能体所具有的独特计算优势。随后，我们报道了在执行两种行为任务的小鼠中，多巴胺能神经元以多种折扣时间常数（discount time constants）编码奖励预测误差（reward prediction error）。模型解释了在由线索诱发的瞬时响应和称为多巴胺攀升（dopamine ramps）的更慢时间尺度波动中观察到的时间折扣异质性。更重要的是，单个神经元在两种任务中测得的折扣因子呈现高度相关性，表明这是一种细胞特异性（cell-specific）的属性。综合而言，我们的研究为理解多巴胺能神经元功能异质性提供了新的范式，并为人类和动物在多种情境下采用非指数折扣（non-exponential discounts）的经验观察提供了机理基础，同时也为设计更高效的强化学习算法开辟了新途径。

**

**

**关键词：多时间尺度、强化学习（Reinforcement Learning, RL）、奖励预测误差、折扣因子（Discount Factor）、价值函数、拉普拉斯变换（Laplace Transform）、多巴胺神经元（Dopaminergic Neurons）、时序编码（Temporal Representation）、神经异质性（Neuronal Heterogeneity）**********************************

彭晨丨作者

论文题目：Multi-timescale reinforcement learning in the brain 论文链接：https://www.nature.com/articles/s41586-025-08929-9 发表时间：2025年6月4日 论文来源：Nature

在复杂环境中，动物和人工智能系统都需学习如何在不确定的未来中做出最佳决策，以最大化回报。传统的时间差分强化学习（Temporal-Difference Reinforcement Learning）依赖于单一时间尺度的折扣因子（Discount Factor），将未来奖励按统一速率指数衰减。然而，行为经济学与生态学研究表明，人类与动物通常表现出非指数型折扣，例如超曲线折扣（Hyperbolic Discounting），并能根据环境不确定性灵活调整。最新发表于 Nature 的一项研究，从计算与神经生物学视角提出：大脑中的多巴胺系统或通过多种时间尺度并行学习，实现更高效、更灵活的强化学习机制。

**

**

多时间尺度RL的计算优势

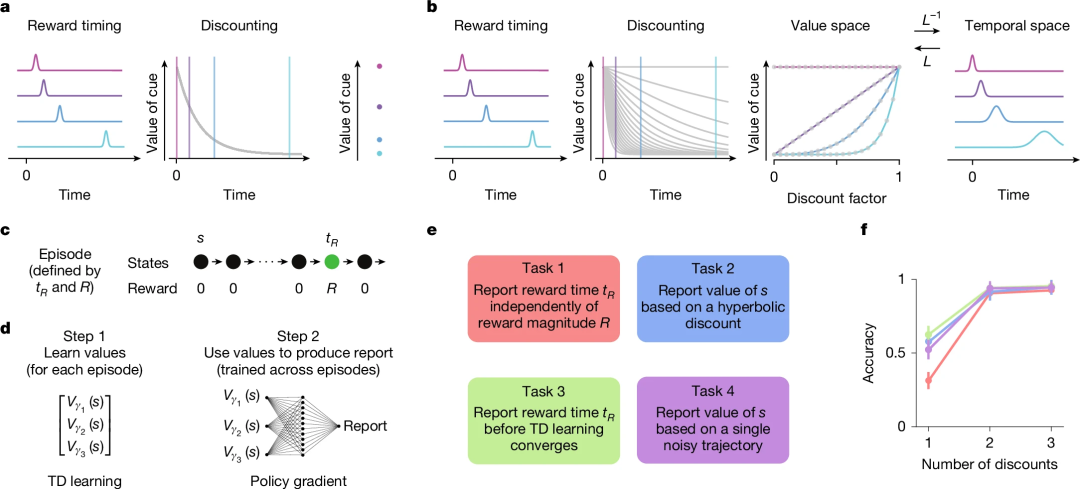
研究团队首先使用模型仿真比较了单一时间尺度与多时尺度强化学习的表现差异。以一个线性迷宫为例，智能体在每次试验中都会在起点收到提示信号，然后在特定时刻获得奖励。传统只采用单一折扣因子，奖励大小与时延信息通常被压缩到同一个标量中。而当引入多个折扣因子（γi）并行学习时，智能体对不同时间窗内的奖励预期形成向量化表示（如公式所示）。 研究团队首先在仿真环境中对比了单一折扣因子与多时尺度价值表征的性能差异，使用了四个任务（图1e）。在“解耦奖励大小与时间”（Task 1）中，单一折扣因子模型无法区分价值是来自于“小额近期奖励”与“大额远期奖励”，而多时尺度系统则通过折扣价值谱（value spectrum）的形状不变性，可以将奖励时间与奖励幅度相分离。进一步地，多时间尺度系统隐含了所有未来时刻的指数折扣值，使其能够在同一表征上灵活重加权，以重现超曲线折扣（Task 2），甚至在学习尚未收敛时，就从折扣谱形状中推断出奖励时延（Task 3），并可根据当前状态在“近视”与“远见”间切换以优化不完全学习场景下的决策（Task 4）。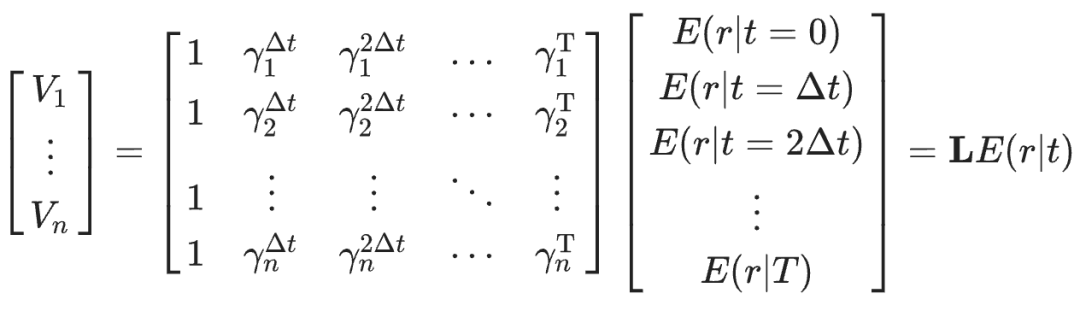

图 1. 多时间尺度强化学习的计算优势。a. 在单时间尺度价值学习中，预测未来奖励的线索（在 t = 0 时）的价值（左）通过单一指数折扣函数对这些奖励进行折扣来评估（中）。预期奖励的大小和时间被编码在线索的价值中，但两者相互混淆（右）。b. 在多时间尺度价值学习中，相同的奖励延迟通过多个折扣函数进行评估（中左）。线索的相对价值作为折扣的函数取决于奖励延迟（中右）。因此，基于拉普拉斯变换的简单线性解码器可以重建奖励的预期时间和大小（右）。c. 比较单时间尺度与多时间尺度学习的实验。tR 和 R 在每个episode中固定，但在不同episode中变化。d. 步骤 1：在每个episode中，价值函数通过使用多个折扣因子的表格更新来学习。给定这些值，步骤 2 包括训练一个非线性解码器以最大化任务特定报告的准确性。解码器通过策略梯度在不同情节中进行训练。e. 该架构在四项任务中进行训练，以突显多时间尺度强化学习的计算优势，包括将奖励大小和奖励时间的信息解耦、能够使用任意折扣函数进行学习、能够在收敛前恢复奖励时间信息以及能够控制归纳偏差（见正文和方法部分）。f. 在 2000 次训练回合后报告平均准确率，作为正确响应的比例。“三个折扣”对应于 [0.6, 0.9, 0.99] 的集合，“一个折扣”对应于在 {[0.6, 0.6, 0.6], [0.9, 0.9, 0.9], [0.99, 0.99, 0.99]} 中表现最佳的集合，“两个折扣”情况类似。

**

**

多巴胺神经元中的折扣特性

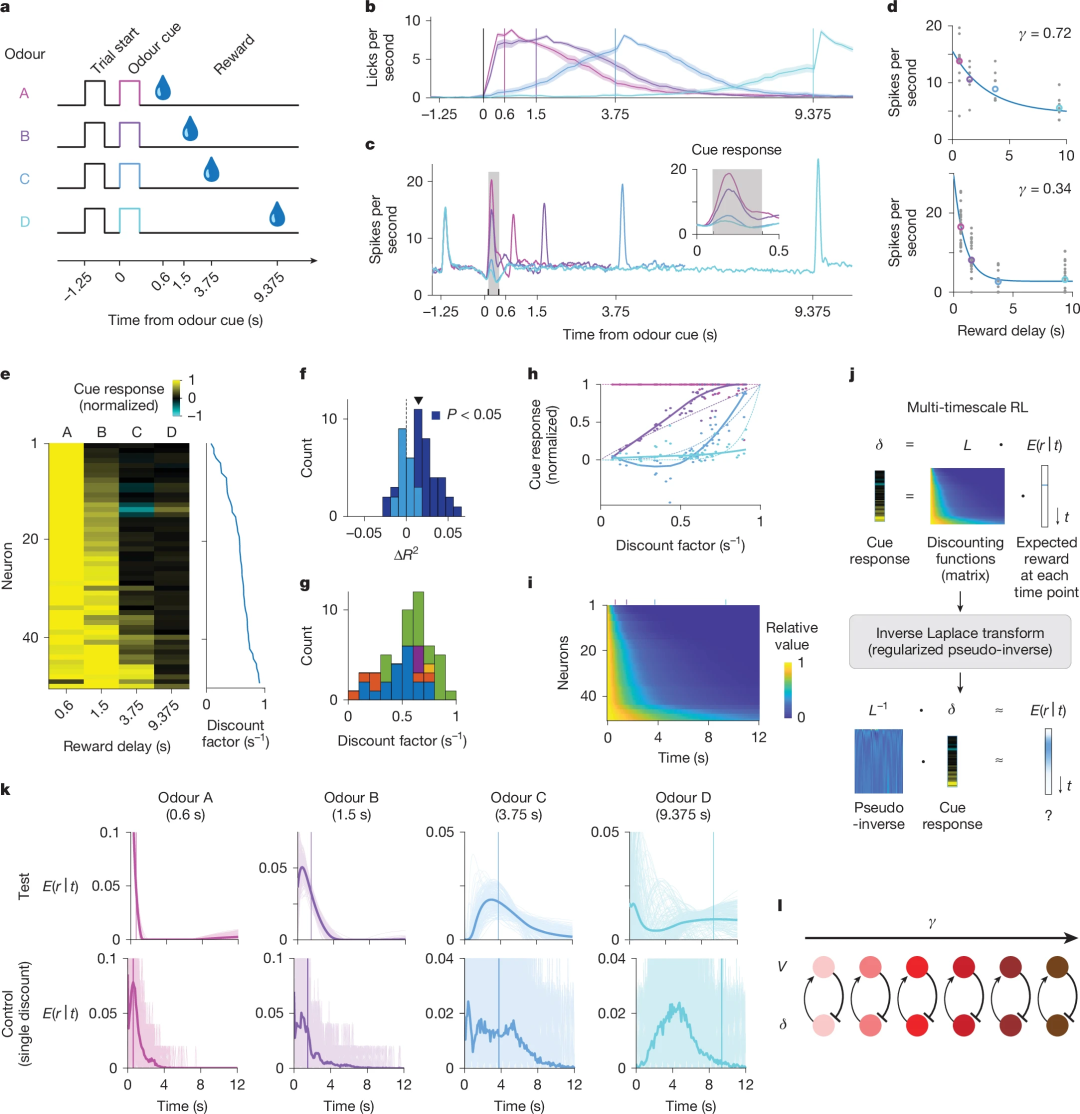
紧接着，研究团队在小鼠中进行了两类行为任务的电生理记录。其一是「气味延迟任务」（Cued Delay Task），每个气味线索对应不同的水奖励时延；其二是在虚拟现实线性跑道中，动物需在行进接近目标时获得奖励。 研究发现，位于腹侧被盖区（VTA）的多巴胺神经元对提示信号的瞬时响应幅度随预期奖励时延而异，且单个神经元的响应随时延衰减曲线服从指数模型而非超曲线模型，但在群体中呈现广泛的折扣因子分布——有神经元更偏向「近视」（高折扣率），有则偏向「长远」（低折扣率），形成多样性的折扣谱。这一特性不仅解释了为何整体行为表现出超曲线折扣，也为大脑如何同时编码多时尺度奖励预测误差提供了神经基础。

图 2. 多巴胺能神经元表现出多种折扣因子，使解码奖励延迟成为可能。a. 有提示延迟任务图示。b. 奖励发放前的预期舔舐行为。c. 四种试验类型的平均脉冲时序直方图。d. 两个单个神经元的示例提示反应拟合。e. 神经元群体的标准化提示反应。对于每个神经元，其反应被标准化为四种可能延迟中的最高反应。插图显示了每个神经元的推断折扣因子。f. 数据更符合指数模型而非双曲线模型。g. 神经元中推断折扣因子的分布（自助法的平均折扣因子）。h，归一化群体反应的形状与奖励延迟的关系。粗线表示平滑拟合，虚线表示理论值，点表示单个神经元。i，折扣矩阵。神经元的排序如图 d 所示。j，解码过程概述。k，未来奖励的主观预期时间可以从预测奖励延迟的提示的群体反应中解码出来。基于测试数据的提示平均反应的解码（上行；见方法）优于使用具有单一折扣因子的模型（群体平均折扣因子；下行；细线（浅阴影）表示单个自助样本的预测，粗线（浅阴影内的深阴影）表示自助样本的平均预测，单个深垂直线表示奖励时间；见方法；扩展数据图 4e）。l，每个多巴胺能神经元的 RPE 对一个独特的价值函数做出贡献的模型（见方法；扩展数据图 7f-k）。

**

**

渐进性攀升及其多时间尺度解释

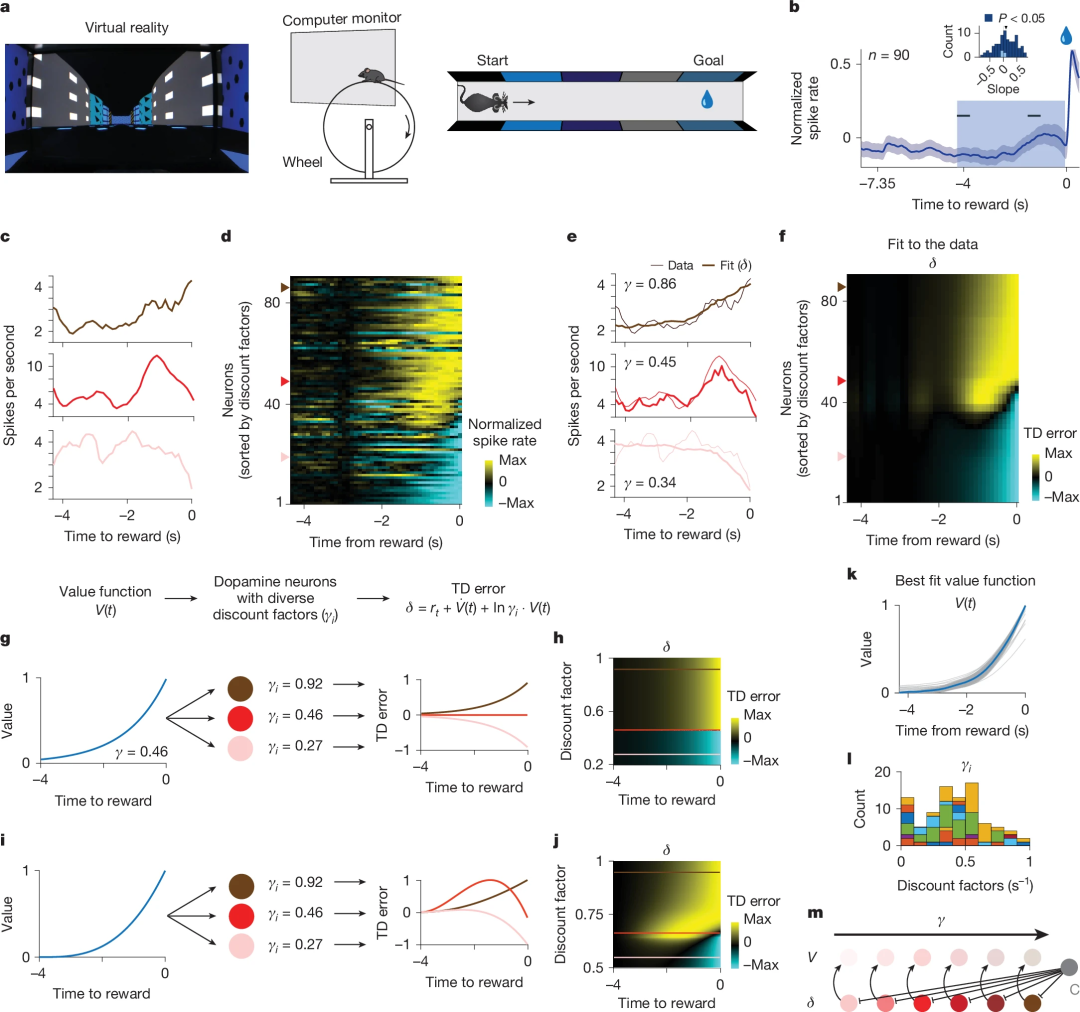
在更自然的任务场景中，多巴胺信号往往表现为沿目标接近而平滑上升的“递进性攀升（Dopamine Ramping）”。此前对该现象的解释多聚焦于逐步累积的奖励预测误差或路径积分等，然而本研究指出，只需假定神经元共享一个“共同的价值函数”，并各自采用不同折扣因子，对该函数在时间上的导数进行指数折扣响应，就能再现多种攀升形态：有的神经元持续上升，有的先降后升，甚至有的下降趋势（图 3c）。换言之，攀升多样性可被视为多时间尺度编码与单一价值函数交互的解码结果，无需假设多个独立系统。

图 3. 不同多巴胺神经元的折扣因子多样性解释了不同的攀升表现。a. 实验装置。虚拟现实走廊在运动开始时的视图（左）。实验装置示意图（中、右）。b. 单个多巴胺能神经元（n = 90）的平均活动在奖励发放前轨道的最后几秒内呈上升趋势。c. 在接近奖励的最后阶段表现出不同上升活动的单个神经元示例，包括单调上升（深红色）、非单调（红色）和单调下降（浅红色）上升。d. 整个神经元群体中的单个神经元在递增活动方面表现出多样性的谱系。神经元根据从共同价值函数模型推断出的折扣因子进行排序（图 k）。e. 图 c 中所示单个神经元的示例模型拟合。f. 模型捕捉到了整个群体中递增活动的多样性。神经元的排序方式与图 d 相同，依据的是推断出的折扣因子。g、h. 指数价值函数的折扣因子与递增多样性之间的关系。i、j. 三次价值函数的折扣因子与递增多样性之间的关系。k. 推断出的价值函数。灰色细线表示每次自助抽样推断出的价值函数。蓝色粗线表示自助抽样的平均值。l. 推断出的折扣因子直方图。

**

**

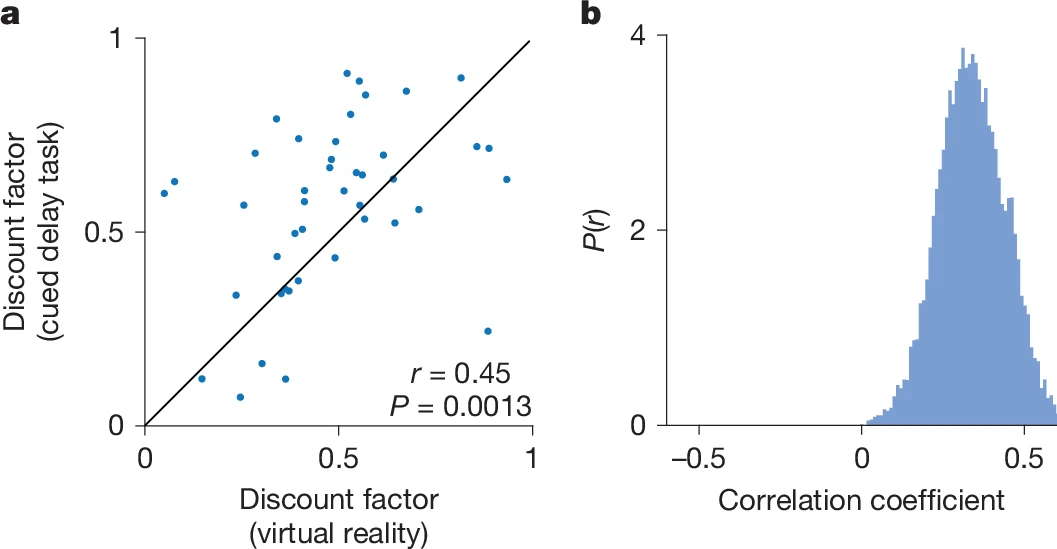
跨任务相关的折扣因子稳定性

为探究折扣因子的稳定性与任务依赖性，研究者对同只小鼠的同一神经元，在两种任务中分别拟合折扣谱并进行相关性分析。结果表明，折扣参数在“气味延迟任务”与“虚拟现实任务”中高度一致（Spearman ρ≈0.9），并通过自举分析验证了其统计学的鲁棒性。这一发现既支持了单细胞折扣特性的固有性，也为未来在人工智能中引入“元学习折扣因子”或“状态依赖折扣”提供了神经回路层面的借鉴。

图 4.单个多巴胺能神经元的折现因子在不同的行为下是相关的。

**

**

结语与展望

本项研究通过严谨的计算仿真与电生理实验结合，提出并验证了“大脑或利用多时尺度价值表征，通过向量化预测误差实现灵活决策”的新范式。其核心在于，神经系统在单元层面采用多样化指数衰减编码未来奖励时序，再由下游电路或拉普拉斯逆变换等方式解码，以获得精准的奖励时机与大小信息，兼容超曲线折扣与递进性攀升等多种行为神经现象。该工作不仅深化了对多巴胺系统功能异质性的理解，也将激发人工智能领域在深度强化学习中发展更高效、更稳健的多时尺度算法，为在自然环境中面临更复杂时序不确定性的智能体决策提供新的思路。