【纽约大学】贝叶斯深度学习和泛化性的概率观点，附27页PDF下载

【导读】纽约大学的Andrew Gordon Wilson和Pavel Izmailov在论文中从概率角度的泛化性对贝叶斯深度学习进行了探讨。贝叶斯方法的关键区别在于它是基于边缘化，而不是基于最优化的，这为它带来了许多优势。

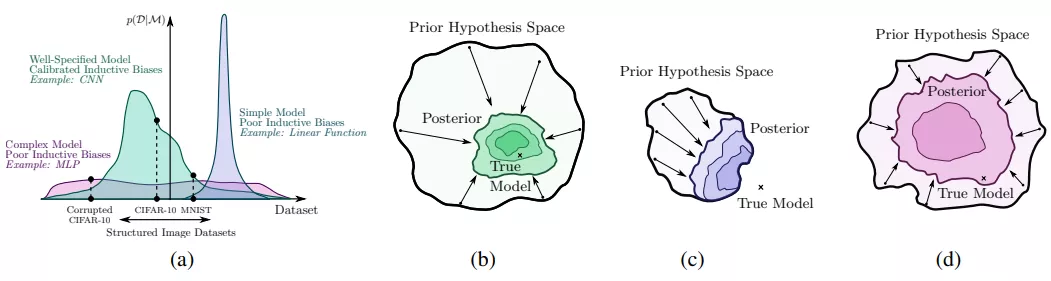
贝叶斯方法的关键区别是边缘化，而不是使用单一的权重设置。贝叶斯边缘化可以特别提高现代深度神经网络的准确性和校准，这是典型的不由数据完全确定，可以代表许多令人信服的但不同的解决方案。我们证明了深度集成为近似贝叶斯边缘化提供了一种有效的机制，并提出了一种相关的方法，通过在没有显著开销的情况下，在吸引域边缘化来进一步改进预测分布。我们还研究了神经网络权值的模糊分布所隐含的先验函数，从概率的角度解释了这些模型的泛化性质。从这个角度出发，我们解释了那些对于神经网络泛化来说神秘而独特的结果，比如用随机标签来拟合图像的能力，并证明了这些结果可以用高斯过程来重现。最后，我们提供了校正预测分布的贝叶斯观点。