微分编程:传统自动微分的"三宗罪"
加入极市专业CV交流群,与6000+来自腾讯,华为,百度,北大,清华,中科院等名企名校视觉开发者互动交流!更有机会与李开复老师等大牛群内互动!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 ,回复 加群,立刻申请入群~
作者:Leo
知乎链接:https://zhuanlan.zhihu.com/p/105662113
本文已由作者授权转载,未经允许,不得二次转载。
微分编程,或者说万物皆可微分是人类的伟大梦想之一,它的含义是:
对任意程序,在没有额外知识的介入的前提下,计算机可以通过自动化的计算得到程序输入对程序输出的导数。
导数在控制系统,科学计算和机器学习中扮演着核心的角色,通过微分编程“廉价”地获取导数对很多领域的数值计算有着方法论层面的提升。
这篇文章首先概括性的介绍传统自动微分的几种方案,接着讨论为何它们仍然称不上是微分编程以及它们的“三宗罪”,为后面介绍可逆图灵机上的自动微分的实现铺垫。
传统自动微分
一个可微分的计算模型可以描述为 。考虑一个计算过程
其中 , , 是计算过程的“深度”。这个计算过程的一阶导数是一个大小为 的Jacobian矩阵 ,其中 和 分别是输入和输出中的一个元素。
用程序自动化推导Jacobian矩阵或者其中的一部分叫做自动微分 (AD),大致可分为三类,tangent mode AD,adjoint mode AD和mixed mode AD。[Hascoet2013]
tangent mode AD可以在一次程序计算中通过链式法则 递推得到Jacobian矩阵中与单个输入有关的部分,或者说是Jacobian矩阵的一列(图一)。
这种AD实现起来很简单 [Revels2016],也不需要很多额外的内存空间。但是它在变分优化中用的并不多,因为在变分算法中,Loss只有一个但可变分的参数很多,比如机器学习模型中的参数个数经常有 数量级之多。
对于每个输入tangent mode AD都需要遍历计算过程以得到它的导数,重复遍历计算过程 次显然是无法接受的,于是86年Hinton提出了用后向传播技术训练神经网络 [Rumelhart1986],也就是接下来要说的adjoint mode AD。
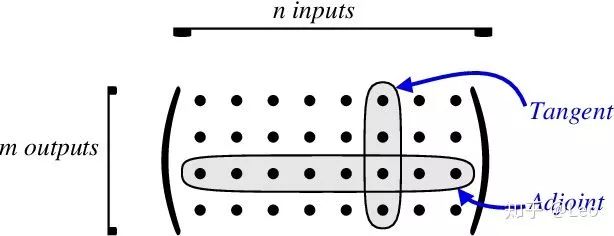
adjoint mode AD利用链式法则 可以仅通过一次对计算过程的遍历得到Jacobian矩阵的一行。
但它的导数链式法则传递方向和程序执行方向相反,所以需要在程序计算过程中记录一些额外的信息来辅助求导,这些辅助信息包括计算图和计算过程的中间变量。计算图是一个有向无环图(DAG),它表达了函数和变量的关系。
在现今主流的自动微分框架Pytorch [Paszke2017]和Flux.jl [Innes2018]中,程序在执行的时候把计算图信息记录在一个叫做“张量”的变量中。每个张量都有一个叫做tracker的结构体(实现细节见@罗秀哲的「一天实现自己的自动微分」,https://zhuanlan.zhihu.com/p/47592565),它记录了产生这个张量的过程,包括函数和函数的输入(父节点)。
在TensorFlow [Tensorflow2015]中,用户必须在执行前构造静态图,而中间结果也被记录在这个静态图中。
Julia下的源到源的自动微分工具Zygote [Innes2018, Innes2019]用程序的static single assignment (SSA) 这种中间表示当做计算图,中间变量存放在全局的链表中(实现细节见@罗秀哲
的「一天实现你自己的源到源自动微分」,https://zhuanlan.zhihu.com/p/75916086)。
第三种mixed mode AD是以上两种AD的混合。
接下来我们会着重讨论应用最为广泛的adjoint mode AD,它对计算图的依赖和对中间结果的记录方式导致了下面我们要控诉的三宗罪。
传统AD的“三宗罪”
其一,自动微分不自动。
程序员们往自动微分库里面加入了一些已知函数的自动微分规则,包括exp函数,矩阵乘法等基础函数的向后传播规则来帮助我们写可微分的代码。我们称这些定义了求导规则的函数为primitive。
虽然在主流机器学习框架中定义了很多常用函数,但我们仍然经常觉得不够用。
比如在物理中应用广泛的奇异值分解(SVD)函数 [Seeger2017,Hubig2019]的adjoint rule在很长时间内都没有被重视。SVD的复数版本自动微分规则的推导是最近一年才被研究透彻 [Wan2019],耗费了很多科研工作者的精力。
近些年SVD的微分技术的发展给多体物理中应用广泛的张量网络技术带来了新的突破[Liao2019]。
比如在张量重整化群(TRG)程序就涉及到SVD的自动微分,对TRG程序求一阶导数可以得到能量密度,求二阶导可以得到比热容,自动微分避免了差分法带来的数值误差。
Corner transfer matrix重整化群 (CTMRG)中也用到了SVD,通过自动微分求导来训练一个张量网络态可以大大减少计算时间和人力成本。
除了SVD的求导,还有关于最大或最小本征求解器的微分,19年这个技术的突破使得我们可以去用Fidelity Susceptibility来判断相变点 [Xie2020]。
类似的例子还有在控制系统中有着重要应用的神经网络积分器(Neural ODE)[Chen2018]和量子模拟中对参数化的量子门的微分[Luo2019]。
我们发现每个重要的primitive的求导规则的发现和成熟,总伴随着一些重要的应用。
但不得不吐槽的是,自动微分也太不自动了,导致我们手动定义了太多的primitive,和我们理想中的万物皆可微分的微分编程相去甚远。
要知道所有函数最终都会编译到基本指令,包括加减乘除,布尔代数,还有条件跳转语句等。这些指令都很简单,只要实现这些基本指令的微分,就应该可以做到万物皆可微分,包括上面所说的线性代数的自动微分。
现在的自动微分框架不自动的本质原因并不是没法对计算机指令构成的计算图定义自动微分,而是这么定义后计算性能会差至少两个数量级,也就没有实际价值了。
Julia中可以通过 @code_native 宏获得一个代码最终编译到的汇编指令,分析这些指令可以得到一个由指令构成的“计算图”。考虑如下代码(可在Julia REPL中执行)
julia> function f(x)
while x < 100
x = x * 1.5
end
end
f (generic function with 1 method)
julia> @code_native f(1.0)
.text
; ┌ @ REPL[15]:2 within `f'
movabsq $22888461284808, %rax # imm = 0x14D1229AB5C8
; │┌ @ float.jl:503 within `<' @ float.jl:458
vmovsd (%rax), %xmm1 # xmm1 = mem[0],zero
vucomisd %xmm0, %xmm1
; │└
jbe L58
movabsq $22888461284816, %rax # imm = 0x14D1229AB5D0
vmovsd (%rax), %xmm2 # xmm2 = mem[0],zero
nopw %cs:(%rax,%rax)
; │ @ REPL[15]:3 within `f'
; │┌ @ float.jl:405 within `*'
L48:
vmulsd %xmm2, %xmm0, %xmm0
; │└
; │ @ REPL[15]:2 within `f'
; │┌ @ float.jl:503 within `<' @ float.jl:458
vucomisd %xmm0, %xmm1
; │└
ja L48
; │ @ REPL[15]:3 within `f'
L58:
retq
nopl (%rax,%rax)
; └
AD框架就会把代表乘法的“vmulsd %xmm2, %xmm0, %xmm0”这个操作记录在计算图中,并把输入“%xmm0”的数值记录在缓存空间中辅助求导。
这种每做一个指令都缓存的方法用到SVD算法中就不实际了,因为SVD算法中乘法操作的数目随矩阵维度 是 的关系,这种频繁的访存带来了至少两个数量级的性能损失。
不仅基本算数指令是问题,这里的流控制也是个大问题。这里的流控制最终被编译到了条件跳转(jump if)语句“ja L48”指令,而条件跳转语句在通常AD框架的处理中需要被展开而变得非常不高效。
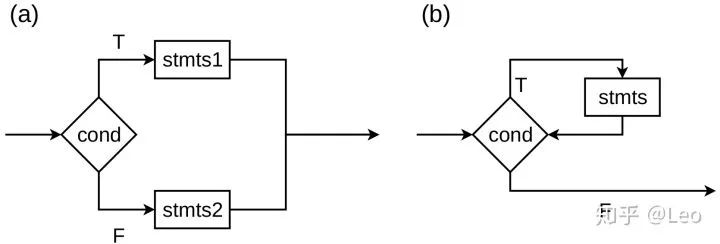
如图图二(b) 中描述的while语句,当条件cond为真 (T),则执行stmts否则跳出循环。实际操作中,如果循环进行了n次,大多数AD框架会在计算图中记录n次vmulsd指令,于是计算图可能会比代码的长度长很多。
因此必须解决计算图的流控制和中间结果缓存的问题,才能让自动微分自动起来。
其二,内存墙问题。
传统机器学习库写出的程序的内存消耗一般随着程序运行时间线性的增加,这源于机器学习库的缓存中间状态的机制。
前文我们探讨到,为了帮助adjoint mode AD求导,必须缓存计算过程中的中间状态。
大多函数缓存的方式是记录输入值,因此随着计算时间的增加,需要记录的输入值也会线性增加。为了防止记录的值被篡改,在计算图中大多数情况不允许出现inplace函数(不分配新内存而直接改变旧内存空间中的内容的函数),从而导致内存和计算时间上更多的额外开销。
更糟糕的是,机器学习经常用到GPU来做训练,虽然GPU的计算能力很强,但是内存空间比起系统内存并不充沛。
下面的在一台GPU服务器上运行nvidia-smi得到的结果。可以看到一张计算能力突破100TFLOPS的Nvidia Tesla V100显卡只有32G内存,而对一个CPU集群而言,同样的算力内存可能会有PB级别之多。
jgliu@delta105:~$\$$ nvidia-smi
Fri Feb 7 17:33:04 2020
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 418.87.01 Driver Version: 418.87.01 CUDA Version: 10.1 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla V100-SXM2... Off | 00000000:1A:00.0 Off | 0 |
| N/A 43C P0 143W / 300W | 3143MiB / 32480MiB | 77% Default |
+-------------------------------+----------------------+----------------------+
| 1 Tesla V100-SXM2... Off | 00000000:1B:00.0 Off | 0 |
| N/A 41C P0 110W / 300W | 1546MiB / 32480MiB | 44% Default |
+-------------------------------+----------------------+----------------------+
| 2 Tesla V100-SXM2... Off | 00000000:3D:00.0 Off | 0 |
| N/A 34C P0 67W / 300W | 3060MiB / 32480MiB | 31% Default |
+-------------------------------+----------------------+----------------------+
| 3 Tesla V100-SXM2... Off | 00000000:3E:00.0 Off | 0 |
| N/A 29C P0 57W / 300W | 1120MiB / 32480MiB | 16% Default |
+-------------------------------+----------------------+----------------------+
| 4 Tesla V100-SXM2... Off | 00000000:88:00.0 Off | 0 |
| N/A 32C P0 40W / 300W | 11MiB / 32480MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 5 Tesla V100-SXM2... Off | 00000000:89:00.0 Off | 0 |
| N/A 29C P0 40W / 300W | 11MiB / 32480MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 6 Tesla V100-SXM2... Off | 00000000:B2:00.0 Off | 0 |
| N/A 30C P0 39W / 300W | 11MiB / 32480MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 7 Tesla V100-SXM2... Off | 00000000:B3:00.0 Off | 0 |
| N/A 26C P0 40W / 300W | 11MiB / 32480MiB | 0% Default |
+-------------------------------+----------------------+----------------------+在Recurrent Neural Network (RNN) [Lipton2015]和残差网络 [He2016]这些应用中, 网络深度经常可以上千,这时候内存墙问题 [1]是一个重要的计算瓶颈。
那么存储每一步的计算结果是否真的有必要?答案是否定的。
有两种基本的策略去避免存储每一步的计算结果。
第一种是图三 (a)中所示的checkpointing技术,它选择性的存储一部分函数的输入,比如图中 的数据被缓存了,但是 的数据却没有。
反向传播的时候,当程序发现
没有被缓存,就会调用
来重新计算出新的
。虽然多了一次计算,但是用作缓存的内存消耗减少了,或者说是用时间交换空间。
第二种是图 (b)所示的利用可逆primitive的做法,可逆primitive包括幺正矩阵,可逆激活函数等。当程序发现 是可逆函数,而 没有被缓存,就会利用 来计算得到 。
这里同样使用了时间交换空间的做法,这种交换方式我们称之为uncomputing。
在研究中,可逆技术包括information buffer方案构造的可逆乘除法 [Maclaurin2015]和可逆激活函数 [Gomez2017,Jacobsen2018]等大大提升了RNN [MacKay2018]和残差网络等应用的内存效率 [Behrmann2018]。
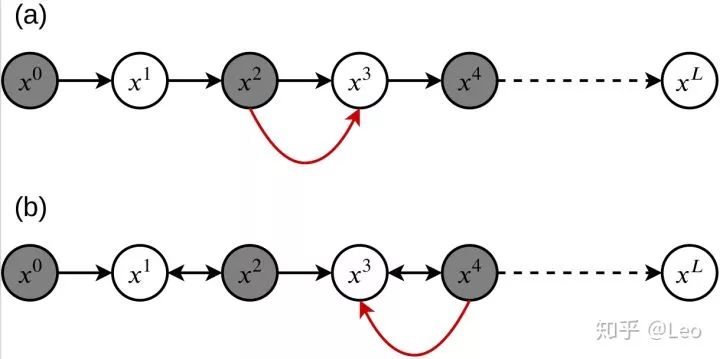
图三:两种在机器学习中常见的减少内存消耗的方式,(a) checkpointing技术,(b) 利用可逆primitive。图中,圆形节点代表了数据,灰色节点是其中被缓存的数据。黑色箭头是前向计算过程中的函数,双向箭头↔代表了可逆函数。红色箭头代表了向后传播过程中,计算出x3所使用的函数。
然而上述两种方案并不是系统性的解决方案,内存墙问题仍然制约着很多实际的应用,对这个问题的解决需要我们有对时间和空间的交换有更加本质的理解。
其三,低效的高阶导数。
高阶导数可以通过对低阶导数的求导来获得,比如在现有的绝大多数AD框架中,我们经常对一阶导微分来获得二阶导。
对于adjoint mode AD,一阶导数的计算需要遍历计算图两次,对它的求导需要把整个计算过程再遍历两次,因此一共遍历原始计算图4次。
以此类推, 阶导数需要遍历计算图 次。
其实这种递归遍历并非必要,一种更加有效的求解任意阶导数的方式叫做Taylor Propagation,一个函数的泰勒级数展开本身就可以定义adjoint规则来求导。
在JAX中就有关于Taylor Propagation的实现 [Bettencourt2019],但是这种实现依赖手动定义很多的adjoint规则,实际工作量会很大。
我们定义了太多的primitive,导致在拓展成本很高,能做指令级别的自动微分,这个问题也能迎刃而解。
总结
本文介绍了两种自动微分tangent mode AD和adjoint mode AD的基础理论,并“痛斥”了市面上的adjoint mode AD库不完善的地方。
后记
根据@罗秀哲同学的建议,针对文中的一些表述作一些comment:
1. Pytorch并非完全不支持inplace操作,当Pytorch发现一个tensor的引用计数为0,就允许inplace操作。
但这种情况多出现在tensor初始化,或者计算图的叶子节点上。
2. 有些情况下,指令级别的微分是帮不上忙的,比如sampling和斐波那契数列的递归计算。
参考文献
算法推导核心!一次性梳理清楚,是时候搞定矩阵求导了!
AAAI-20 Oral | 旷视研究院提出可微分二值化,实现文字检测精度速度双重最佳
高达82 fps的实时文本检测,华科AAAI2020提出可微分二值化模块