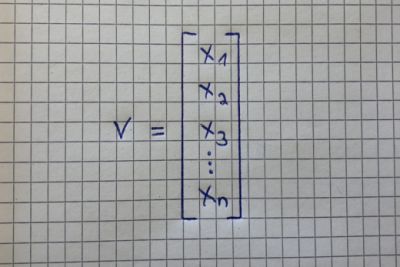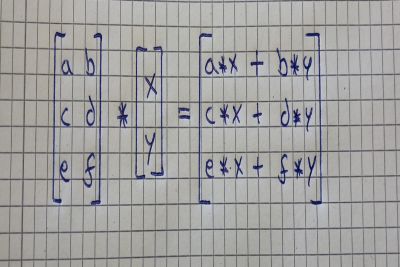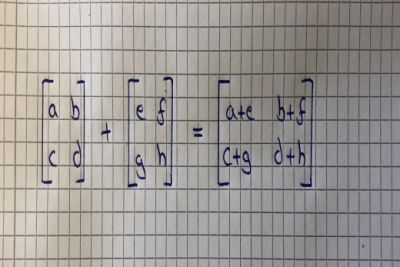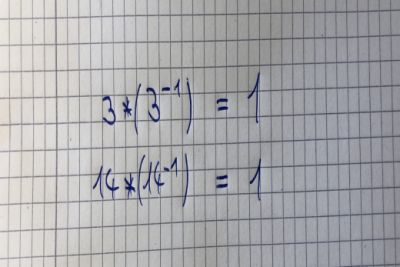【干货】​深度学习中的线性代数

【导读】近日，机器学习专业学生 Niklas Donges 撰写了一篇关于深度学习需要的数学基础相关知识。线性代数对于理解机器学习和深度学习内部原理至关重要，这篇博文主要介绍了线性代数的基本概念，包括标量、向量、矩阵、张量，以及常见的矩阵运算。本文从一个直观、相对简单的角度讲解了线性代数中的概念和基础操作，即使您没有相关的基础知识，相信也很容易理解。

编译 | 专知

参与 | Yingying

深度学习中的线性代数

 

学习线性代数对理解机器学习背后的理论至关重要，特别是对于深度学习。 它让您更直观地了解算法是如何工作的，从而使您能够做出更好的决策。 本文将介绍用于机器学习的一些线性代数概念。

▌简介

---

---

线性代数是一种连续的数学形式，它在整个科学和工程中被广泛应用，因为它允许对自然现象进行建模并高效计算。线性代数也是几乎所有数学领域的核心。它是理解机器学习背后理论的关键，尤其是深度学习。在开始使用机器学习之前，您不需要了解线性代数，但是在某些时候，您需要更好地理解不同机器学习算法的工作原理。这将有助于您在机器学习系统的开发过程中做出更好的决策。所以，如果你真的想成为这个领域的专家，你必须理解线性代数。在线性代数中，数据由矩阵和向量的形式的线性方程表示。因此，你主要处理的是矩阵和向量，而不是标量（我们将在下一节介绍这些术语）。如果您使用像Numpy这样的库，则只需几行代码即可轻松计算复杂的矩阵乘法。请注意，这篇博文忽略了对机器学习不重要的线性代数的概念。

▌数学对象（Mathematical Objects）

---

---

 

• 标量（Scalar）

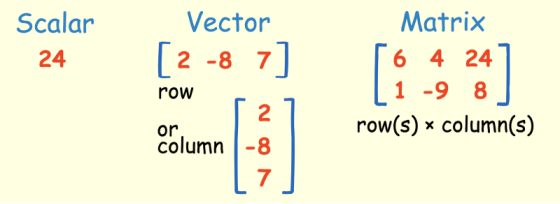
标量只是一个单一的数字。 例如24。

• 向量（Vector）

向量是一个有序的数字数组，可以在一行或一列中。 向量只有一个索引，可以指向矢量中的特定值。 例如，V2代表向量中的第二个值，在上面的黄色图片中为“-8”。

▌矩阵（Matrix）

---

---

 

矩阵是一个有序的二维数组，它有两个索引。 第一个指向行，第二个指向列。 例如，M23表示第二行和第三列中的值，在上面的黄色图片中为“8”。 矩阵可以有多个行和列。 请注意，向量也是一个矩阵，但只有一行或一列。

在黄色图片的例子中的矩阵也是2×3维的矩阵（行*列）。 下面你可以看到矩阵的另一个例子及其符号：

• 张量（Tensor）

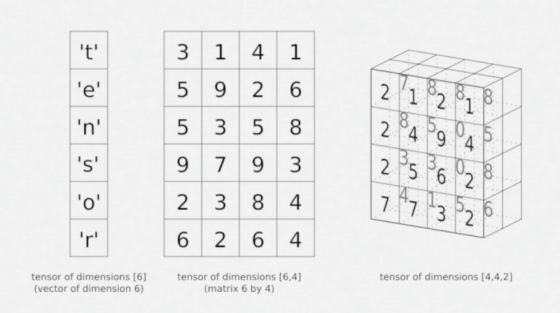
张量是一组数字，排列在一个规则的网格上，具有不同数量的轴。 张量有三个指标，第一个指向行，第二个指向列，第三个指向轴。 例如，V232指向第二行，第三列和第二个轴。 这在下图最右边张量中的值为0：

这是上述所有概念中最通用的术语，因为张量是一个多维数组，它可以是一个矢量和一个矩阵，它取决于它所具有的索引数量。 例如，一阶张量将是一个向量（1个索引）。 二阶张量是矩阵（2个指数）和三阶张量（3个指数），更高的称为高阶张量（超过3个指数）。

▌计算规则（Computational Rules）

---

---

 

• 1.矩阵标量运算（Matrix-Scalar Operations）

如果在矩阵基础上乘除或者加一个变量，就代表对矩阵的每一个元素进行数学运算。 下图显示了的乘法例子：

• 2.矩阵向量乘法（Matrix-Vector Multiplication）

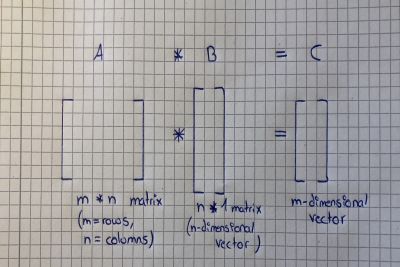
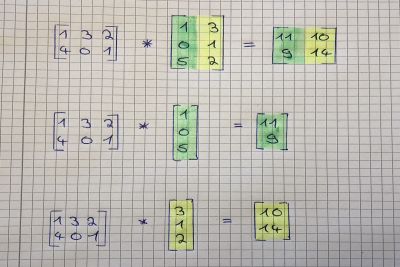
将矩阵与矢量相乘可以被认为是将矩阵的每一行与矢量的列相乘。 输出将是一个具有与矩阵相同行数的向量。 下图显示了这是如何工作的：

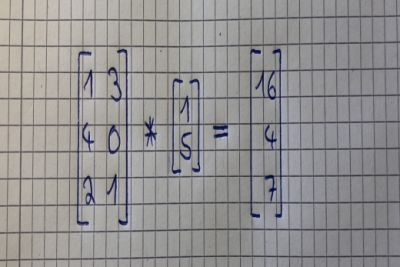
为了更好地理解这个概念，我们计算第二个图像。 为了得到结果向量的第一个值（16），我们将我们想要与矩阵（1和5）相乘的向量的数字乘以矩阵的第一行的数字（1和3））。

像这样：

1 * 1 + 3 * 5 = 16

我们对矩阵的第二行中的值也做同样的操作：

4 * 1 + 0 * 5 = 4

再次计算矩阵的第三行：

2 * 1 + 1 * 5 = 7

这是另一个例子：

下图是一个总结：

• 3.矩阵 - 矩阵加法和减法（ Matrix-Matrix Addition and Subtraction）

矩阵与矩阵加法和减法相当简单直接。 要求是矩阵具有相同的尺寸，并且结果将是具有相同尺寸的矩阵。 您只需在第一个矩阵中添加或减去第二个矩阵的每个值进行元素级的运算。如下图所示：

• 4.矩阵 - 矩阵乘法（Matrix-Matrix Multiplication）

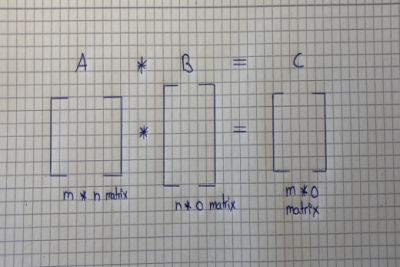
如果你知道如何将一个矩阵乘以一个向量，那么将两个矩阵相乘并不困难。 请注意，如果第一个矩阵列的数量与第二个矩阵行的数量匹配，两个矩阵才能做乘法运算。 结果将是一个与第一个矩阵相同行数和与第二个矩阵相同列数的矩阵。 它的计算方法如下：

将第二个矩阵拆分为列向量，然后将第一个矩阵分别与这些向量中的每一个相乘。 然后你把结果放在一个新的矩阵中。 下面的图片逐步解释了这一点：

下图进行总结：

▌矩阵乘法属性（Matrix Multiplication Properties）

---

---

 

矩阵乘法有几个属性，我们将在下面逐一讨论。为了更好地理解我们将首先用标量来解释这些概念，然后再运用于矩阵。

• 1.不可交换（Not Commutative）

标量乘法是可交换的，但矩阵乘法不行。这意味着当我们乘以标量时，7 * 3与3 * 7相同。但是当我们将矩阵彼此相乘时，A * B与B * A不一样。

• 2.结合律（Associative）

标量和矩阵乘法都有结合律。这意味着标量乘3（5 * 3）与（3 * 5）3相同并且矩阵乘A（B * C）与（A * B）C相同。

• 3.分配律（Distributive）

标量和矩阵乘法也是满足分配律。这意味着3（5 + 3）与3 * 5 + 3 * 3相同，并且A（B + C）与A * B + A * C相同。

• 4.单位矩阵（Identity Matrix）

单位矩阵是一种特殊的矩阵，但首先，我们需要定义什么是单位。数字1是一个单位，因为你与1相乘的所有东西都等于它自己。因此，与单位矩阵相乘的每个矩阵都等于它自己。例如，矩阵A乘以其单位矩阵等于A。

您可以通过以下事实来发现单位矩阵：它沿对角线为1，其他每个值都为零。它也是一个“方阵”，意思是它的行数与列数相同。

我们之前讨论过矩阵乘法不是可交换的，但是有一个例外，即如果我们将矩阵乘以单位矩阵。 因此，以下等式成立：A * I = I * A = A

▌反转和转置 （Inverse and Transpose）

---

---

 

矩阵逆和矩阵转置是两种特殊的矩阵属性。 再次，我们将首先讨论这些属性如何与实数相关，然后讨论它们与矩阵的关系。

• 1. 逆 （Inverse）

首先，什么是矩阵的逆？ 乘以其倒数的数字等于1.请注意，除0以外的每个数字都有倒数。 如果你将矩阵乘以它的逆，结果将是它的单位矩阵。 下面的例子展示了标量的逆：

但不是每个矩阵都有逆矩阵。 如果矩阵是“方阵”并且它可以具有逆矩阵，则可以计算矩阵的逆矩阵。 讨论哪些矩阵具有逆的情况超出了本文的范围。

为什么我们需要一个逆？ 因为我们不能除以矩阵。 没有矩阵除法的概念，但我们可以通过逆矩阵乘以矩阵，产生相同的结果。

下图显示了一个矩阵，它乘以自己的逆矩阵，得到一个2乘2的单位矩阵。

您可以使用Numpy轻松计算矩阵的逆（如果可以的话）。 下面是文档链接：

https：//docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.linalg.inv.html

• 2.转置 （Transpose）

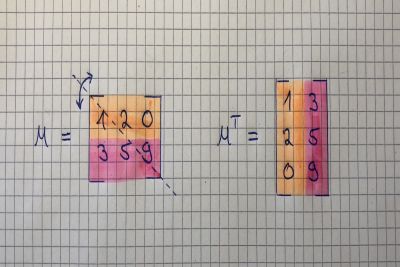
最后，我们将讨论矩阵转置。 这基本上是沿着45度轴线的矩阵的镜像。 获得矩阵的转置相当简单。 它的第一列仅仅是移调矩阵的第一行，第二列变成了矩阵移调的第二行。 一个m * n矩阵被简单地转换成一个n * m矩阵。 另外，A的Aij元素等于Aji（转置）元素。 下图说明：

▌总结

---

---

在这篇文章中，您了解了机器学习中使用的线性代数的数学对象。 你还学会了如何对这些数学对象进行乘，除，加和减操作。 此外，您已经了解了矩阵的最重要属性，以及为什么它们使我们能够进行更高效的计算。 最重要的是，你已经学会了什么是逆矩阵和转置矩阵，你可以用它做什么。 虽然在机器学习中也使用了线性代数的其他部分，但这篇文章给了你一个最重要概念的正确介绍。

参考文献

Deep Learning (book) — Ian Goodfellow, Joshua Bengio, Aaron Courville

 https://machinelearningmastery.com/linear-algebra-machine-learning/

 

Andrew Ng’s Machine Learning course on Coursera

 https://en.wikipedia.org/wiki/Linear_algebra

 https://www.mathsisfun.com/algebra/scalar-vector-matrix.html

 https://www.quantstart.com/articles/scalars-vectors-matrices-and-tensors-linear-algebra-for-deep-learning-part-1

 https://www.aplustopper.com/understanding-scalar-vector-quantities/

原文链接：

https://towardsdatascience.com/5-types-of-regression-and-their-properties-c5e1fa12d55e

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！加入专知主题群（请备注主题类型：AI、NLP、CV、 KG等）交流~

点击“阅读原文”，使用专知