博客 | MIT—线性代数(上)
本文原载于知乎专栏“AI的怎怎,歪歪不喜欢”,AI研习社经授权转载发布。欢迎关注 邹佳敏 的知乎专栏及 AI研习社博客专栏(文末可识别社区名片直达)。
社长提醒:本文的相关链接请点击文末【阅读原文】进行查看
在中国不知所以的《线性代数》教材的目录排版下,当前大多数本土毕业生均能熟练使用公式计算行列式或求解线性方程组,却丝毫不能体会线性代数真正内涵的精髓所在。包括我在内,在学习机器学习那满篇的矩阵表示更是让人头痛欲裂,这让我事实上感受到了线性代数才是机器学习中最重要的数学工具,因此不得不静下心来按照网易名校公开课—“MIT线性代数”重学一遍,受到的启发超乎想象,线性代数新世界的大门似乎也对我缓缓打开,遂有了这两篇学习笔记,供自己或有兴趣的小伙伴后续参考。
1、 方程组的几何解释:一个特定的线性方程组可以从3个角度去观察:行视图,列视图和矩阵表示。行视图为所有人熟知,即求解空间内不同方程所代表的线、面、体交点;列视图表示空间内列向量间的线性表示,在线性代数上用到最多;矩阵表示则是引入矩阵,将方程组以Ax=b重新编排,A是m*n的矩阵。从列视图角度重新理解方程组的解,即向量b是否包含在A的列空间内,或b能否用A的列向量线性表出。
2、 矩阵消元:行空间角度。使用高斯消元求解Ax=b,将A化简为行阶梯形式,等价于使用某个矩阵变换E左乘A的行向量,即E·A·x=U·x=E·b,其中E记录了高斯消元中所有的行变换,U表示行阶梯形式的消元结果,是一个上三角矩阵。其中,行变换为左乘,列变换为右乘。
3、 乘法和逆矩阵:矩阵乘法A·B=C有4种解释方式:①中文教材中介绍最多的方法,Ai行·Bj列=Cij;②A列空间·Bj列 =Cj列,即C的列向量是A列空间的线性组合;③Ai行·B行空间=Ci行,即C的行向量是B行空间的线性组合;④A列空间·B行空间=sigma(Aj列·Bi行)。如果A·B = B·A = I,则A与B互为可逆矩阵。若矩阵A可逆,则|A|不等于0,或者Ax=0只有零解。逆矩阵可以通过将[A|E]全用行变换或全用列变换为[E|B]求得。
4、 A的LU分解:前文提到使用E记录高斯消元所有步骤,即E·A=U可以对A的行空间变换得到上三角矩阵U。此时,考虑某个线性变换L,将U行重新变换回A,直观理解L就是E的逆操作,即E逆,它是一个下三角矩阵。因此,对任意一个矩阵都存在L和U使其A=L·U。
5、 置换、转置和向量空间:矩阵置换是交换A的两行。置换目的是在A的行空间变换中,若消元后的主元位置并非依次排列,就需要通过额外的置换矩阵调整之。因此,准确来说,存在置换矩阵P,使得P·A=L·U。对于任意置换矩阵, 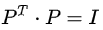
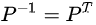
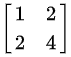
6、 列空间和零空间:A的列空间是由A矩阵列向量中最大线性无关组所构成的子空间。若无关组向量个数为r,则A的列空间即为Rm空间中的r维子空间。对A·x=b,若b位于A的列空间中,则方程组有解,否则无解。即如果m>n,即方程组方程个数大于变量个数,则A的列空间仅仅只是一个子空间,没有把Rm空间撑满,所以会存在无解的情况。倘若无关组个数r=m,则A的列空间撑满Rm,对任意向量b,均有解。A的零空间是由A·x=0的解构成的子空间,若A消元后有r个主元,则存在n-r个自由变量,则A的零空间即为Rn空间中的n-r维子空间。另外,列空间和零空间必须满足数乘和加减封闭。
7、 Ax=0主变量和特解:求解Ax=0首先要使用高斯消元将A转换为标准行阶梯矩阵U,求解Ux=0的解空间即A的零空间不变。我们称U中每一行第一个非零元素所在的列为主元,个数为r,全零行对应的列为自由变量,个数为n-r。构造自由变量为线性无关向量后回代方程组,求解对应的主元数值,所得到的n-r个线性无关解向量被称为基础解系,基础解系对应的解空间即为A的零空间。
8、 Ax=b可解性和解的结构:此时对[A|b]进行高斯消元,并化简为标准行阶梯矩阵。方程的可解性要参考m*n矩阵A与其列空间维数r之间的关系,其中r<=m且r<=n。若A列满秩r=n,则Ax=0的零空间只有零向量,Ax=b有唯一解或无解,无解时b刚好落在列空间之外,即A的全零行所对应的b不为0。若A行满秩r=m,每一行均存在一个主元,Ax=b必有解,自由变量个数为n-r,此时方程组有唯一解或无穷多解,唯一解时r=m=n。若r<m且r<n,无解或无穷多解。
9、 线性相关性、基和维数:线性无关表明不存在一组非零系数使得向量组之间可以线性表出,它是构成基的前提。基在线性无关的基础上,还要有能力构建一个子空间,它决定子空间维数。维数则是在子空间中基的个数。总而言之,若全体向量组中每个向量有m个元素,但向量组内最大线性无关组个数为r,则该最大线性无关组即为Rm空间中r维子空间的基!对矩阵A来说,其最大线性无关的列向量组是A列空间的基,维数为r;Ax=0的自由变量所构建的基础解系线性无关,是A零空间的基,维数为n-r。
10、 四个基本子空间:矩阵A的四个基本子空间中除了前文介绍的列空间和零空间外还有行空间和左零空间,这里有一个小trick就是对 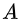
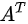
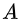
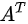
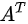
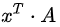
11、 矩阵空间、秩1矩阵和小世界图:向量空间中研究的对象是向量及其向量间的线性组合。而矩阵空间中的研究对象则变为矩阵,研究的是矩阵间的线性组合,同理,矩阵空间需要对数乘和加减封闭。举例来说,对3*3矩阵而言,一般矩阵的维数是9,对称矩阵的维数是6,单位矩阵的维数是3。对秩1矩阵的研究主要在于可以将任意秩为r的矩阵分解为r个秩1矩阵的乘积。两个矩阵和的秩通常小于等于两个矩阵秩的和,所以秩1矩阵本身并不能构成一个子空间,因为秩1矩阵和的秩通常发生了改变。小世界图是“六度空间假设”的理论版本。
12、 图和网络:线性代数的理论并非凭空捏造,它们来自实际问题,描述问题的拓扑结构,而线性代数通常就适合图和网络问题中的数学建模。本课结合物理电流和电路理论,从线性代数的角度证明了欧拉公式和基尔霍夫电流定律。
13、 正交向量和子空间:因为正交向量间的点积等于0,即 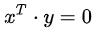
14、 子空间投影:(个人认为这是线性代数在机器学习领域最重要的知识点!)
子空间投影由Ax=b引出,它解决的问题是:若Ax=b无解,如何得到最适合Ax=b的解呢?首先,由Ax=b无解,可以知道b不属于A的列空间或b不能使用A列空间的基线性表出,这在m>n的长方形矩阵中非常常见,即A的列空间并没有把Rm撑满。因此,最优的方法就是把b投影到A的列空间中,求解Ax’=p,p是将b投影至A的列空间后的投影向量。
投影到一维子空间情形: 将b向量投影到一维子空间上,即a向量方向,假设投影后的向量 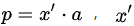
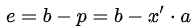
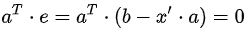
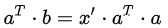
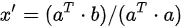
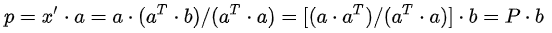
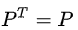
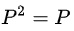
投影到二维及高维子空间情形:
将b向量投影到二维子空间上,即子空间基的方向。首先定义二维子空间的基a1,a2(A=[a1,a2]),则投影 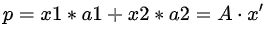
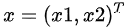
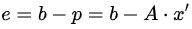
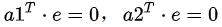
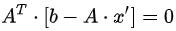
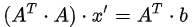
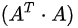
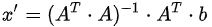
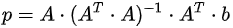
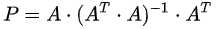
推荐阅读
【AI求职百题斩】已经悄咪咪上线啦,还不赶紧来答题?!
想知道正确答案?
回公众号聊天界面并发送“1218挑战”即可获取!
点击 阅读原文 查看本文更多内容↙