Balancing weights for region-level analysis: the effect of Medicaid Expansion on the uninsurance rate among states that did not expand Medicaid

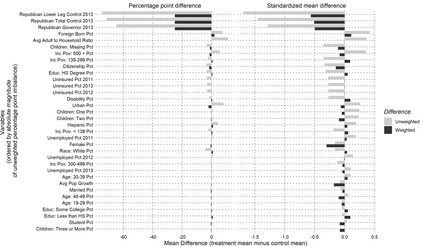
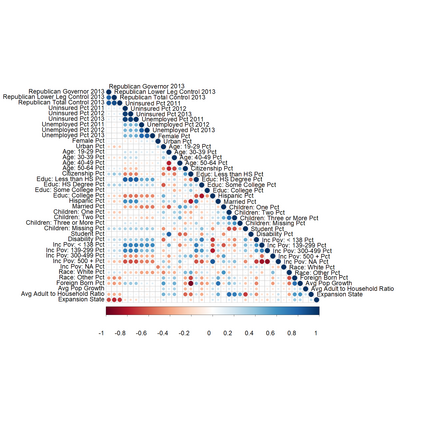
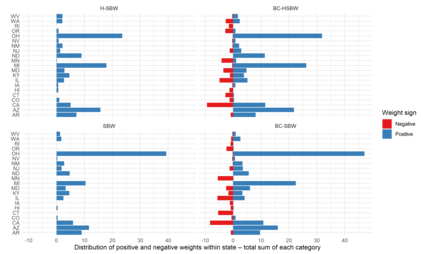
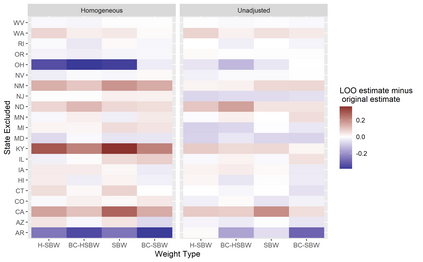
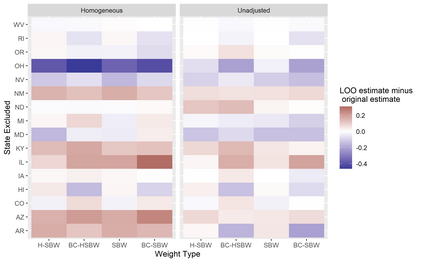
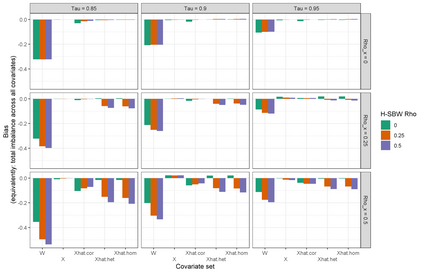
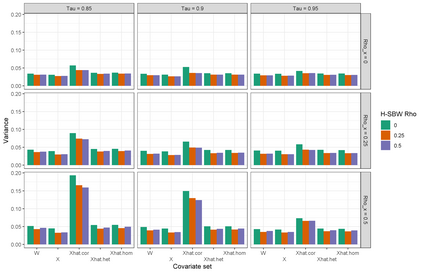
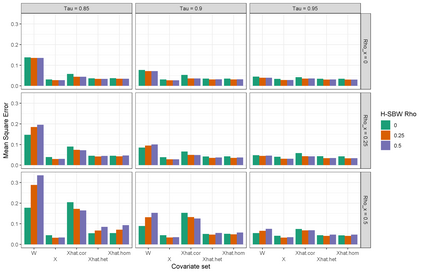
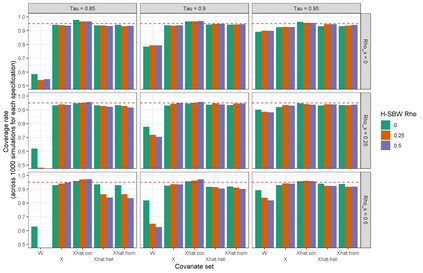
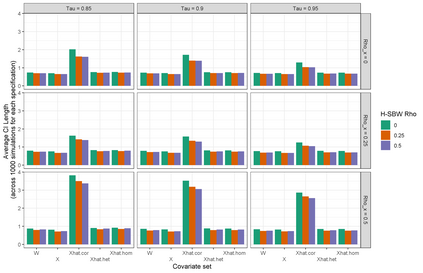
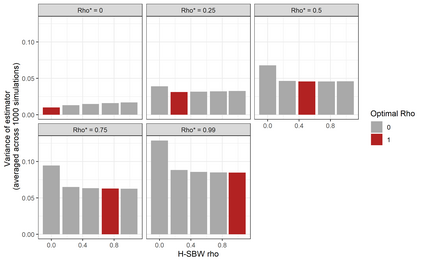
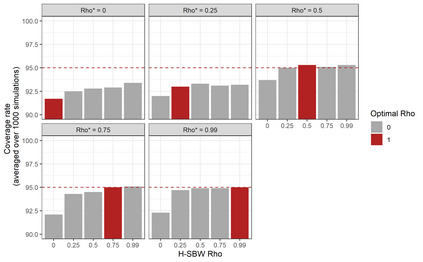
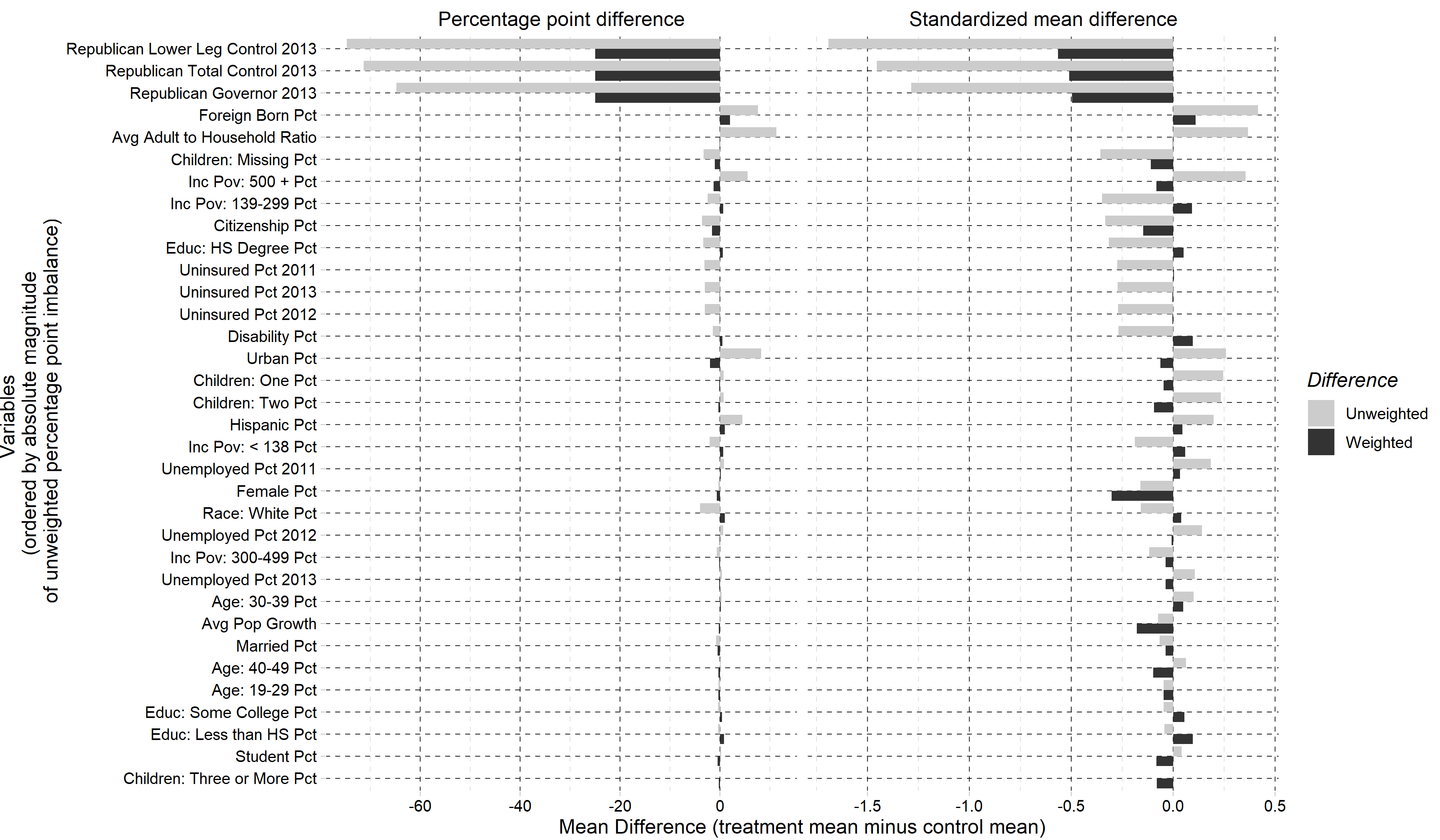
We predict the average effect of Medicaid expansion on the non-elderly adult uninsurance rate among states that did not expand Medicaid in 2014 as if they had expanded their Medicaid eligibility requirements. Using American Community Survey data aggregated to the region level, we estimate this effect by finding weights that approximately reweights the expansion regions to match the covariate distribution of the non-expansion regions. Existing methods to estimate balancing weights often assume that the covariates are measured without error and do not account for dependencies in the outcome model. Our covariates have random noise that is uncorrelated with the outcome errors and our outcome model has state-level random effects inducing dependence between regions. To correct for the bias induced by the measurement error, we propose generating our weights on a linear approximation to the true covariates, using an idea from measurement error literature known as "regression-calibration" (see, e.g., Carroll (2006)). This requires auxiliary data to estimate the variability of the measurement error. We also modify the Stable Balancing Weights objective proposed by Zubizaretta (2015)) to reduce the variance of our estimator when the model errors follow our assumed correlation structure. We show that these approaches outperform existing methods when attempting to predict observed outcomes during the pre-treatment period. Using this method we estimate that Medicaid expansion would have caused a -2.33 (-3.54, -1.11) percentage point change in the adult uninsurance rate among states that did not expand Medicaid.