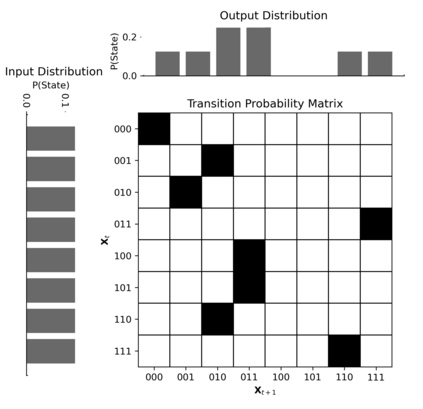
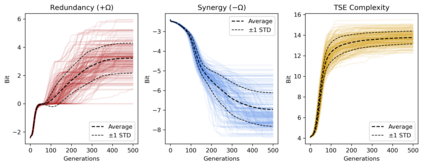
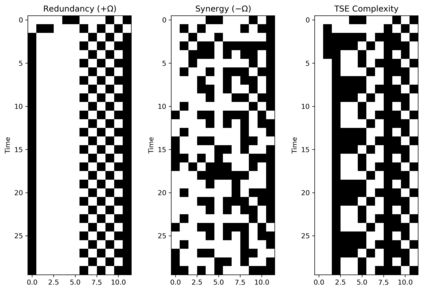
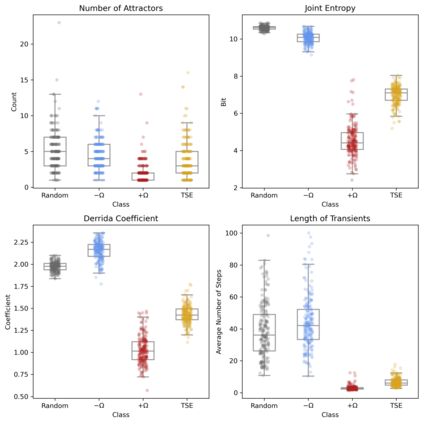
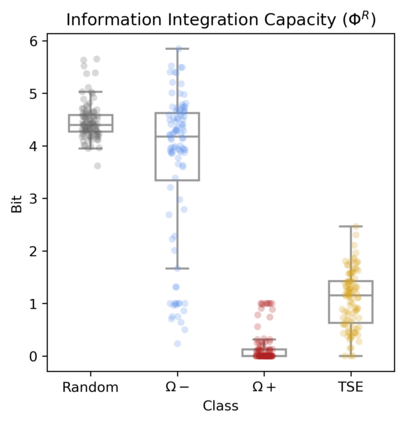
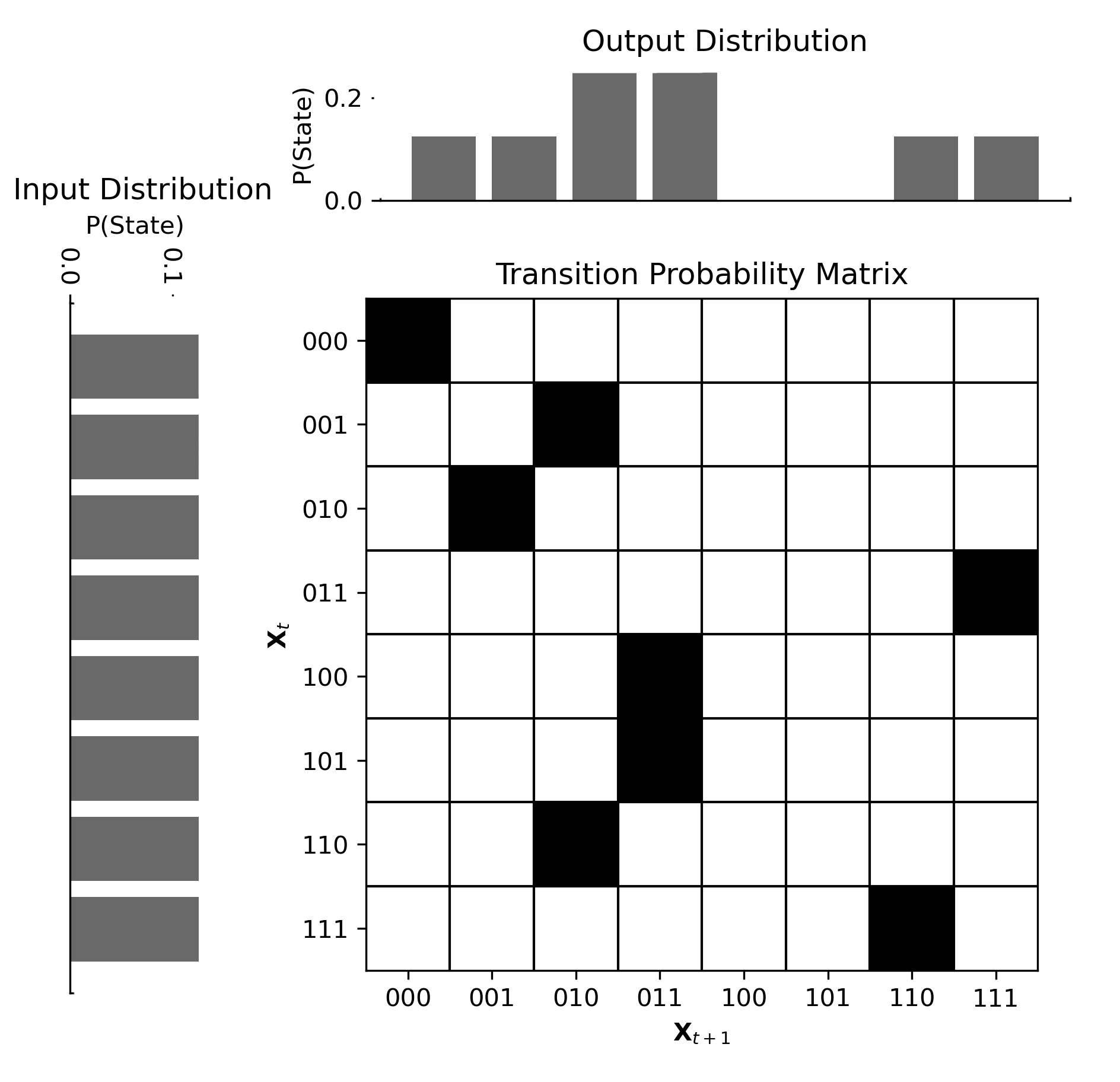
There has recently been an explosion of interest in how "higher-order" structures emerge in complex systems. This "emergent" organization has been found in a variety of natural and artificial systems, although at present the field lacks a unified understanding of what the consequences of higher-order synergies and redundancies are for systems. Typical research treat the presence (or absence) of synergistic information as a dependent variable and report changes in the level of synergy in response to some change in the system. Here, we attempt to flip the script: rather than treating higher-order information as a dependent variable, we use evolutionary optimization to evolve boolean networks with significant higher-order redundancies, synergies, or statistical complexity. We then analyse these evolved populations of networks using established tools for characterizing discrete dynamics: the number of attractors, average transient length, and Derrida coefficient. We also assess the capacity of the systems to integrate information. We find that high-synergy systems are unstable and chaotic, but with a high capacity to integrate information. In contrast, evolved redundant systems are extremely stable, but have negligible capacity to integrate information. Finally, the complex systems that balance integration and segregation (known as Tononi-Sporns-Edelman complexity) show features of both chaosticity and stability, with a greater capacity to integrate information than the redundant systems while being more stable than the random and synergistic systems. We conclude that there may be a fundamental trade-off between the robustness of a systems dynamics and its capacity to integrate information (which inherently requires flexibility and sensitivity), and that certain kinds of complexity naturally balance this trade-off.
翻译:暂无翻译