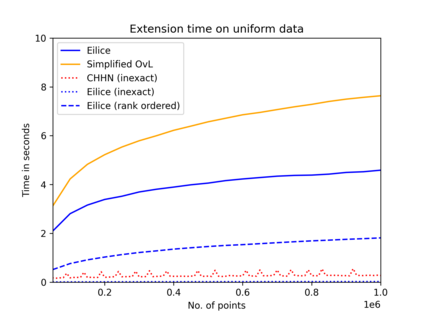
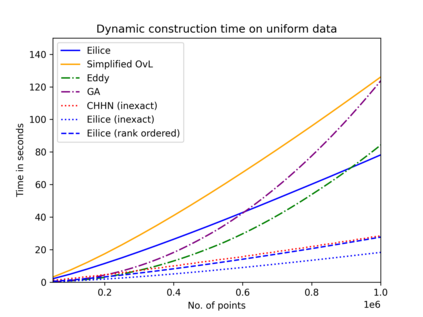
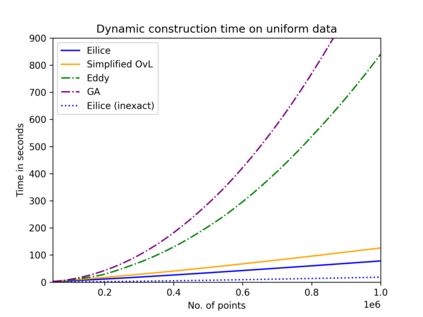
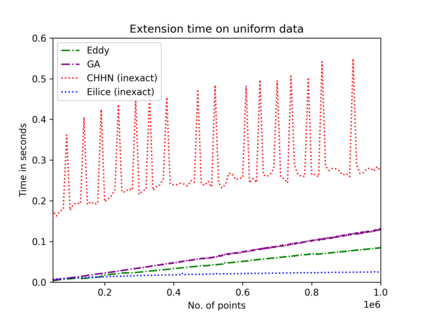
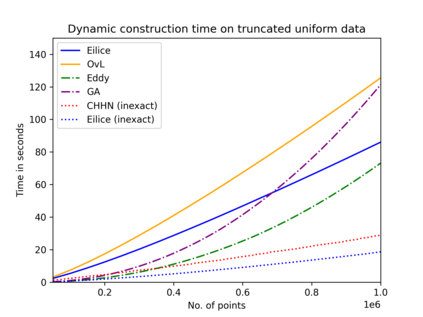
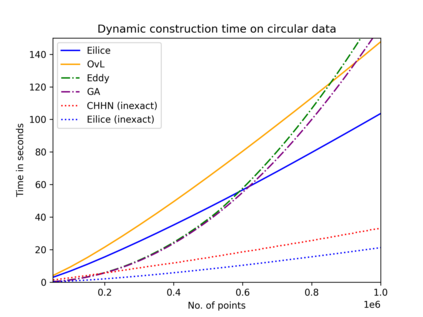
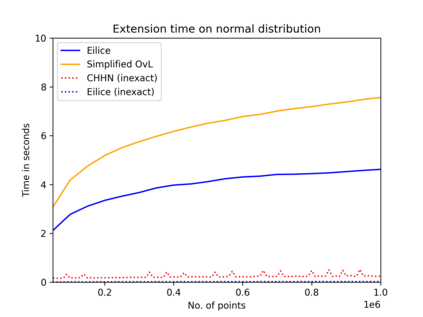
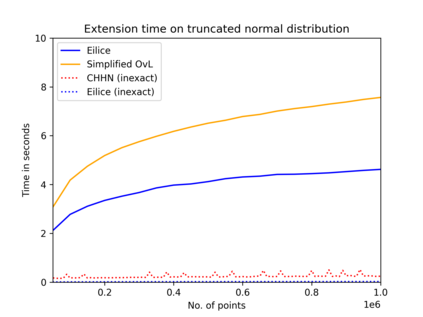
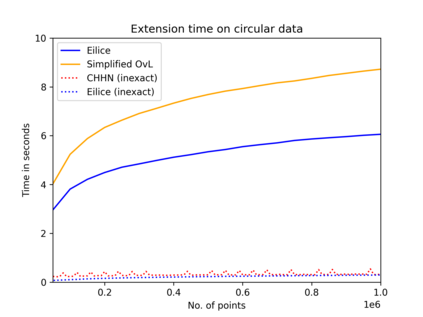
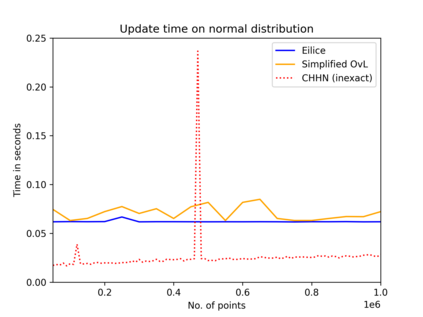
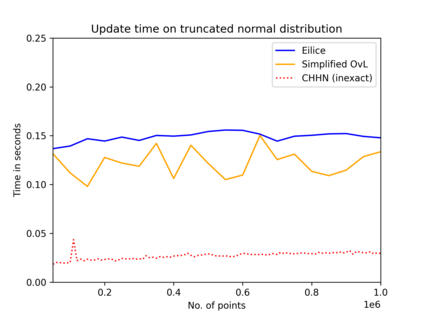
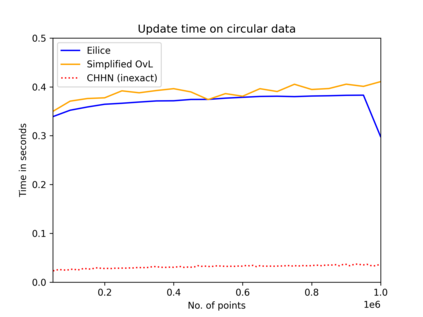
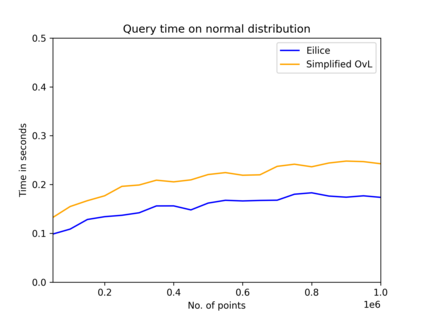
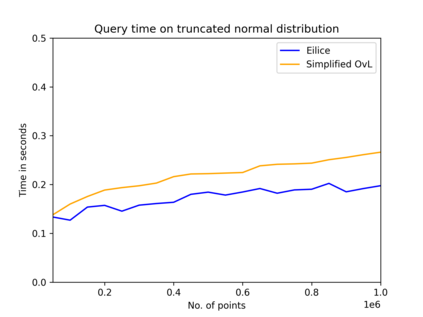
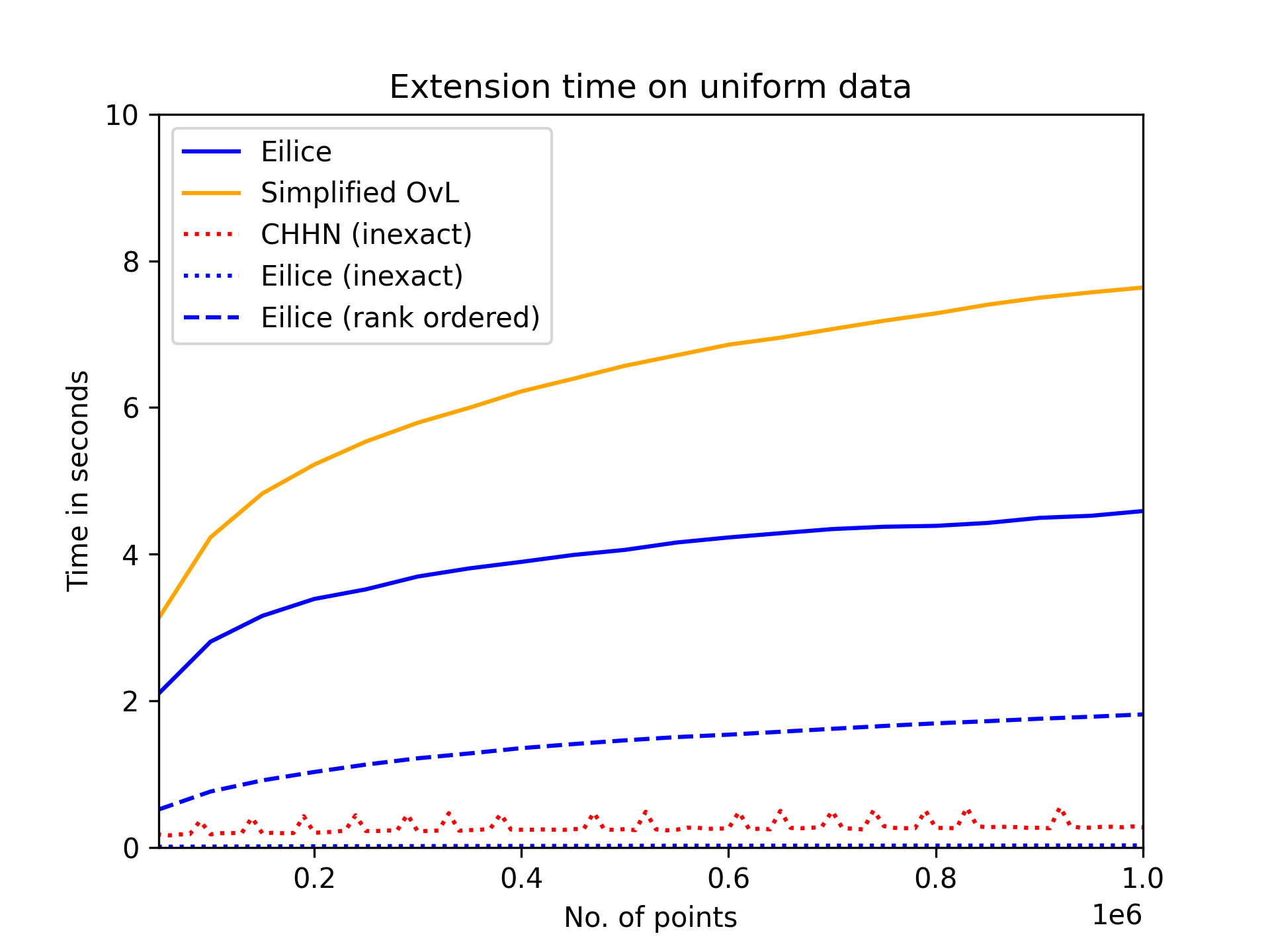
The convex hull of a data set $P$ is the smallest convex set that contains $P$. In this work, we present a new data structure for convex hull, that allows for efficient dynamic updates. In a dynamic convex hull implementation, the following traits are desirable: (1) algorithms for efficiently answering queries as to whether a specified point is inside or outside the hull, (2) adhering to geometric robustness, and (3) algorithmic simplicity.Furthermore, a specific but well-motivated type of two-dimensional data is rank-based data. Here, the input is a set of real-valued numbers $Y$ where for any number $y\in Y$ its rank is its index in $Y$'s sorted order. Each value in $Y$ can be mapped to a point $(rank, value)$ to obtain a two-dimensional point set. In this work, we give an efficient, geometrically robust, dynamic convex hull algorithm, that facilitates queries to whether a point is internal. Furthermore, our construction can be used to efficiently update the convex hull of rank-ordered data, when the real-valued point set is subject to insertions and deletions. Our improved solution is based on an algorithmic simplification of the classical convex hull data structure by Overmars and van Leeuwen~[STOC'80], combined with new algorithmic insights. Our theoretical guarantees on the update time match those of Overmars and van Leeuwen, namely $O(\log^2 |P|)$, while we allow a wider range of functionalities (including rank-based data). Our algorithmic simplification includes simplifying an 11-case check down to a 3-case check that can be written in 20 lines of easily readable C-code. We extend our solution to provide a trade-off between theoretical guarantees and the practical performance of our algorithm. We test and compare our solutions extensively on inputs that were generated randomly or adversarially, including benchmarking datasets from the literature.
翻译:暂无翻译