Clearing Payments in Dynamic Financial Networks

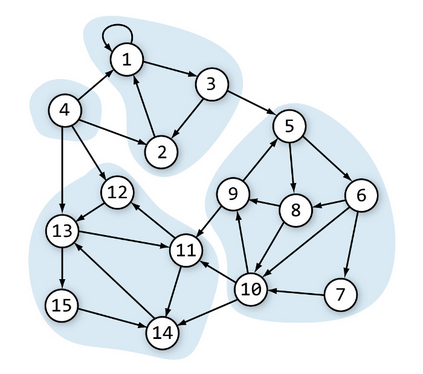
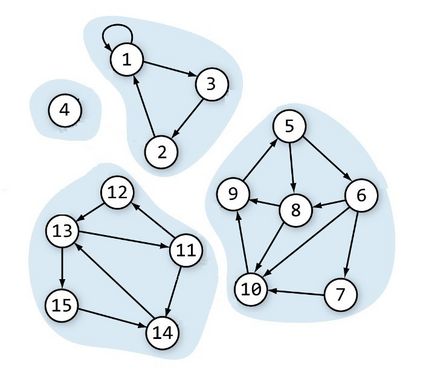
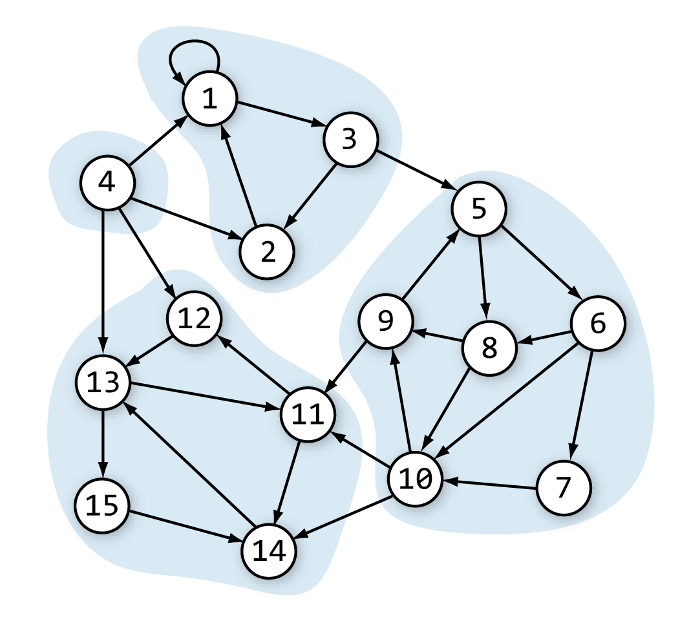
In this paper, we propose a novel dynamical model of clearing in a financial network, which stems from the classical Eisenberg- Noe model of financial contagion. The Eisenberg-Noe model assumes that at one point in time (say, at the end of a day), all liabilities are claimed and due simultaneously, and that the entire network of banks becomes aware of the claims and possible defaults and instantaneously agrees on the clearing payments. The motivation for the dynamic model we propose in this paper is that one may expect that if financial operations are allowed for a given number of time periods after the initial theoretical defaults, some nodes may actually recover and eventually manage to fulfill their obligations. We prove that the proposed model obeys the standard requirement known as the priority of debt claims, that is, each node either pays its liabilities in full, or it pays out all its balance. We also show that the requirements of ro-rata payments determines the solution uniquely.