教程题目
知识图主要思想简史教程:A Brief History of Knowledge Graph's Main Ideas: A tutorial
教程内容
知识图谱可以被认为是实现了计算机科学早期的愿景,即创建大规模集成知识和数据的智能系统。“知识图”一词是在本世纪初由研究人员提出的,自2012年谷歌推广以来,在学术界和业界迅速流行起来。必须指出的是,无论“知识图”一词的讨论和定义如何,它都源于语义网、数据库、知识表示和推理、自然语言处理、机器学习等不同研究领域的科学进步。来自这些不同学科的思想和技术的集成使知识图的概念更加丰富,但同时也给实践者和研究者提出了一个挑战,使他们知道当前的进步是如何从早期技术发展而来的,并植根于早期技术。
教程作者
Claudio Gutierrez ,Juan F. Sequeda,来自于智利国立大学。
成为VIP会员查看完整内容
相关内容
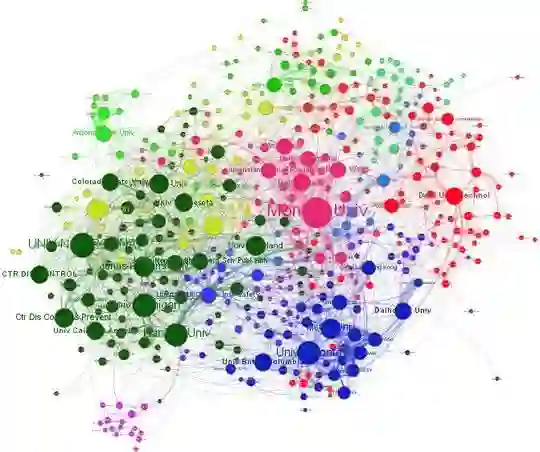
知识图谱(Knowledge Graph),在图书情报界称为知识域可视化或知识领域映射地图,是显示知识发展进程与结构关系的一系列各种不同的图形,用可视化技术描述知识资源及其载体,挖掘、分析、构建、绘制和显示知识及它们之间的相互联系。
知识图谱是通过将应用数学、图形学、信息可视化技术、信息科学等学科的理论与方法与计量学引文分析、共现分析等方法结合,并利用可视化的图谱形象地展示学科的核心结构、发展历史、前沿领域以及整体知识架构达到多学科融合目的的现代理论。它能为学科研究提供切实的、有价值的参考。
专知会员服务
207+阅读 · 2020年2月16日
Arxiv
5+阅读 · 2019年1月29日