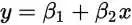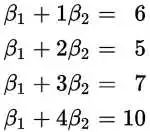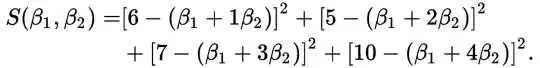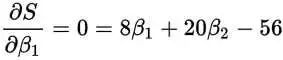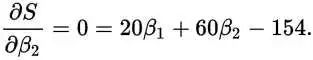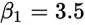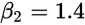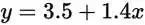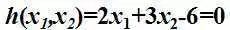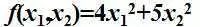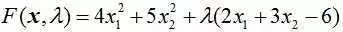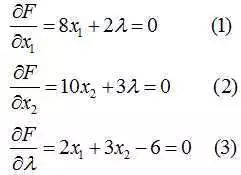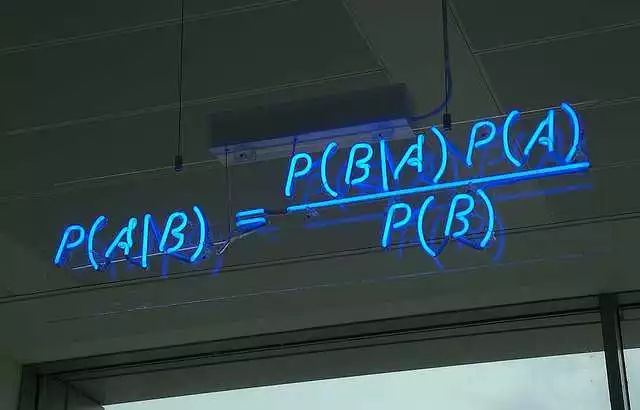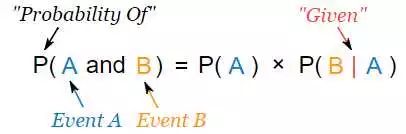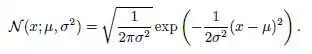机器学习应该准备哪些数学预备知识？

2017 年 11 月 26 日 AI100 Jacky Yang

作者 | Jacky Yang

本文授权转自Jacky Yang的知乎专栏

最近在给几位程序员朋友培训机器（深度）学习，而且10月份刚把数学基础部分培训完，看到这个问题，结合培训的感受，趁热写一点小小的心得体会。

看了一下题主的问题，的确，现在很多想从事于机器学习的朋友都存在类似的困惑，主要是很多相关的书看不懂，尤其是数学部分，包括题主提到的PRML，还有最近的深度学习圣经。不得不说，这些书籍其实都很经典，但经典的书未必都适合每个人，毕竟这些著作其实是有一些门槛的，所以如何把这个门槛降低，或者换一个说法，如何把其中的数学基础用通俗易懂的语言解读出来，也是很有意义的一件事。我在培训当中也是深有体会。

以下我假定读者跟题主情况类似：希望从事于机器学习，但数学多年不用，在阅读算法书籍的过程中，数学部分理解起来有难度。

同时也欢迎业内朋友提供宝贵建议和意见。

对于绝大多数从事于机器学习的人来说，学数学的目的，主要是便于（深入）理解算法的思路。那么问题来了，我们到底要把数学学到什么程度？

我这里举几个例子：

1. 线性最小二乘法

大家可以随意搜索一下，相关的文章很多。长篇大论的不少，刚入门的朋友一看到那些公式可能就看不下去了。比如下面的解释：

毫无疑问，这样的解释是专业的，严谨的。事实上，这是深度学习圣经里的解释。我并没有诋毁大师的意思，只是觉得用一个具体的例子来说明，可能会让读者更加容易理解：

小明是跑运输的，跑1公里需要6块，跑2公里需要5块（那段时间刚好油价跌了），跑3公里需要7块，跑4公里需要10块，请问跑5公里需要多少块？

如果我们有初中数学基础，应该会自然而然地想到用线性方程组来做，对吧。

这里假定x是公里数，y是运输成本（β1和β2是要求的系数）。我们把上面的一组数据代入得到这么几个方程：

如果存在这样的β1和β2，让所有的数据（x，y）=（1,6），（2,5），（3,7），（4，10）都能满足的话，那么解答就很简单了，β1+5β2就是5公里的成本，对吧。

但遗憾的是，这样的β1和β2是不存在的，上面的方程组很容易，你可以把前面两个解出来得到一组β1和β2，后面两个也解出来同样得到一组β1和β2。这两组β1和β2是不一样的。

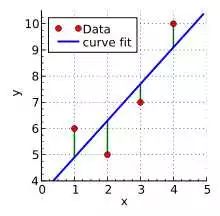
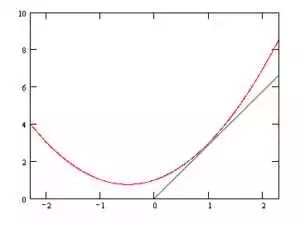
形象地说，就是你找不到一条直线，穿过所有的点，因为他们不在一条直线上。如下图：

可是现实生活中，我们就希望能找到一条直线，虽然不能满足所有条件，但能近似地表示这个趋势，或者说，能近似地知道5公里的运输成本，这也是有意义的。

现实生活当中，有很多这样的例子，想起以前在某公司上班的时候，CEO说我们研发部做事有个问题：一个研发任务，要求三个月做完，因为周期太短，完成不了，就干脆不做，这显然是不对的，要尽全力，哪怕三个月完成了80%，或者最终4个月完成，总比不作为的好。

其实最小二乘法也是这样，要尽全力让这条直线最接近这些点，那么问题来了，怎么才叫做最接近呢？直觉告诉我们，这条直线在所有数据点中间穿过，让这些点到这条直线的误差之和越小越好。这里我们用方差来算更客观。也就是说，把每个点到直线的误差平方加起来：

（如果上面的四个方程都能满足，那么S的值显然为0，这是最完美的，但如果做不到完美，我们就让这个S越小越好）

接下来的问题就是，如何让这个S变得最小。这里有一个概念，就是求偏导数。这里我想提一下，在培训的过程中，我发现机器学习的数学基础课程当中，微积分是大家印象最深刻的，而且也最容易理解：比如导数就是求变化率，而偏导数则是当变量超过一个的时候，对其中一个变量求变化率。如果这个概念也忘了，可以参考我在深度学习回答里那个王小二卖猪的例子。这里就不细讲了，可参考：

Jacky Yang：深度学习如何入门？

https://www.zhihu.com/question/26006703/answer/129209540

要让S取得最小值（或最大值，但显然这个函数没有最大值，自己琢磨一下），那么S对于β1和β2分别求偏导结果为0，用一个直观的图来表示：

我们看到这条曲线，前半部分是呈下降的趋势，也就是变化率（导数）为负的，后半部分呈上升的趋势，也就是变化率（导数）为正，那么分界点的导数为0，也就是取得最小值的地方。这是一个变量的情况，对于多个变量的情况，要让S取得最小值，那最好是对β1和β2分别求导（对β1求导的时候，把β2当常量所以叫求偏导），值为0：

看到这个我们就熟悉了，两个变量，刚好有两个方程式，初中学过，那么很容易得出：

其实也就意味着

这个函数也就是我们要的直线，这条直线虽然不能把那些点串起来，但它能最大程度上接近这些点。也就是说5公里的时候，成本为3.5+1.4x5=10.5块，虽然不完美，但是很接近实际情况。

在培训的过程中，一直在思考一个问题，也就是上面提到的那个，机器学习到底要把数学掌握到什么程度？首先我们得搞清楚我们到底要拿机器学习干什么，机器学习本来就是要通过分析现实生活中的数据得出其中的规律，以便为将来各方面提供指导意义。既然是这样，为何不直接从现实中来到现实中去，直接用数据和案例来讲解数学呢。我们显然不是为了学数学才学的机器学习，那就没必要堆砌哪些晦涩的公式了。除非我们要做纯理论研究。

当然，数学的一些理念，思想或者精髓是需要掌握的，其实很多时候，我们都是在做不到完美的情况下，求那个最接近完美的解，别忘了机器学习很多情况下其实是在做拟合，所以说最小二乘法对于机器学习非常重要，这也是我把它当做第一个例子的原因。其实深度学习里的反向传播不也是一样么？刚开始不完美，但我要想办法让它越来越接近完美，预测值与实际值差距越来越小。所谓训练，其实也就是不断追求完美的一个过程。

2. 拉格朗日乘子法

听到拉格朗日乘子法这个名字的时候，很多人的第一反应是：这玩意儿是不是很高深啊，先入为主地有了畏难的情绪。但我把它讲完以后，大部分人表示并不难，而且现实生活中，我们经常潜移默化会用到拉格朗日乘子法。甚至可以说，不用拉格朗日乘子法的人生都是不完整的人生。

我们来看一下定义：

虽然这个定义应该说是很简洁明了的，但对于大部分人来说，依然还是有点懵。不太清楚为什么要这么做。拉格朗日到底要搞什么飞机？

我们还是举个例子：某工厂在生产过程中用到两类原材料，其中一种单价为2万/公斤，另一种为3万/公斤，而工厂每个月预算刚好是6万。就像下面的公式：

经过分析，工厂的产量f跟两种原材料（x1，x2）具有如下关系（我们暂且不管它是如何来的，而且假定产品可以按任意比例生产）：

请问该工厂每个月最少能生产多少？

其实现实生活中我们会经常遇到类似的问题：在某个或某几个限制条件存在的情况下，求另一个函数的极值（极大或极小值）。就好比你要在北京买房，肯定不是想买什么房子就买什么房子，想买多大就买多大，而是跟你手头的金额，是否有北京户口，纳税有没有满五年，家庭开支/负担重不重，工作单位稳不稳定都有关系。

回到工厂的例子，其实就是求函数f的极值。上面我们提到，极值点可以通过求偏导（变化率为0的地方为极值点）来实现，函数f（x1，x2）对x1，x2分别求偏导，那么得出的结论是：x1，x2都为0的时候最小，单独看这个函数，这个结论对的，很显然这个函数的最小值是0（任何数的平方都是大于或等于0），而且只有x1和x2同时为0的时候，取得最小值。但问题是它不满足上面的限制条件。

怎么办呢？拉格朗日想到了一个很妙的办法，既然h（x1，x2）为0，那函数f（x1，x2）是否可以加上这个h（x1，x2）再乘以一个系数呢？任何数乘以0当然是0，f（x1，x2）加上0当然保持不变。所以其实就可以等同于求下面这个函数的极值：

我们对x1，x2以及λ分别求偏导（极值点就是偏导数均为0的点）：

解上面的方程组得到x1=1.071，x2=1.286 然后代入f（x1，x2）即可。

这里为什么要多加一个乘子λ呢，试想一下，如果λ是个固定的数（比如-1），我们也能通过上面的方程式1,2求解得到x1，x2，但是我们就得不到方程式3，其实也就是没有约束条件了。所以看到没有，拉格朗日很聪明，他希望我们在求偏导（极值点）以后，还能保留原有的约束条件。我们上面提到，单独对函数求极值不能保证满足约束条件，拉格朗日这么一搞，就能把约束条件带进来，跟求其他变量的偏导结果放在一起，既能满足约束条件，又能保证是约束条件下的极值。借用金星的一句话：完美！

当然这是一个约束条件的情况，如果有多个约束条件呢？那就要用多个不同的λ（想想为什么），正如最上面的那个定义那样，把这些加起来（这些0加起来也是0）。

机器学习里的数学，我感觉只需要掌握里面这个核心思想即可，就像拉格朗日乘子法，求条件极值---》转化为求（函数+条件）的极值，每一步都很妙。其实我想说的是，体会这种妙处以后，再看SVM的算法，会感觉舒服很多，数学主要是为了让人更好地理解算法，并不是为了数学而学数学。人生苦短，还成天被晦涩的书籍所困扰，“感觉身体好像被掏空”，这样真的好么？

3.朴素贝叶斯

之所以把这个拎出来，是因为我一直想吐槽一下那个公式：

我想吐槽，是因为几乎没有一篇文章解释这个公式是怎么来的。很多文章一上来就是这个公式。对于已经对条件概率没多少概念的朋友来说，脑子里其实一直有疑问。其实要解释并不难，把P(B)放到左边，除法改成乘法就容易理解多了。

P(A|B) x P（B） = P(B|A) x P（A）

也就是：B发生的概率 x B已经发生的情况下A发生的概率 = A发生的概率 x A已经发生的情况下B发生的概率。

如果这个不好理解，我们还是举个例子：

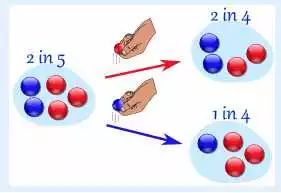
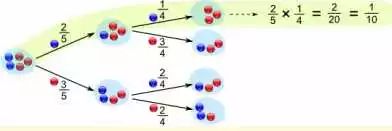
如上图所示，口袋里有5个球（2个蓝色，3个红色），每次取一个，可能的结果如下图所示：

第一次取出来是蓝色球的概率是2/5，我们把这个概率叫P(A)，然后在A发生的情况下，再取出一个红球的概率是多少？显然是3/4，因为只剩下3个红球一个蓝球，这个3/4就是P(B|A)，也就是在A发生的情况下，B发生的概率，这叫条件概率。我们把他们相乘得到：

（2/5） x （3/4）=3/10

接着我们换另一个方式算：如果第一次取到红球，第二次取到蓝球。同理，P(B)为3/5，P(A|B)为2/4，两个相乘：（3/5） x （2/4）=3/10

他们是相等的。也就是说：P(A|B) x P（B） = P(B|A) x P（A）

这个并不是特例，看下面的公式：

事实上，P(A and B) 和P(B and A)是一样的，只是一前一后发生的顺序不同。

我们把这个公式P(A|B) x P（B） = P(B|A) x P（A）的P(B)拿到另一边，这就是朴素贝叶斯的公式。

除了上面几个例子，其实还有很多方面，都可以用不那么晦涩的方式去解读。比如高斯分布，很多文章，包括一些经典书籍，一上来就是那个公式：

然而很多人并不太明白，为何要用这样的分布，为什么叫正态分布，而不叫变态分布。其实它是大自然的一种普遍规律。

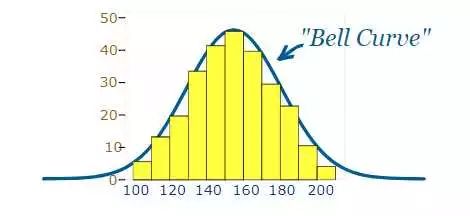
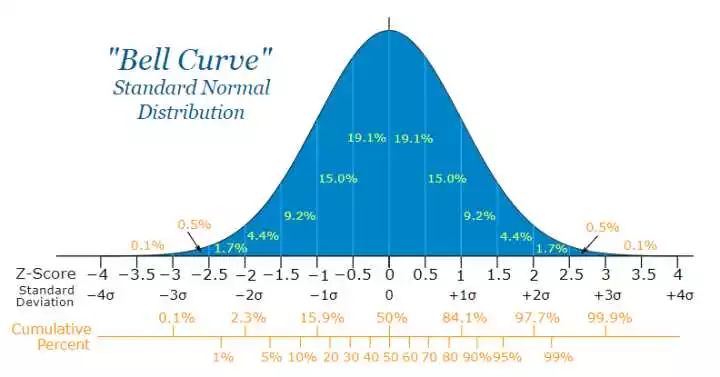
其实可以用这个图：

这是统计学生两门学习成绩总和（总分200分），横轴是分数，纵轴是所占的比例。我们发现，学霸和学渣都比较少，大部分人都集中在150分左右（很显然，大部分人都是你我这种普通人嘛），如果统计样本足够大，以至于达到无穷，那就变成了钟形曲线。普通人的平均分数，就是高斯分布里的那个μ，也就是均值，而那个σ怎么解释呢？就是你这个曲线越陡，σ越小，这个叫方差。试想一下，如果大家都挤成一坨，成绩都差不多，差别小，也就是方差小，中间的方块占的比例就越高，当然就越陡了。如下图：

另外，还有一些概念，比如正交，很多朋友问起过这个问题：Jacky，向量正交的概念我在大学里学过，但就是不知道为啥要正交？

其实我们要理解正交，可以先理解什么是相交，两条直线相交表明存在一定的夹角，但这个夹角可大可小，如果是0的情况下，他们是在一条线上的（向量都是过原点的，这里我们不考虑不过原点的情况），180度的时候也是在一条直线上，这个两种情况我们都可以认为他们是线性相关的，那么什么时候，最不相关呢，很显然是90度的时候，也就是垂直的时候。除了垂直和平行的情况，夹角在0-90度或者90度到180度之间的情况，相关性介于垂直和平行之间。

我们试想一下，如果我们要把一组数据分解成不同的特征，我们希望每个分量各自具有独立的特点呢？还是希望每个分量，你中有我，我中有你好呢？显然是越无关越好，如果他们之间太“暧昧”，就没有特点了。最好是各个分量，两两互相垂直。当然，垂直是几何上的解释，对于向量来说，更严谨的说法（多维）就是正交。

关于机器学习中数学的通俗化表达，限于篇幅（太长看了也累），先聊到这里，目前还在继续整理当中，想到哪说到哪，思路还不够清晰，希望在本次培训结束以后，能整理出一个完整的版本。同时也请业内朋友多提宝贵意见和建议。

如果在阅读PRML和deep learning的过程中，对有些数学部分不太清楚，也请在评论区留言或者私信给我也可以。请列出具体的内容或对应的书的页数。最近在写一本小册子，也很希望收到朋友们的需求，痛点及反馈。谢谢。

关于数学基础课程列表，几个高票答案总结的很全了，这里我就不重复贴了。不过有人总结了一份文档，里面列出了机器学习中用到的数学基础，虽然没有详细描述，但思路清晰，简洁明了，可以参考：

http://www.cogsci.ucsd.edu/~ajyu/Teaching/Cogs118A_wi10/Refs/basic_math.pdf