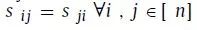图嵌入（Graph embedding）综述

会员服务 ·

图嵌入（Graph embedding）综述

2019 年 4 月 30 日 人工智能前沿讲习班

最近在学习Embedding相关的知识的时候看到了一篇关于图嵌入的综述，觉得写的不错便把文章中的一部分翻译了出来。

一、图嵌入概述

二、图嵌入的挑战

三、图嵌入的方法

一、图嵌入概述

图，如社交网络、单词共存网络和通信网络，广泛地存在于各种现实应用中。通过对它们的分析，我们可以深入了解社会结构、语言和不同的交流模式，因此图一直是学界研究的热点。图分析任务可以大致抽象为以下四类: ( a )节点分类，( b )链接预测，( c )聚类，以及( d )可视化。其中，节点分类旨在基于其他标记的节点和网络拓扑来确定节点的标签(也称为顶点)。链路预测是指预测缺失链路或未来可能出现的链路的任务。聚类用于发现相似节点的子集，并将它们分组在一起；最后，可视化有助于深入了解网络结构。

真实的图（网络）往往是高维、难以处理的，20世纪初，研究人员发明了图形嵌入算法，作为降维技术的一部分。他们首先根据实际问题构造一个D维空间中的图，然后将图的节点嵌入到d（d<<D）维向量空间中。嵌入的思想是在向量空间中保持连接的节点彼此靠近。拉普拉斯特征映射（Laplacian Eigenmaps）和局部线性嵌入（Locally Linear Embedding ，LLE）是基于这一原理的算法的例子。然而，可伸缩性是这种方法的一个主要问题，它的时间复杂度是O (| V| 2)。

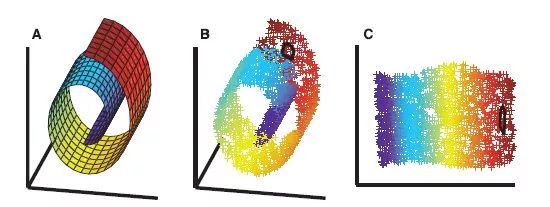
自2010年以来，关于图嵌入的研究已经转移到解决网络稀疏性的可伸缩图嵌入技术上。例如，图分解（Graph Factorization）使用邻接矩阵的近似分解作为嵌入。LINE扩展了这种方法，并试图保持一阶和二阶近似。HOPE通过使用广义奇异值分解( SVD )分解相似性矩阵而不是邻接矩阵来扩展LINE以试图保持高阶邻近性。SDNE 使用自动编码器嵌入图形节点并捕捉高度非线性的依赖关系。这些新的可扩展方法的时间复杂度为0 ( | E | )。

二、图嵌入的挑战

如前所述，图嵌入的目标是发现高维图的低维向量表示，而获取图中每个节点的向量表示是十分困难的，并且具有几个挑战，这些挑战一直在推动本领域的研究：

属性选择：节点的“良好”向量表示应保留图的结构和单个节点之间的连接。第一个挑战是选择嵌入应该保留的图形属性。考虑到图中所定义的距离度量和属性过多，这种选择可能很困难，性能可能取决于实际的应用场景。
可扩展性：大多数真实网络都很大，包含大量节点和边。嵌入方法应具有可扩展性，能够处理大型图。定义一个可扩展的模型具有挑战性，尤其是当该模型旨在保持网络的全局属性时。
嵌入的维数：实际嵌入时很难找到表示的最佳维数。例如，较高的维数可能会提高重建精度，但具有较高的时间和空间复杂性。较低的维度虽然时间、空间复杂度低，但无疑会损失很多图中原有的信息。

三、图嵌入的方法

在过去的十年里，在图形嵌入领域已经有了大量的研究，重点是设计新的嵌入算法。发展到现在，大体上可以将这些嵌入方法分为三大类：( 1 )基于因子分解的方法，( 2 )基于随机游走的方法，以及( 3 )基于深度学习的方法。在下文中我将简要解释每一个类别的特征与每一类别代表性算法的原理。

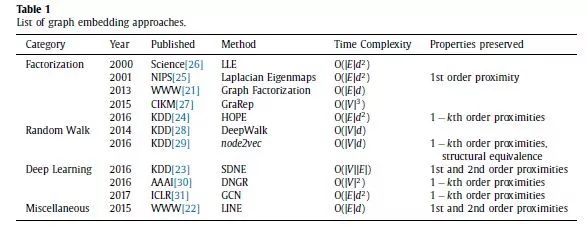
1.预备知识与符号定义

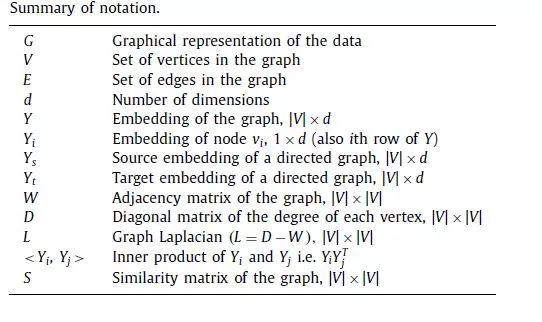
定义1 图：一个图G(V,E)由顶点集V={v1,…,vn}与边集

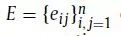
构成，图的邻接矩阵S则由每条边的权值

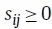
构成。如果顶点vi和vj之间没有边连接，那么

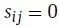
。如果图是无向图，则

。

边的权值Sij表示vi和vj的相似度，由特定的评价函数得出，值越高则两个顶点越相似。

定义2 一阶近似：边缘权重也被称为节点vi和vj之间的一阶近似值，因为它们是两个节点之间第一个也是最重要的相似性度量。

定义3 二阶近似：一对节点之间的二阶近似描述了该对节点邻域结构的相似性。设

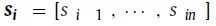
表示vi和其他节点之间的一阶接近。然后，根据si和sj的相似性确定vi和vj之间的二阶近似。二阶近似比较两个节点的邻域，如果它们具有相似的邻域，则将它们视为相似的。

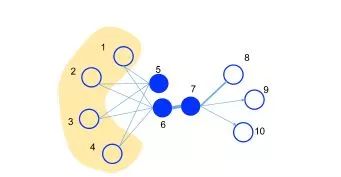
在上图中因为6和7之间有边连接，所以6和7一阶近似。5和6之间虽然没有边，但是它们有4个相同的邻居节点，所以5和6二阶近似。

定义4 图形嵌入：对于图G=（v，e），图嵌入是图的顶点的映射

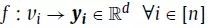
，d<<|v|,函数f保留了图G上定义的一些相似度。因此，嵌入会将每个节点映射到低维特征向量，并尝试保留顶点之间的连接强度。例如，嵌入保留一阶近似可通过最小化

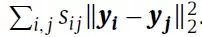
来获得接近。让两个节点对( vi，vj )和( vi，vk )与连接强度相关联，假如Sij>Sik。在这种情况下，vj将被映射到嵌入空间中比vk的映射更接近vi的点。

2.基于因子分解的方法

2.1 Locally Linear Embedding (LLE)

LLE假设每个节点都是嵌入空间中相邻节点的线性组合。如果假设图G的邻接矩阵元素代表节点j能够表示节点i的权重，我们定义

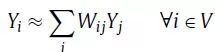
于是我们可以通过最小化

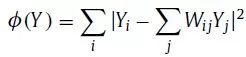
来求解嵌入后的图

。

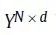
为了去除退化解，嵌入的方差被约束为

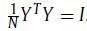
，考虑到平移不变性，嵌入以零为中心：

。

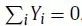
上述约束优化问题可以简化为特征值问题，其解是取稀疏矩阵

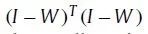
的底部d+1特征向量，并丢弃与最小特征值对应的那个特征向量。

2.2 Laplacian Eigenmaps

拉普拉斯特征映射的目的是在权重w ij较高时，保持两个节点嵌入后离得很近，也就是说被分割太远的两个相似节点会得到更多的反馈（惩罚）。具体来说，它最小化了以下目标函数：

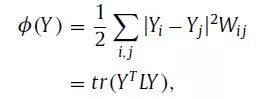
其中L是图G的拉普拉斯算子，目标函数受到

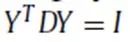
约束，以消除琐碎的解。这一问题的解可以通过取正则化L的最小的d个特征值对应的特征向量得到，

。

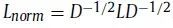
2.3. Cauchy graph embedding

拉普拉斯特征映射对嵌入节点之间的距离使用二次方的惩罚函数（

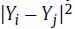
）。因此，在保持节点之间的相似性的同时，节点之间的差异性会被破坏。柯西图嵌入通过使用

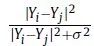
替换二次函数

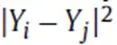
来解决这个问题，重新排列后，要最大化的目标函数变成

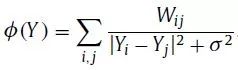
，伴随着

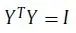
和

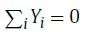
两个约束。新的目标函数是距离的反函数，因此更加强调相似的节点而不是不同的节点。

2.4. Structure Preserving Embedding (SPE)

Structure Preserving Embedding (SPE)是另一种扩展拉普拉斯特征映射的方法。SPE的目标是精确地重建输入图。嵌入被存储为一个正的半离散核矩阵K，并定义了一个连接算法G，该算法用来从K重构出原来的图形。

2.5. Graph Factorization (GF)

图因式分解（GF）应该是第一种获得O（|E|）时间复杂度的图嵌入方法。为了获得嵌入，GF对图的邻接矩阵进行因式分解，以最小化以下损失函数：

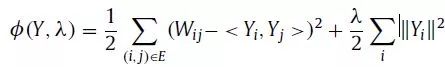
其中，λ是一个正则化系数。注意，求和是在观察到的边上，而不是所有可能的边上。这是一个考虑到可伸缩性的近似值，因此可能会在解决方案中引入噪声。注意，由于邻接矩阵通常不是半正定的，即使嵌入的维数为|v|，损失函数的最小值也大于0。

2.6. GraRep

GraRep将节点的转换概率定义为：

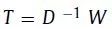
，并通过最小化来保持k阶近似，其中，

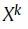
从

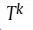
中得到（详细过程可以阅读参考文献）。然后它连接所有k的

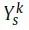
以形成

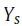
。要注意的是，这和HOPE方法很相似，HOPE通过最小化

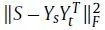
来求解，其中，S是一个合适的相似度矩阵。

GraRep的缺点是可扩展性，因为

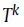
往往会有

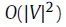
多个非零项。

2.7. HOPE

HOPE通过最小化

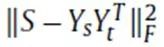
来保留更高阶的近似，其中S是相似度矩阵。HOPE的作者测试了许多不同的相似度衡量方法，包括Katz Index, Rooted Page Rank, Common Neighbors, and Adamic-Adar score，并将S定义为

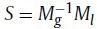
，这里面和

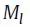
都是稀疏的，因此HOPE也可以采用常用的奇异值分解方法来获得高效的嵌入。

3、基于随机游走的方法

3.1. DeepWalk

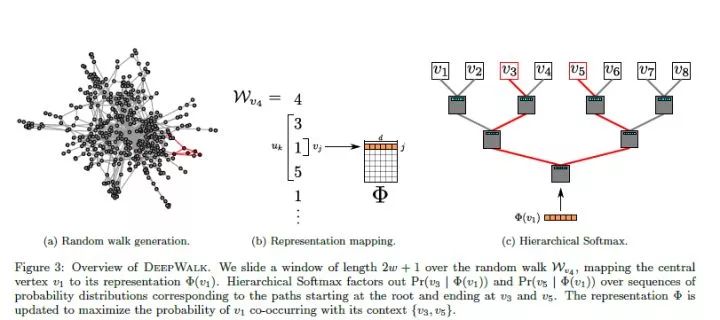
DeepWalk方法受到word2vec的启发，首先选择某一特定点为起始点，做随机游走得到点的序列，然后将这个得到的序列视为句子，用word2vec来学习，得到该点的表示向量。DeepWalk通过随机游走去可以获图中点的局部上下文信息，因此学到的表示向量反映的是该点在图中的局部结构，两个点在图中共有的邻近点（或者高阶邻近点）越多，则对应的两个向量之间的距离就越短。

3.2. node2vec

与DeepWalk相似，node2vec通过最大化随机游走得到的序列中的节点出现的概率来保持节点之间的高阶邻近性。与DeepWalk的最大区别在于，node2vec采用有偏随机游走，在广度优先（bfs）和深度优先（dfs）图搜索之间进行权衡，从而产生比DeepWalk更高质量和更多信息量的嵌入。

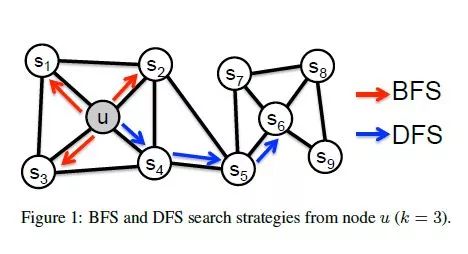
3.3. Hierarchical representation learning for networks (HARP)

DeepWalk和node2vec随机初始化节点嵌入以训练模型。由于它们的目标函数是非凸的，这种初始化很可能陷入局部最优。HARP引入了一种策略，通过更好的权重初始化来改进解决方案并避免局部最优。为此，HARP通过使用图形粗化聚合层次结构上一层中的节点来创建节点的层次结构。然后，它生成最粗糙的图的嵌入，并用所学到的嵌入初始化精炼图的节点嵌入（层次结构中的一个）。它通过层次结构传播这种嵌入，以获得原始图形的嵌入。因此，可以将HARP与基于随机行走的方法（如DeepWalk和node2vec）结合使用，以获得更好的优化函数解。

3.4. Walklets

DeepWalk和node2vec通过随机游走生成的序列，隐式地保持节点之间的高阶邻近性，由于其随机性，这些随机游走会得到不同距离的连接节点。另一方面，基于因子分解的方法，如GF和HOPE，通过在目标函数中对节点进行建模，明确地保留了节点之间的距离。Walklets将显式建模与随机游走的思想结合起来。该模型通过跳过图中的某些节点来修改DeepWalk中使用的随机游走策略。这是针对多个尺度的跳跃长度执行的，类似于在GraRep中分解

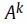
，并且随机行走获得的一组点的序列用于训练类似于DeepWalk的模型。

4、基于深度学习的方法

4.1. Structural deep network embedding (SDNE)

SDNE建议使用深度自动编码器来保持一阶和二阶网络邻近度。它通过联合优化这两个近似值来实现这一点。该方法利用高度非线性函数来获得嵌入。模型由两部分组成：无监督和监督。前者包括一个自动编码器，目的是寻找一个可以重构其邻域的节点的嵌入。后者基于拉普拉斯特征映射，当相似顶点在嵌入空间中彼此映射得很远时，该特征映射会受到惩罚。

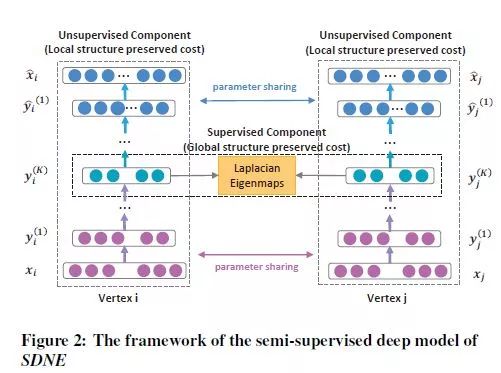
4.2. Deep neural networks for learning graph representations (DNGR)

DNGR结合了随机游走和深度自动编码器。该模型由3部分组成：随机游走、正点互信息（PPMI）计算和叠加去噪自编码器。在输入图上使用随机游走模型生成概率共现矩阵，类似于HOPE中的相似矩阵。将该矩阵转化为PPMI矩阵，输入到叠加去噪自动编码器中得到嵌入。输入PPMI矩阵保证了自动编码器模型能够捕获更高阶的近似度。此外，使用叠加去噪自动编码器有助于模型在图中存在噪声时的鲁棒性，以及捕获任务（如链路预测和节点分类）所需的底层结构。

4.3. Graph convolutional networks (GCN)

上面讨论的基于深度神经网络的方法，即SDNE和DNGR，以每个节点的全局邻域（一行DNGR的PPMI和SDNE的邻接矩阵）作为输入。对于大型稀疏图来说，这可能是一种计算代价很高且不适用的方法。图卷积网络（GCN）通过在图上定义卷积算子来解决这个问题。该模型迭代地聚合了节点的邻域嵌入，并使用在前一次迭代中获得的嵌入及其嵌入的函数来获得新的嵌入。仅局部邻域的聚合嵌入使其具有可扩展性，并且多次迭代允许学习嵌入一个节点来描述全局邻域。最近几篇论文提出了利用图上的卷积来获得半监督嵌入的方法，这种方法可以通过为每个节点定义唯一的标签来获得无监督嵌入。这些方法在卷积滤波器的构造上各不相同，卷积滤波器可大致分为空间滤波器和谱滤波器。空间滤波器直接作用于原始图和邻接矩阵，而谱滤波器作用于拉普拉斯图的谱。

4.4. Variational graph auto-encoders (VGAE)

VGAE采用了图形卷积网络（GCN）编码器和内积译码器。输入是邻接矩阵，它们依赖于GCN来学习节点之间的高阶依赖关系。他们的经验表明，与非概率自编码器相比，使用变分自编码器可以提高性能。

5、其他

LINE

LINE适用于任意类型的信息网络：无向、有向和无权、有权。该方法优化了精心设计的目标函数，能够保留局部和全局网络结构。此外，LINE中还提出了边缘采样算法，解决了经典随机梯度下降的局限性，提高了算法的有效性和效率。具体来说，LINE明确定义了两个函数，分别用于一阶和二阶近似，并最小化了这两个函数的组合。一阶邻近函数与图分解（GF）相似，都是为了保持嵌入的邻接矩阵和点积接近。区别在于GF通过直接最小化两者的差异来实现这一点。相反，LINE为每对顶点定义了两个联合概率分布，一个使用邻接矩阵，另一个使用嵌入。然后，LINE最小化了这两个分布的Kullback–Leibler（KL）散度。这两个分布和目标函数如下：

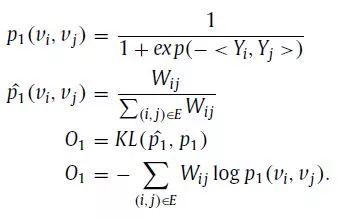
作者用和上面相似的方法定义了二阶近似的概率分布和目标函数：

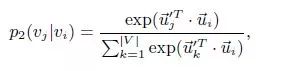
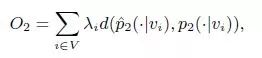
为简单起见，将λi设置为顶点i的度数，即λi= di。同样采用KL散度作为距离函数，用KL散度代替d（·，·）。再省略一些常数，得到：

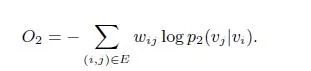
参考文献

[1] Goyal P , Ferrara E . Graph Embedding Techniques, Applications, and Performance: A Survey[J]. Knowledge-Based Systems, 2017.[2] Roweis, S. T . Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science, 2000, 290(5500):2323-2326.[3] Perozzi B , Al-Rfou R , Skiena S . DeepWalk: Online Learning of Social Representations[J]. 2014.[4] Grover A , Leskovec J . node2vec: Scalable Feature Learning for Networks[J]. Kdd, 2016.[5] Wang D , Cui P , Zhu W . Structural Deep Network Embedding[C]// the 22nd ACM SIGKDD International Conference. ACM, 2016.[6] Tang J , Qu M , Wang M , et al. LINE: Large-scale information network embedding[J]. 24th International Conference on World Wide Web, WWW 2015, 2015.