清华大学朱文武老师最新「图表示深度学习」的5种方法综述论文，51页pdf

【导读】近年来，随着网络数据量的不断增加，挖掘图形数据已成为计算机科学领域的热门研究课题，在学术界和工业界都得到了广泛的研究。但是，大量的网络数据为有效分析带来了巨大的挑战。因此激发了图表示的出现，该图表示将图映射到低维向量空间中，同时保持原始图结构并支持图推理。图的有效表示的研究具有深远的理论意义和重要的现实意义，本教程将介绍图表示/网络嵌入的一些基本思想以及一些代表性模型。

关于图或网络的文献有两个名称：图表示和网络嵌入。我们注意到图和网络都指的是同一种结构，尽管它们每个都有自己的术语，例如，图和网络的顶点和边。挖掘图/网络的核心依赖于正确表示的图/网络，这使得图/网络上的表示学习成为学术界和工业界的基本研究问题。传统表示法直接基于拓扑图来表示图，通常会导致许多问题，包括稀疏性，高计算复杂性等，从而激发了基于机器学习的方法的出现，这种方法探索了除矢量空间中的拓扑结构外还能够捕获额外信息的潜在表示。因此，对于图来说，“良好”的潜在表示可以更加精确的表示图形。但是，学习网络表示面临以下挑战：高度非线性，结构保持，属性保持，稀疏性。

深度学习在处理非线性方面的成功为我们提供了研究新方向，我们可以利用深度学习来提高图形表示学习的性能，作者在教程中讨论了将深度学习技术与图表示学习相结合的一些最新进展，主要分为两类方法：面向结构的深层方法和面向属性的深层方法。

对于面向结构的方法：

• 结构性深层网络嵌入（SDNE），专注于保持高阶邻近度。

• 深度递归网络嵌入（DRNE），其重点是维护全局结构。

• 深度超网络嵌入（DHNE），其重点是保留超结构。

对于面向属性的方法：

• 专注于不确定性属性的深度变异网络嵌入（DVNE）。

• 深度转换的基于高阶Laplacian高斯过程（DepthLGP）的网络嵌入，重点是动态属性。

本教程的第二部分就以上5种方法，通过对各个方法的模型介绍、算法介绍、对比分析等不同方面进行详细介绍。

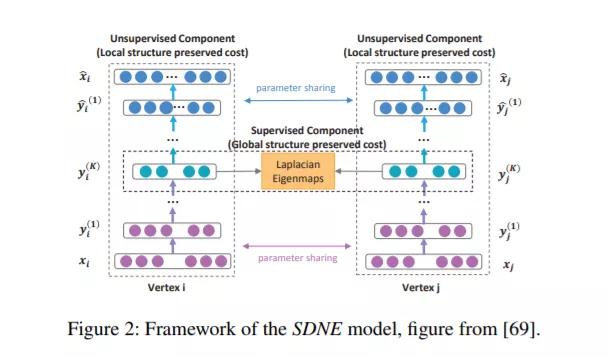
1、Structural Deep Network Embedding

network embedding，是为网络中的节点学习出一个低维表示的方法。目的在于在低维中保持高度非线性的网络结构特征，但现有方法多采用浅层网络不足以挖掘高度非线性，或同时保留局部和全局结构特征。本文提出一种结构化深度网络嵌入方法，叫SDNE该方法用半监督的深度模型来捕捉高度非线性结构，通过结合一阶相似性(监督)和二阶相似性(非监督)来保留局部和全局特征。

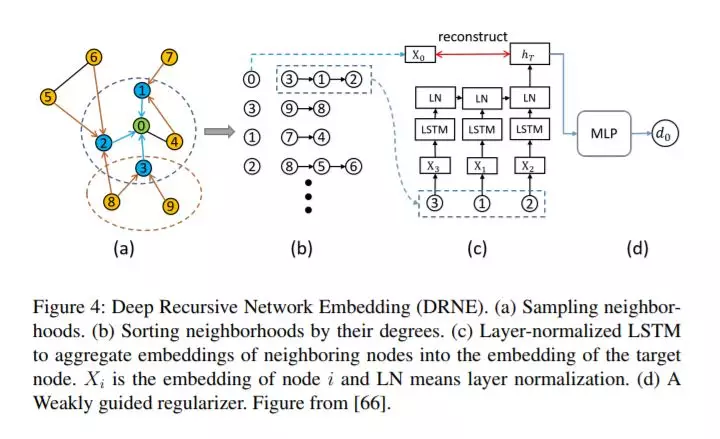
2、 Deep recursive network embedding with regular equivalence

网络嵌入旨在保留嵌入空间中的顶点相似性。现有方法通常通过节点之间的连接或公共邻域来定义相似性，即结构等效性。但是，位于网络不同部分的顶点可能具有相似的角色或位置，即规则的等价关系，在网络嵌入的文献中基本上忽略了这一点。以递归的方式定义规则对等，即两个规则对等的顶点具有也规则对等的网络邻居。因此，文章中提出了一种名为深度递归网络嵌入（DRNE）的新方法来学习具有规则等价关系的网络嵌入。更具体地说，我们提出了一种层归一化LSTM，以递归的方式通过聚合邻居的表示方法来表示每个节点。

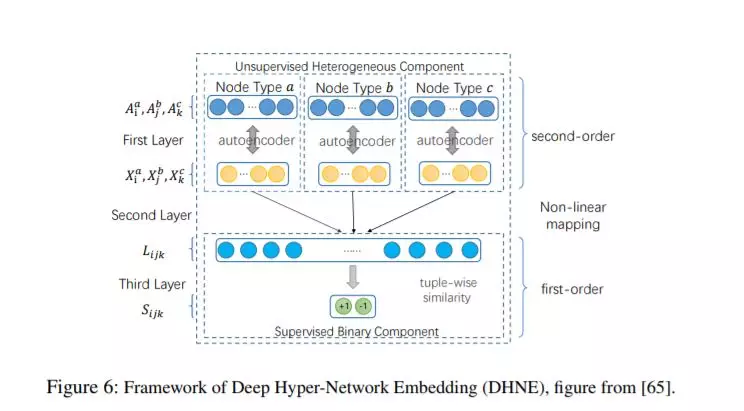
3、Structural Deep Embedding for Hyper-Networks

是在hyperedge(超边是不可分解的)的基础上保留object的一阶和二阶相似性，学习异质网络表示。于与HEBE的区别在于，本文考虑了网络high-oeder网络结构和高度稀疏性。

传统的基于clique expansion 和star expansion的方法，显式或者隐式地分解网络。也就说，分解后hyper edge节点地子集，依然可以构成一个新的超边。对于同质网络这个假设是合理地，因为同质网络地超边，大多数情况下都是根据潜在地相似性（共同地标签等）构建的。

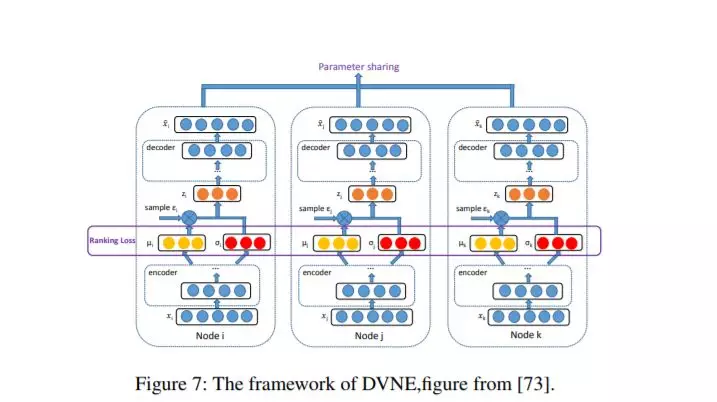
4、** Deep variational network embedding in wasserstein space**

大多数现有的嵌入方法将节点作为点向量嵌入到低维连续空间中。这样，边缘的形成是确定性的，并且仅由节点的位置确定。但是，现实世界网络的形成和发展充满不确定性，这使得这些方法不是最优的。为了解决该问题，在本文中提出了一种新颖的在Wasserstein空间中嵌入深度变分网络（DVNE）。所提出的方法学习在Wasserstein空间中的高斯分布作为每个节点的潜在表示，它可以同时保留网络结构并为节点的不确定性建模。具体来说，我们使用2-Wasserstein距离作为分布之间的相似性度量，它可以用线性计算成本很好地保留网络中的传递性。此外，我们的方法通过深度变分模型隐含了均值和方差的数学相关性，可以通过均值矢量很好地捕获节点的位置，而由方差可以很好地捕获节点的不确定性。此外，本文方法通过保留网络中的一阶和二阶邻近性来捕获局部和全局网络结构。

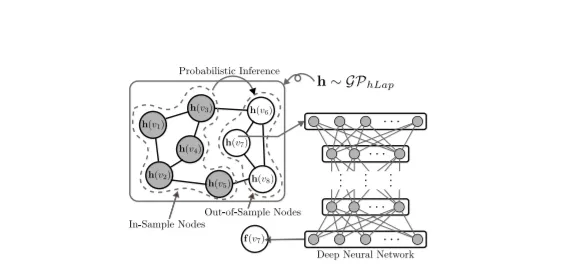
5、Learning embeddings of out-of-sample nodes in dynamic networks

迄今为止的网络嵌入算法主要是为静态网络设计的，在学习之前，所有节点都是已知的。如何为样本外节点（即学习后到达的节点）推断嵌入仍然是一个悬而未决的问题。该问题对现有方法提出了很大的挑战，因为推断的嵌入应保留复杂的网络属性，例如高阶邻近度，与样本内节点嵌入具有相似的特征（即具有同质空间），并且计算成本较低。为了克服这些挑战，本文提出了一种深度转换的高阶拉普拉斯高斯过程（DepthLGP）方法来推断样本外节点的嵌入。DepthLGP结合了非参数概率建模和深度学习的优势。特别是，本文设计了一个高阶Laplacian高斯过程（hLGP）来对网络属性进行编码，从而可以进行快速和可扩展的推理。为了进一步确保同质性，使用深度神经网络来学习从hLGP的潜在状态到节点嵌入的非线性转换。DepthLGP是通用的，因为它适用于任何网络嵌入算法学习到的嵌入。