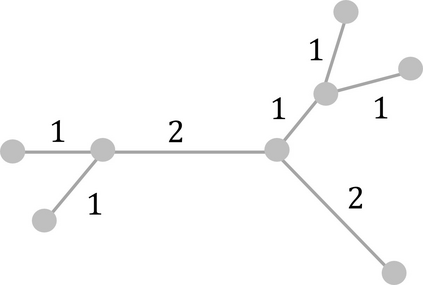
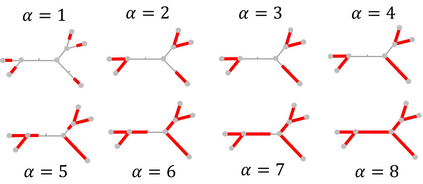
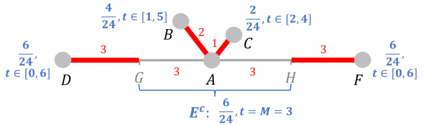
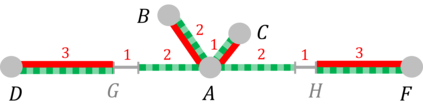
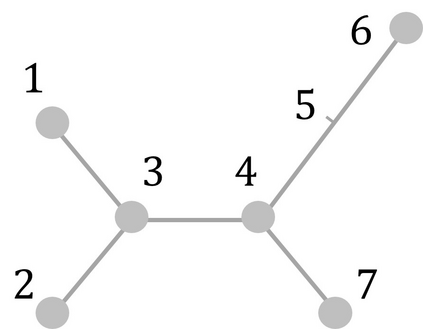
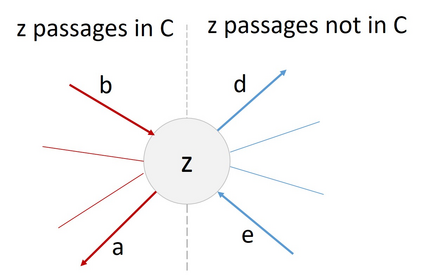
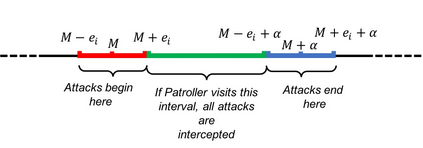
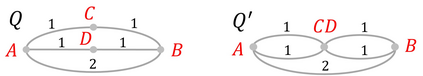We study a patrolling game played on a network $Q$, considered as a metric space. The Attacker chooses a point of $Q$ (not necessarily a node) to attack during a chosen time interval of fixed duration. The Patroller chooses a unit speed path on $Q$ and intercepts the attack (and wins) if she visits the attacked point during the attack time interval. This zero-sum game models the problem of protecting roads or pipelines from an adversarial attack. The payoff to the maximizing Patroller is the probability that the attack is intercepted. Our results include the following: (i) a solution to the game for any network $Q$, as long as the time required to carry out the attack is sufficiently short, (ii) a solution to the game for all tree networks that satisfy a certain condition on their extremities, and (iii) a solution to the game for any attack duration for stars with one long arc and the remaining arcs equal in length. We present a conjecture on the solution of the game for arbitrary trees and establish it in certain cases.
翻译:我们研究在网络上玩的巡逻游戏$Q, 被视为一个公制空间。 攻击者选择了一个在固定时间间隔内攻击的点为$Q( 不一定是一个节点) 。 巡逻员选择了以$为单位的速度路径, 如果在攻击时间间隔内访问攻击点, 则拦截攻击( 赢 ) 。 这种零和游戏模式是保护道路或管道不受对抗性攻击的问题 。 对最大化巡逻员的回报是袭击被拦截的概率 。 我们的结果包括以下内容:( 一) 只要攻击所需的时间足够短, 任何网络的游戏的解决方案 $Q, 只要进行攻击所需的时间足够短, (二) 所有树木网络的游戏解决方案, 只要其外观满足一定条件, 并且 (三) 以长弧和剩余弧长度相等的恒星的任何攻击时间的游戏的解决方案 。 我们对任意树木的游戏的解决方案进行猜测, 并在特定情况下建立游戏 。
相关内容
Source: Apple - iOS 8