Universal Bootstrap for Spectral Statistics: Beyond Gaussian Approximation

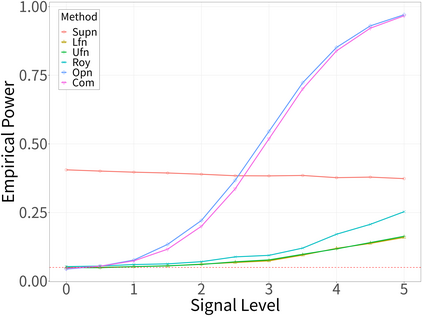
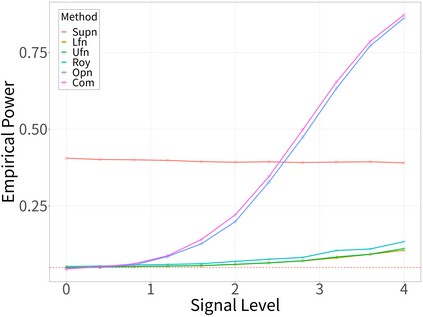
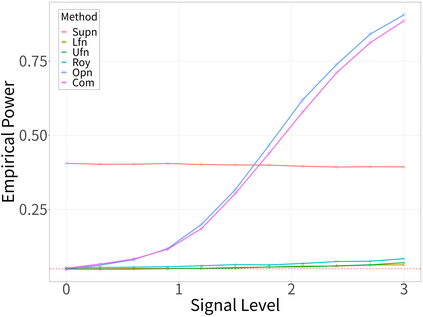
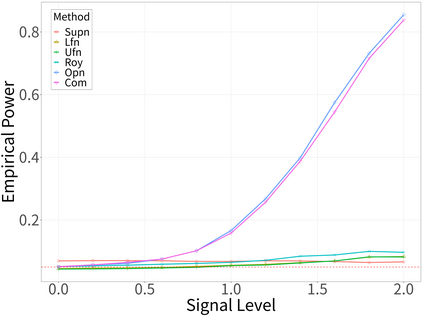
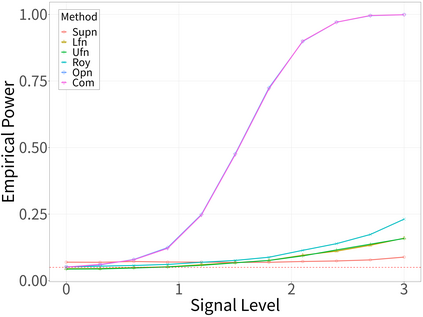
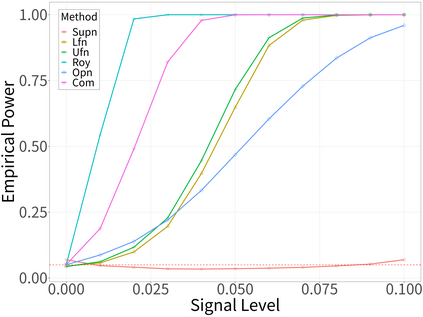
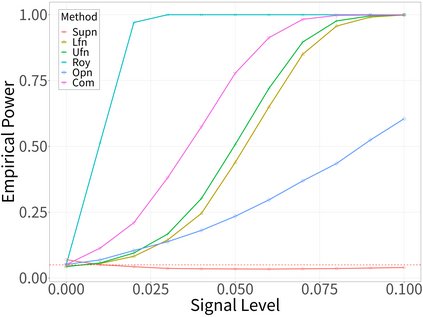
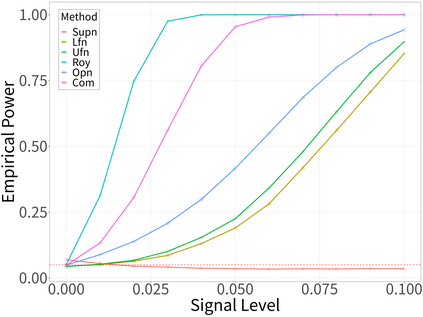
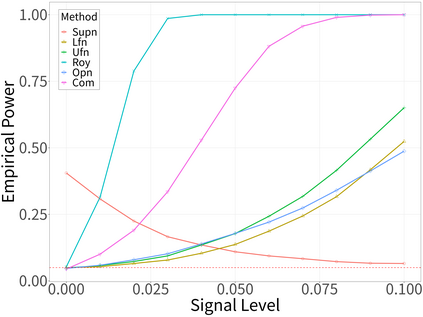
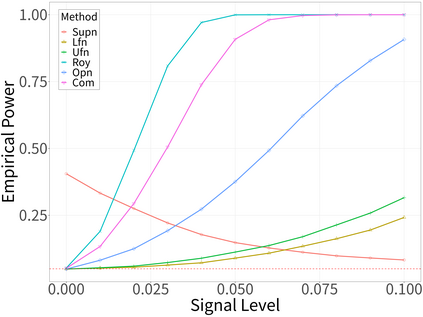
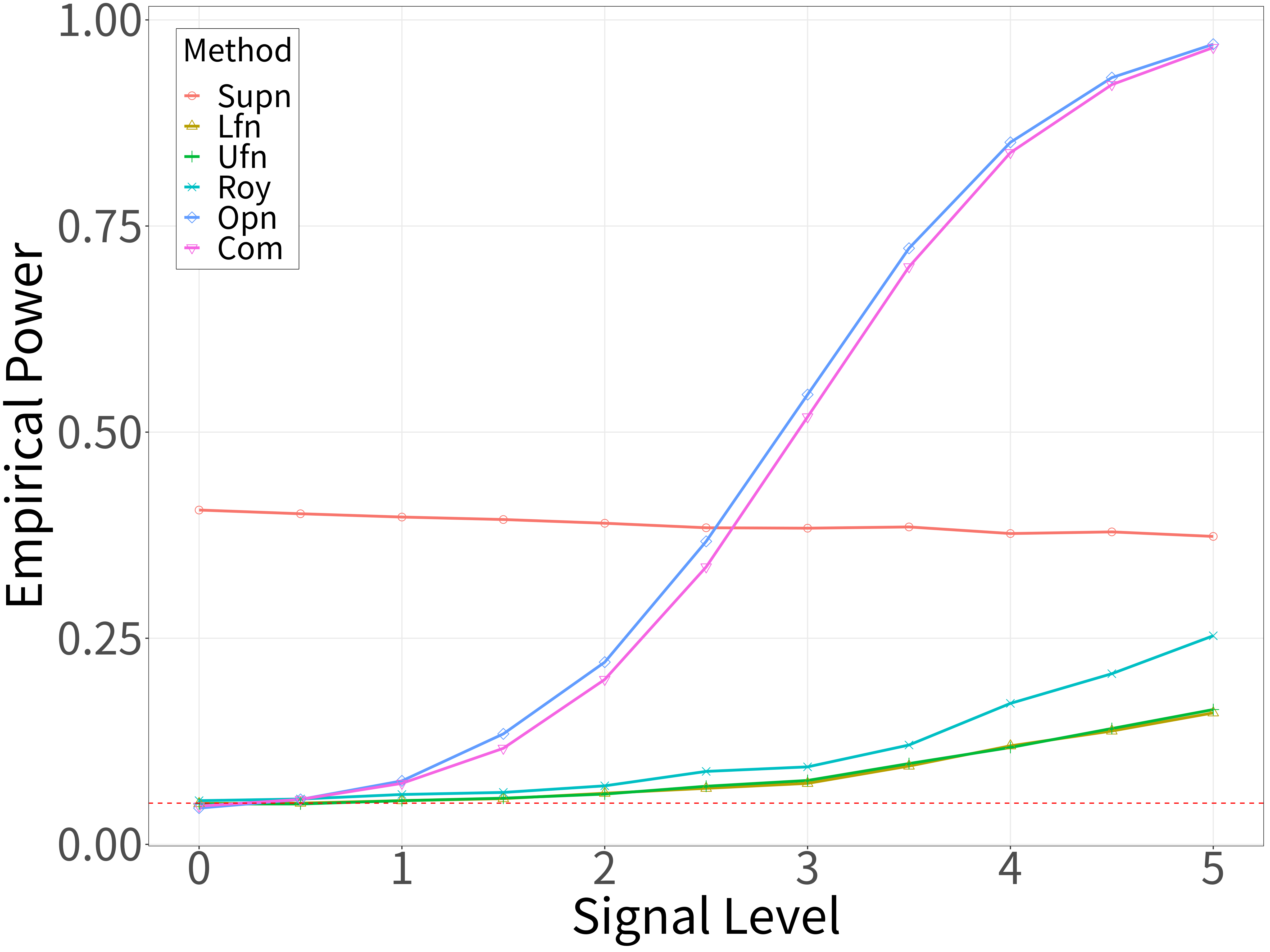
Spectral analysis plays a crucial role in high-dimensional statistics, where determining the asymptotic distribution of various spectral statistics remains a challenging task. Due to the difficulties of deriving the analytic form, recent advances have explored data-driven bootstrap methods for this purpose. However, widely used Gaussian approximation-based bootstrap methods, such as the empirical bootstrap and multiplier bootstrap, have been shown to be inconsistent in approximating the distributions of spectral statistics in high-dimensional settings. To address this issue, we propose a universal bootstrap procedure based on the concept of universality from random matrix theory. Our method consistently approximates a broad class of spectral statistics across both high- and ultra-high-dimensional regimes, accommodating scenarios where the dimension-to-sample-size ratio $p/n$ converges to a nonzero constant or diverges to infinity without requiring structural assumptions on the population covariance matrix, such as eigenvalue decay or low effective rank. We showcase this universal bootstrap method for high-dimensional covariance inference. Extensive simulations and a real-world data study support our findings, highlighting the favorable finite sample performance of the proposed universal bootstrap procedure.