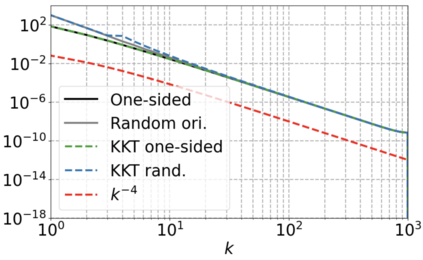
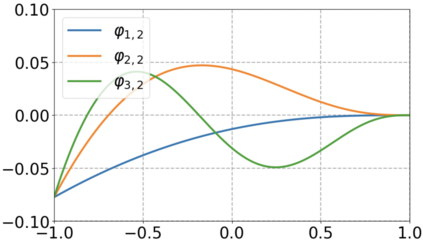
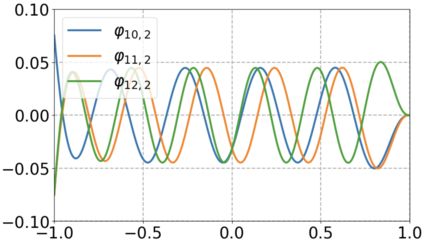
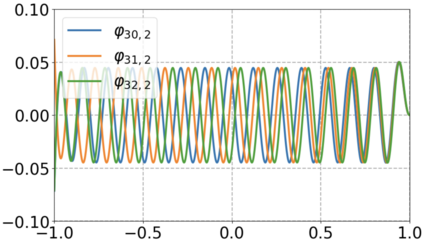
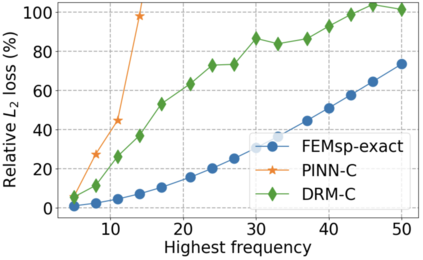
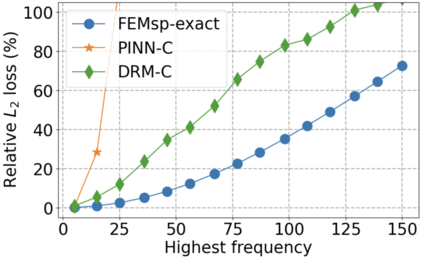
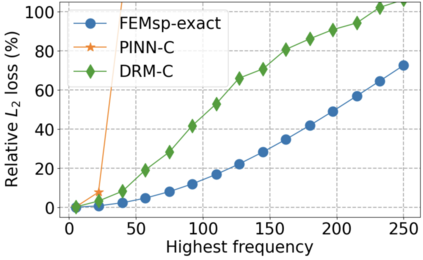
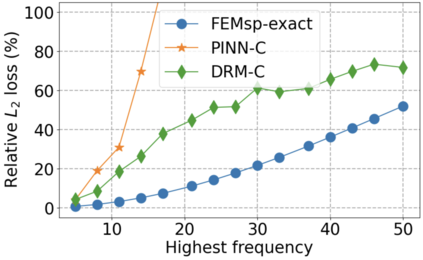
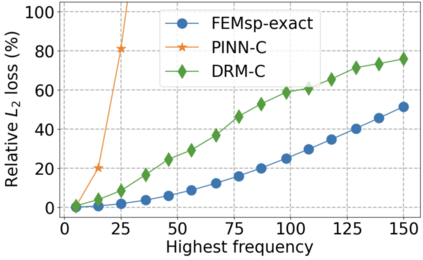
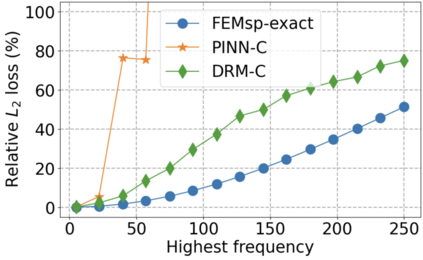
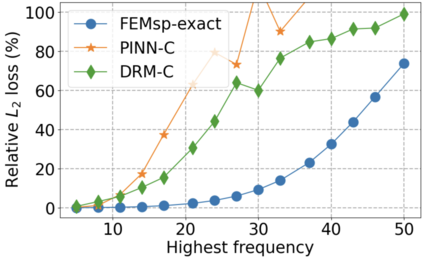
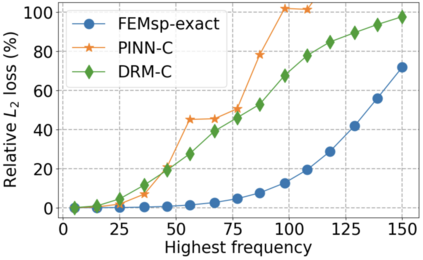
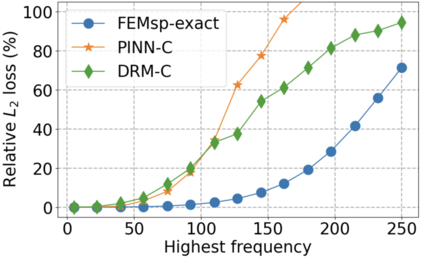
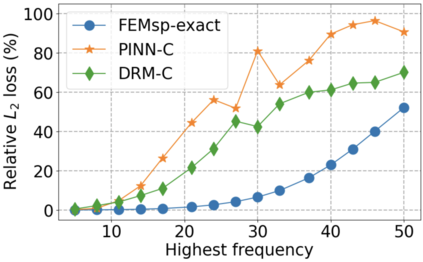
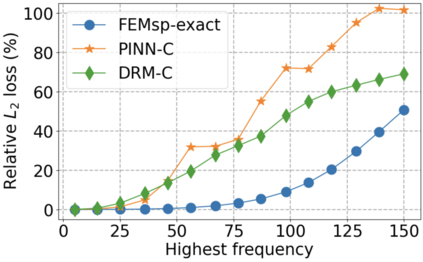
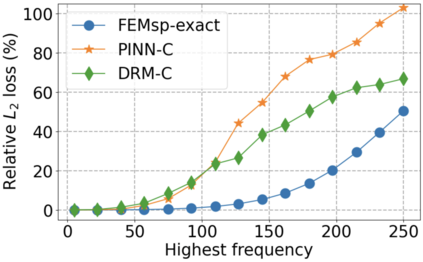
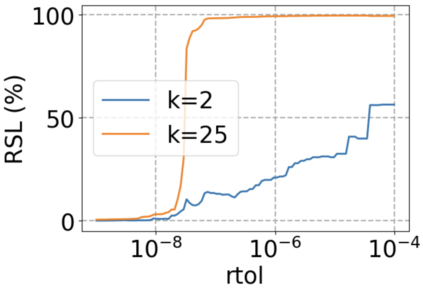
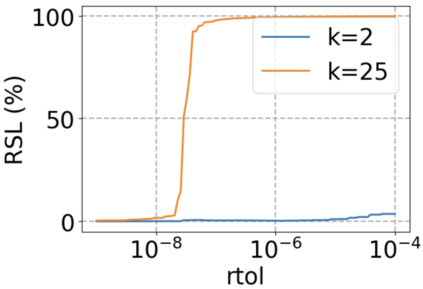
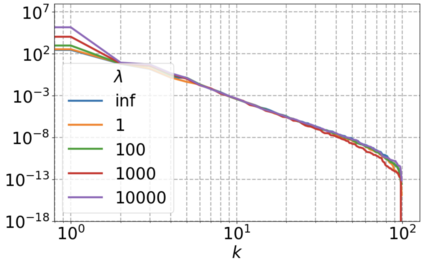
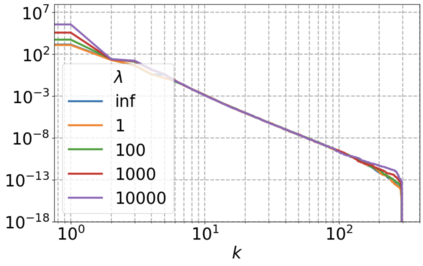
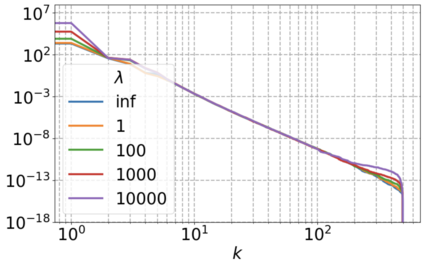
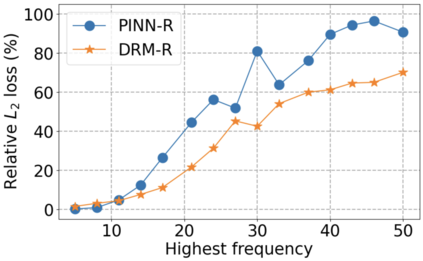
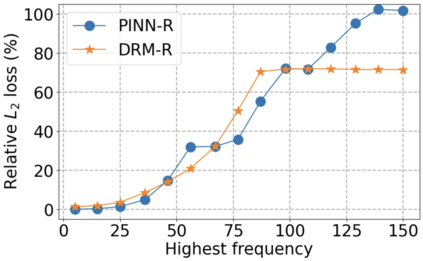
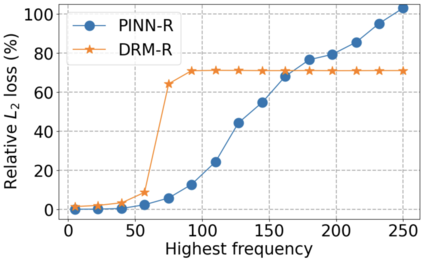
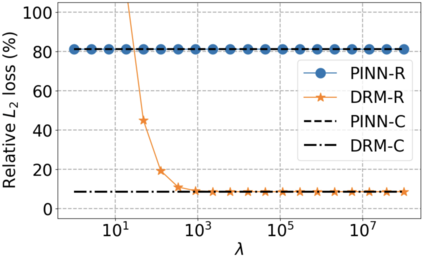
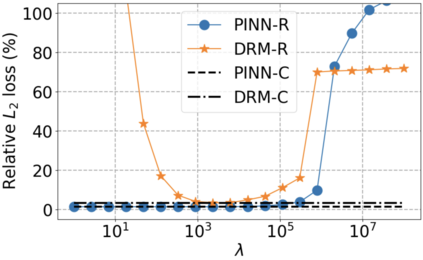
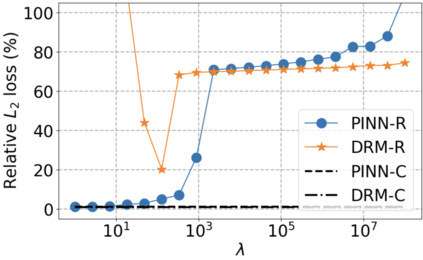
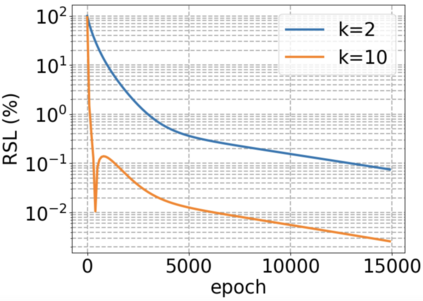
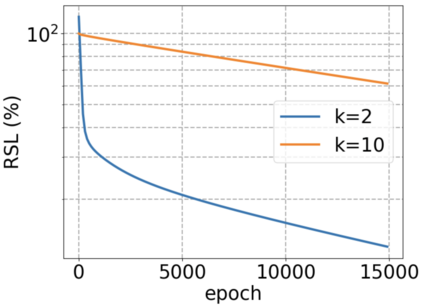
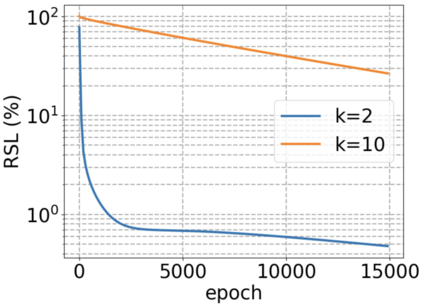
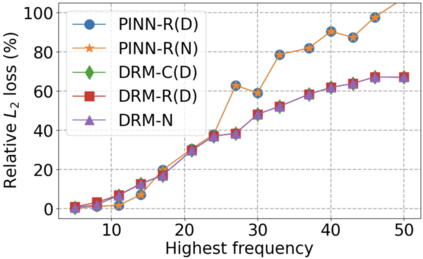
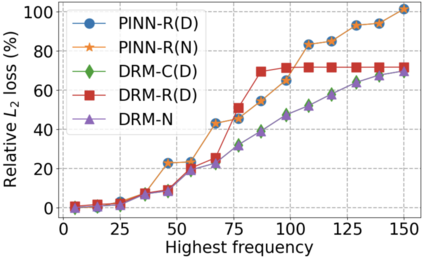
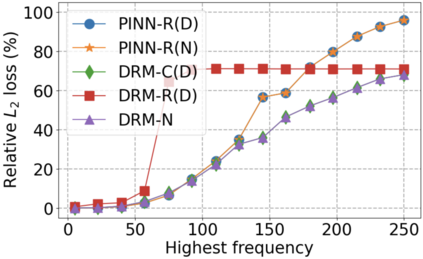
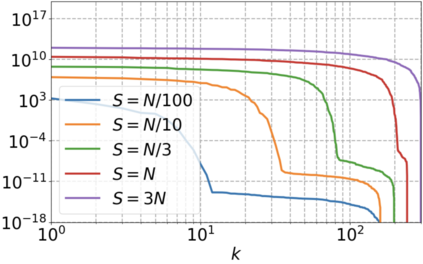
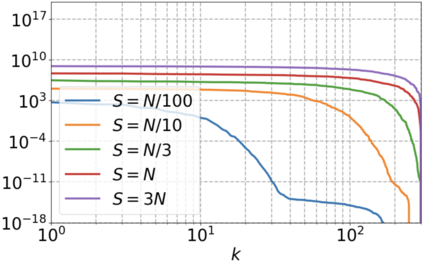
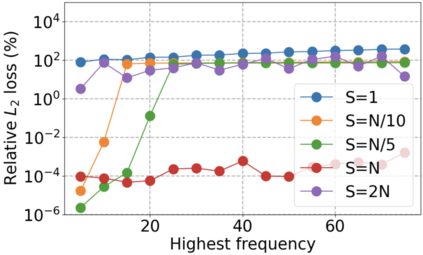
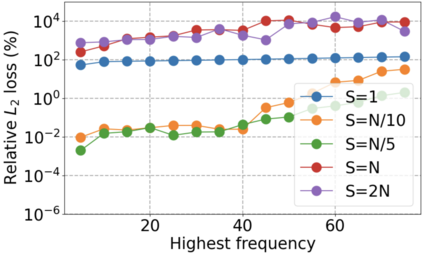
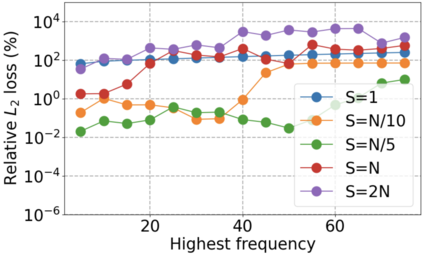
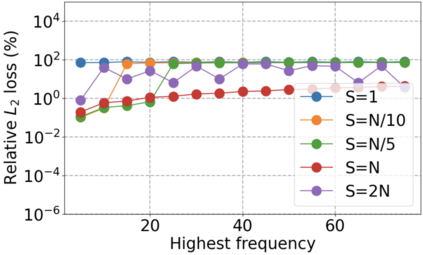
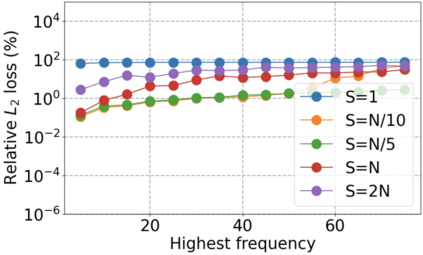
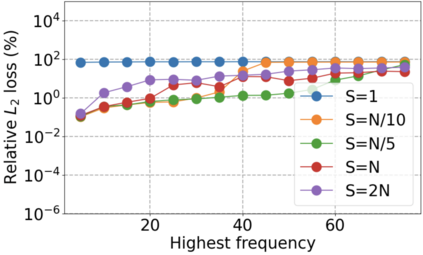
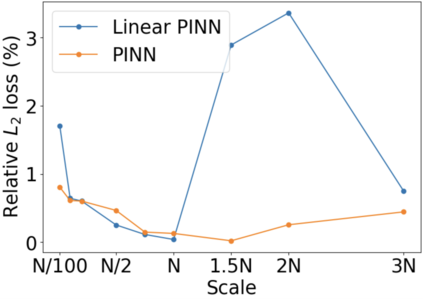
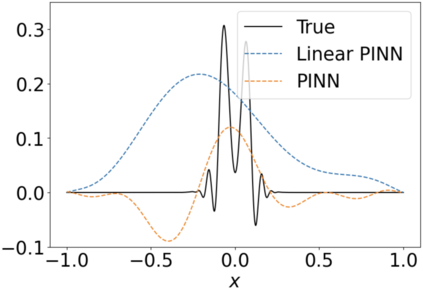
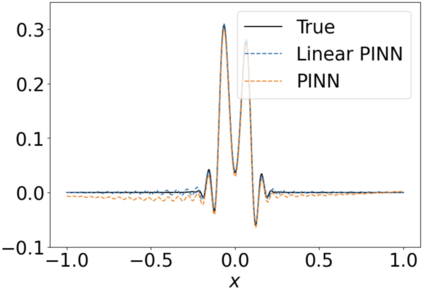
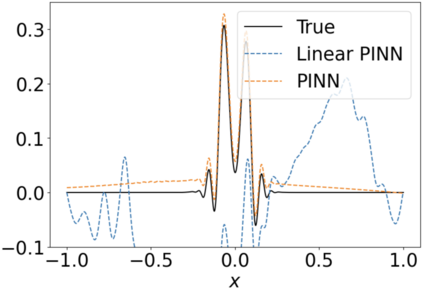
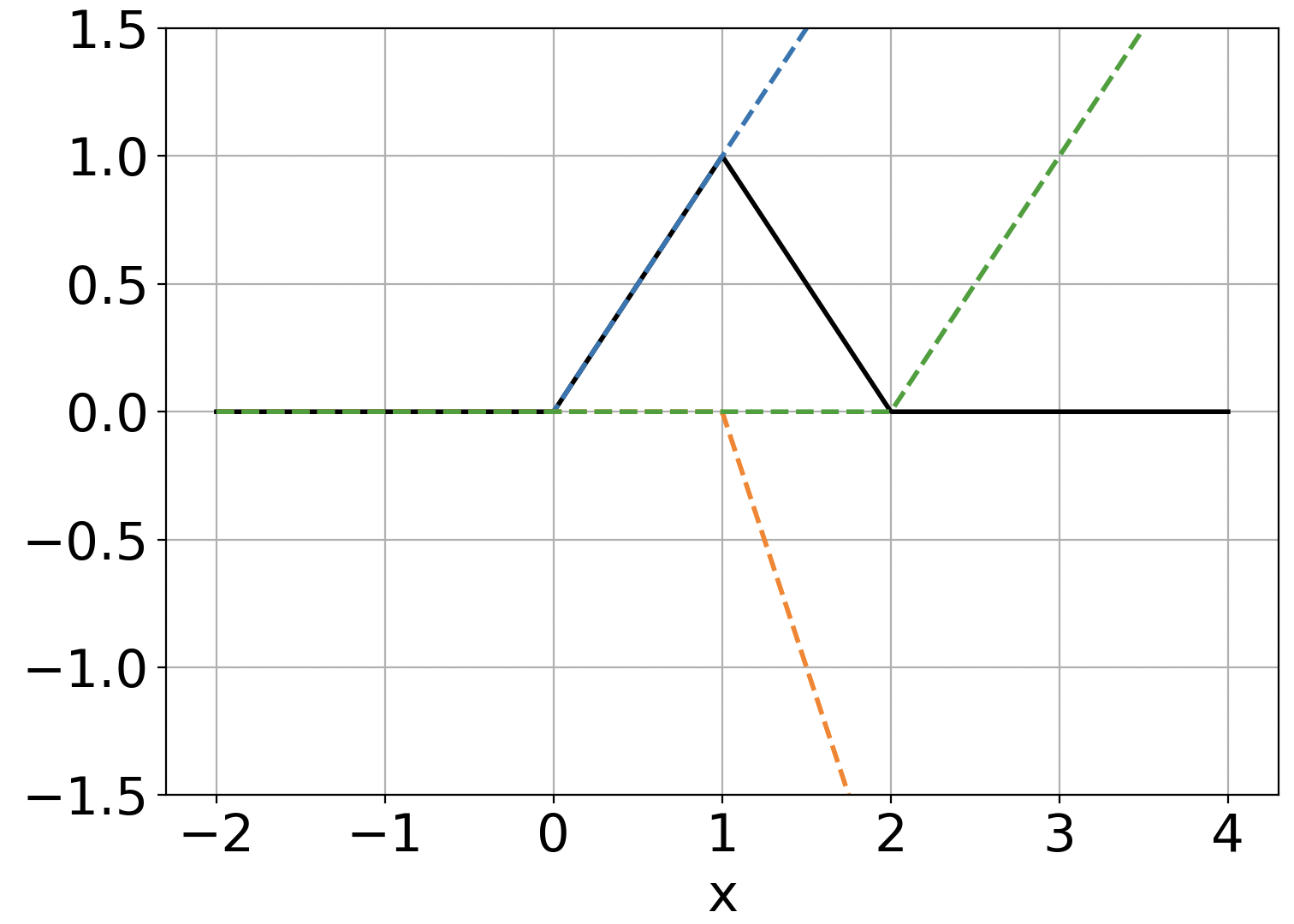
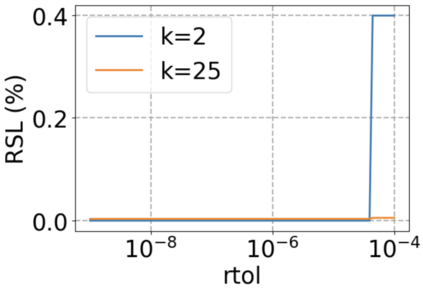We use elliptic partial differential equations (PDEs) as examples to show various properties and behaviors when shallow neural networks (SNNs) are used to represent the solutions. In particular, we study the numerical ill-conditioning, frequency bias, and the balance between the differential operator and the shallow network representation for different formulations of the PDEs and with various activation functions. Our study shows that the performance of Physics-Informed Neural Networks (PINNs) or Deep Ritz Method (DRM) using linear SNNs with power ReLU activation is dominated by their inherent ill-conditioning and spectral bias against high frequencies. Although this can be alleviated by using non-homogeneous activation functions with proper scaling, achieving such adaptivity for nonlinear SNNs remains costly due to ill-conditioning.
翻译:暂无翻译