On the determination of Lagrange Multipliers for a weighted LASSO problem using geometric and convex analysis techniques

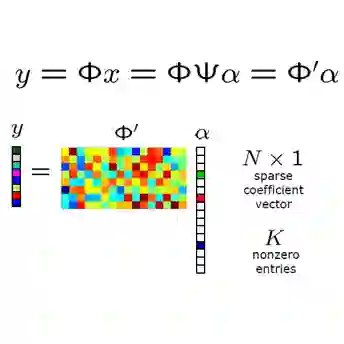
Compressed Sensing (CS) encompasses a broad array of theoretical and applied techniques for recovering signals, given partial knowledge of their coefficients. Its applications span various fields, including mathematics, physics, engineering, and several medical sciences. Motivated by our interest in the mathematics behind Magnetic Resonance Imaging (MRI) and CS, we employ convex analysis techniques to analytically determine equivalents of Lagrange multipliers for optimization problems with inequality constraints, specifically a weighted LASSO with voxel-wise weighting. We investigate this problem under assumptions on the fidelity term $\Vert{Ax-b}\Vert_2^2$, either concerning the sign of its gradient or orthogonality-like conditions of its matrix. To be more precise, we either require the sign of each coordinate of $2(Ax-b)^TA$ to be fixed within a rectangular neighborhood of the origin, with the side lengths of the rectangle dependent on the constraints, or we assume $A^TA$ to be diagonal. The objective of this work is to explore the relationship between Lagrange multipliers and the constraints of a weighted variant of LASSO, specifically in the mentioned cases where this relationship can be computed explicitly. As they scale the regularization terms of the weighted LASSO, Lagrange multipliers serve as tuning parameters for the weighted LASSO, prompting the question of their potential effective use as tuning parameters in applications like MR image reconstruction and denoising. This work represents an initial step in this direction.