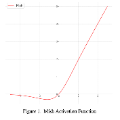
Activation functions are the linchpins of deep learning, profoundly influencing both the representational capacity and training dynamics of neural networks. They shape not only the nature of representations but also optimize convergence rates and enhance generalization potential. Appreciating this critical role, we present the Linear Oscillation (LoC) activation function, defined as $f(x) = x \times \sin(\alpha x + \beta)$. Distinct from conventional activation functions which primarily introduce non-linearity, LoC seamlessly blends linear trajectories with oscillatory deviations. The nomenclature "Linear Oscillation" is a nod to its unique attribute of infusing linear activations with harmonious oscillations, capturing the essence of the "Importance of Confusion". This concept of "controlled confusion" within network activations is posited to foster more robust learning, particularly in contexts that necessitate discerning subtle patterns. Our empirical studies reveal that, when integrated into diverse neural architectures, the LoC activation function consistently outperforms established counterparts like ReLU and Sigmoid. The stellar performance exhibited by the avant-garde Vision Transformer model using LoC further validates its efficacy. This study illuminates the remarkable benefits of the LoC over other prominent activation functions. It champions the notion that intermittently introducing deliberate complexity or "confusion" during training can spur more profound and nuanced learning. This accentuates the pivotal role of judiciously selected activation functions in shaping the future of neural network training.
翻译:暂无翻译