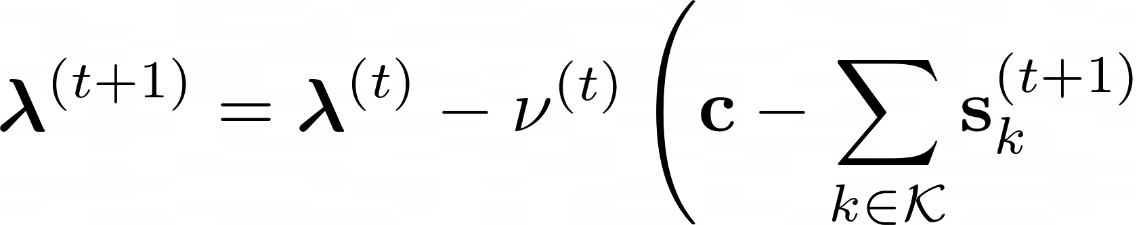Differential Privacy in Multi-Party Resource Sharing

This study examines a resource-sharing problem involving multiple parties that agree to use a set of capacities together. We start with modeling the whole problem as a mathematical program, where all parties are required to exchange information to obtain the optimal objective function value. This information bears private data from each party in terms of coefficients used in the mathematical program. Moreover, the parties also consider the individual optimal solutions as private. In this setting, the concern for the parties is the privacy of their data and their optimal allocations. We propose a two-step approach to meet the privacy requirements of the parties. In the first step, we obtain a reformulated model that is amenable to a decomposition scheme. Although this scheme eliminates almost all data exchange, it does not provide a formal privacy guarantee. In the second step, we provide this guarantee with a differentially private algorithm at the expense of deviating slightly from the optimality. We provide bounds on this deviation and discuss the consequences of these theoretical results. We also propose a novel modification to increase the efficiency of the algorithm in terms of reducing the theoretical optimality gap. The study ends with a numerical experiment on a planning problem that demonstrates an application of the proposed approach. As we work with a general optimization model, our analysis and discussion can be used in different application areas including production planning, logistics, and network revenue management.