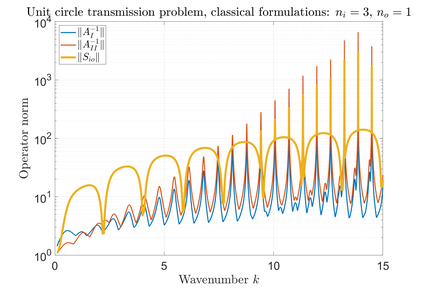
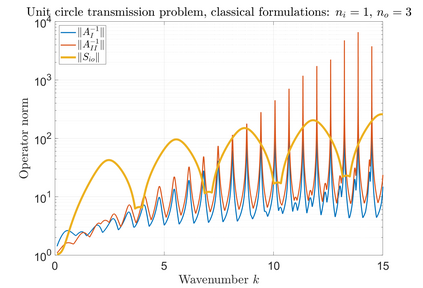
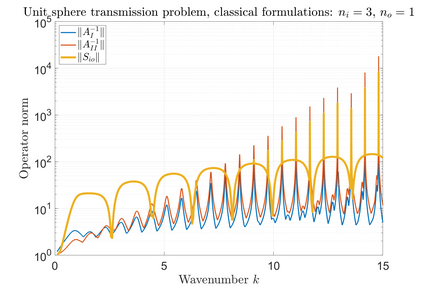
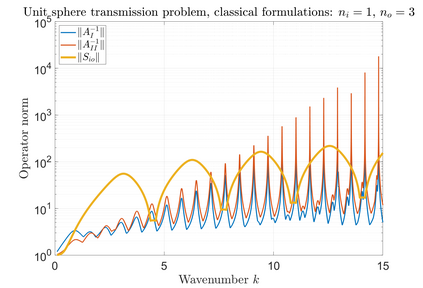
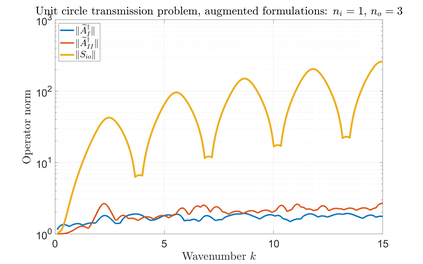
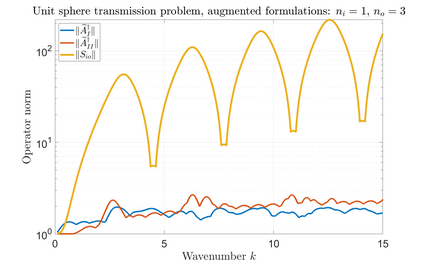
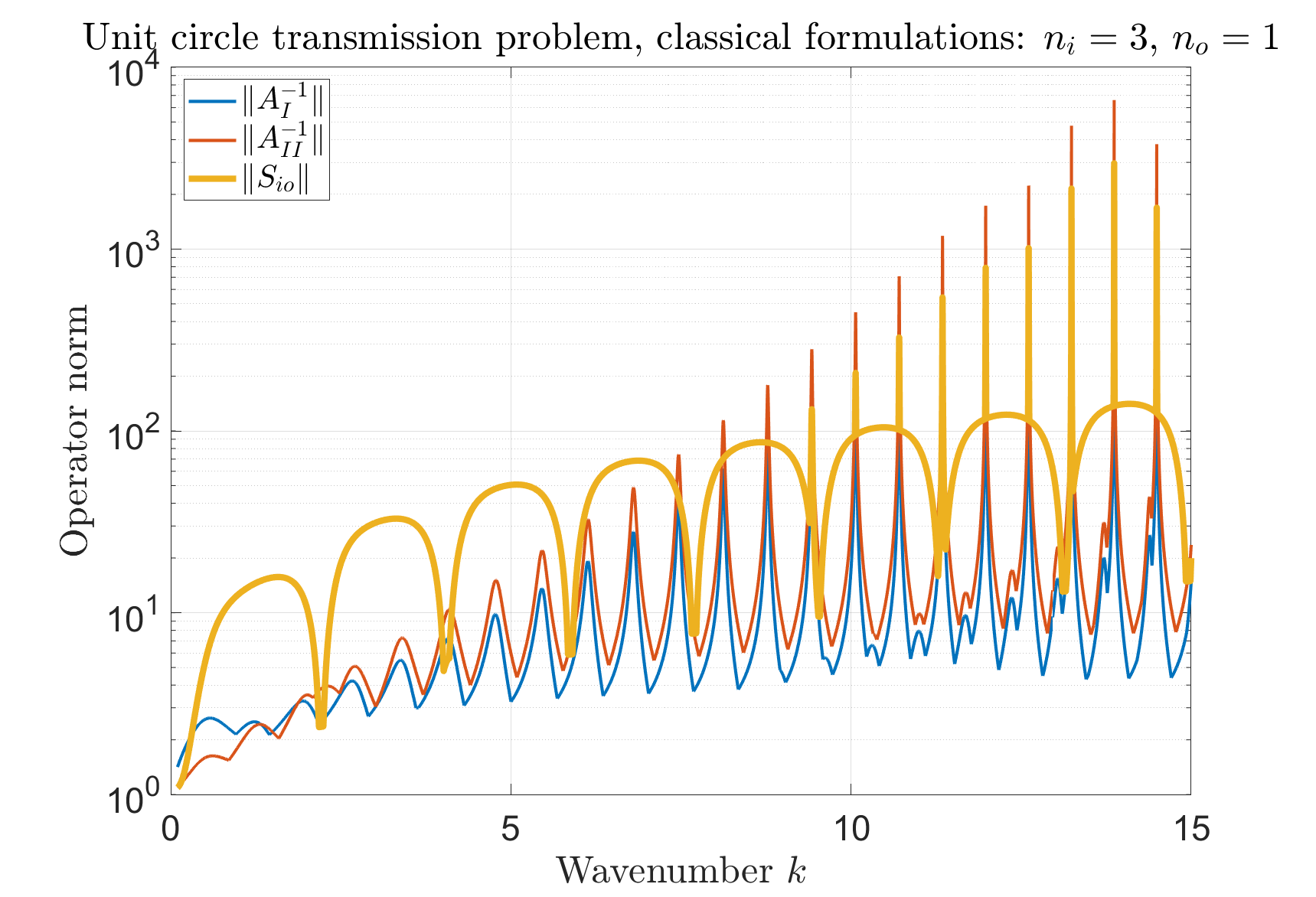
We consider the Helmholtz transmission problem with piecewise-constant material coefficients, and the standard associated direct boundary integral equations. For certain coefficients and geometries, the norms of the inverses of the boundary integral operators grow rapidly through an increasing sequence of frequencies, even though this is not the case for the solution operator of the transmission problem; we call this phenomenon that of spurious quasi-resonances. We give a rigorous explanation of why and when spurious quasi-resonances occur, and propose modified boundary integral equations that are not affected by them.
翻译:我们认为赫尔姆霍尔茨传输问题涉及片断物质系数和标准的相关直接边界等分法。 对于某些系数和几何方程式,边界一体化操作者反面的规范随着频率的增加而迅速增长,尽管对于传输问题的解决者来说情况并非如此;我们称之为虚假的准共性现象。我们严格解释为什么和何时出现虚假的准共性,并提出不受其影响的经修改的边界一体化方程式。