High Probability Lower Bounds for the Total Variation Distance

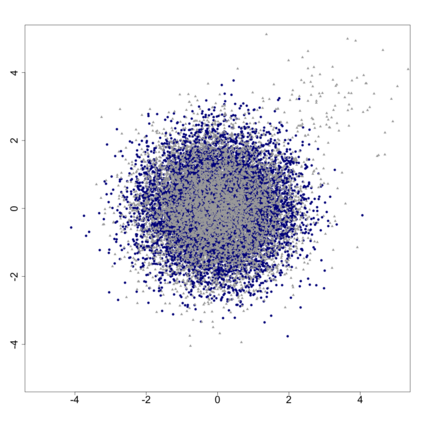
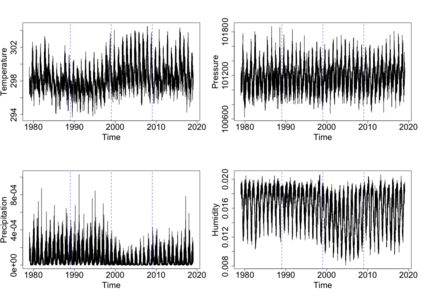
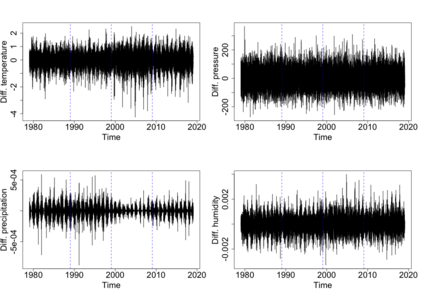
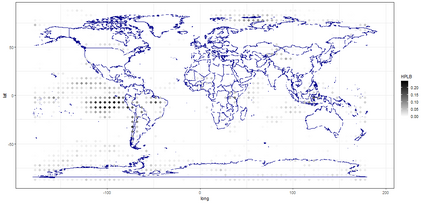
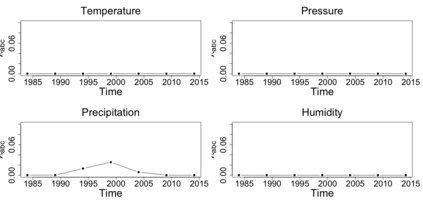
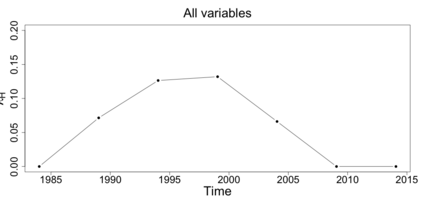
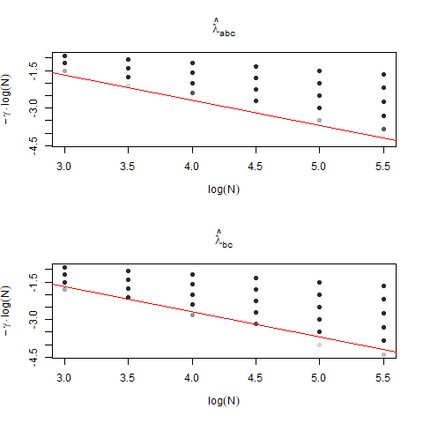
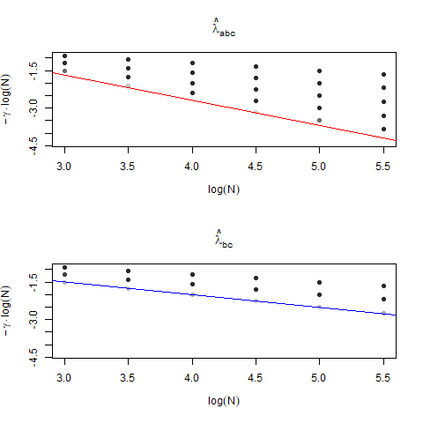
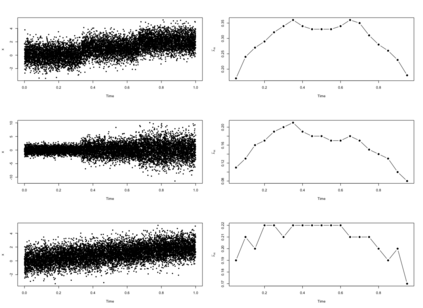
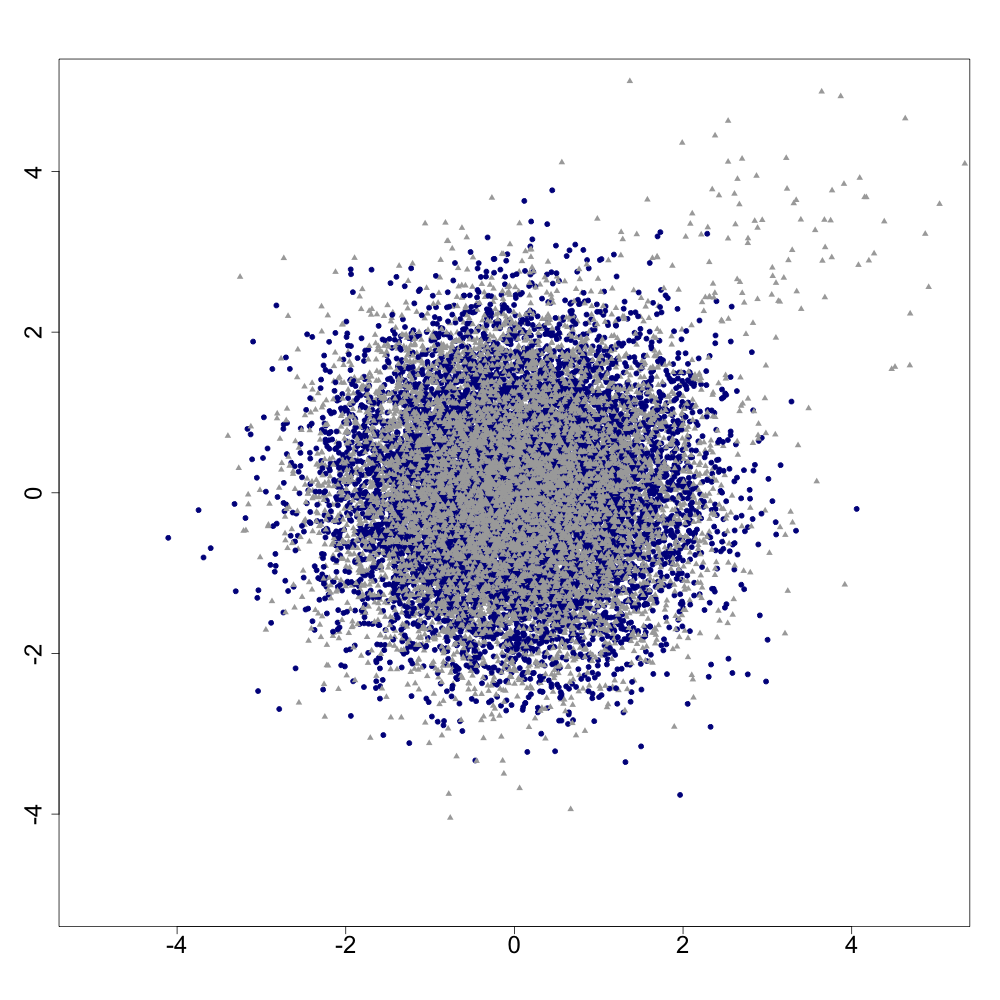
The statistics and machine learning communities have recently seen a growing interest in classification-based approaches to two-sample testing (e.g. Kim et al. [2016]; Rosenblatt et al. [2016]; Lopez-Paz and Oquab [2017]; Hediger et al. [2019]). The outcome of a classification-based two-sample test remains a rejection decision, which is not always informative since the null hypothesis is seldom strictly true. Therefore, when a test rejects, it would be beneficial to provide an additional quantity serving as a refined measure of distributional difference. In this work, we introduce a framework for the construction of high-probability lower bounds on the total variation distance. These bounds are based on a one-dimensional projection, such as a classification or regression method, and can be interpreted as the minimal fraction of samples pointing towards a distributional difference. We further derive asymptotic power and detection rates of two proposed estimators and discuss potential uses through an application to a reanalysis climate dataset.