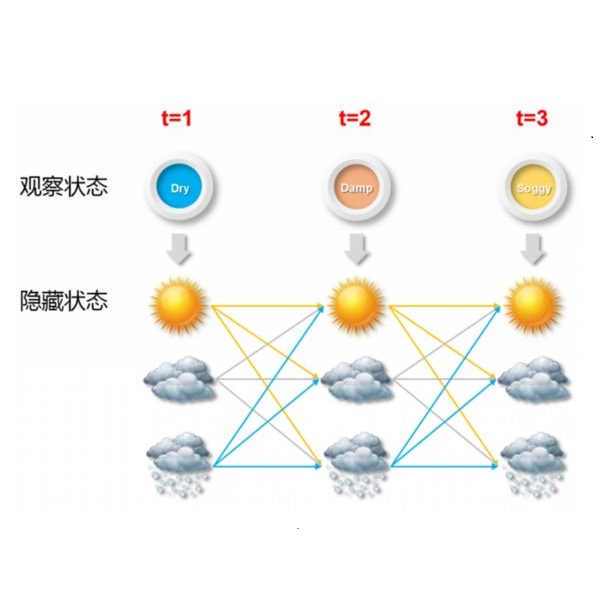
We study the frontier between learnable and unlearnable hidden Markov models (HMMs). HMMs are flexible tools for clustering dependent data coming from unknown populations. The model parameters are known to be fully identifiable (up to label-switching) without any modeling assumption on the distributions of the populations as soon as the clusters are distinct and the hidden chain is ergodic with a full rank transition matrix. In the limit as any one of these conditions fails, it becomes impossible in general to identify parameters. For a chain with two hidden states we prove nonasymptotic minimax upper and lower bounds, matching up to constants, which exhibit thresholds at which the parameters become learnable. We also provide an upper bound on the relative entropy rate for parameters in a neighbourhood of the unlearnable region which may have interest in itself.
翻译:我们研究了可学习和不可遗漏的隐性Markov模型(HMMs)之间的边框。 HMMs是将来自未知人群的依附数据分组的灵活工具。 模型参数已知完全可以识别( 直至标签开动), 而当聚群分辨, 隐藏链与完整级过渡矩阵发生性关系时, 模型参数的分布没有任何模型假设。 在任何一种条件都失败的极限下, 通常都无法确定参数。 对于两个隐藏状态的链条, 我们证明, 与常数相匹配, 常数显示参数可以学习的阈值。 我们还为可能具有自身利益的不可转移区域附近的参数提供了相对导值的上限。